文章目录
- 一：牛顿法 （Newton's method）
- 1：概述
- 2：牛顿方向与牛顿法
- 3：牛顿法的基本步骤
- 4：举例
- 二：高斯牛顿法 （Gauss–Newton algorithm）
- 1：概述
- 2：高斯牛顿法推导
- 3：高斯牛顿法算法流程
- 4：高斯牛顿法 C++ 代码
- 三：列文伯格-马夸尔特法（Levenberg-Marquardt algorithm）
- 1：概述
- 2：LM算法流程
- 3：列文伯格-马夸尔特法 C++ 代码
- 四：总结
个人笔记：
牛顿(Newton) 法、高斯牛顿(GaussNewton)法、Levenberg-Marquardt(LM)算法等。结合自己需要实现功能的目的，下面主要给出推导结果、代码实现和实际一些应用。推导过程最后会放一些个人参考的一些文章和资料。
一：牛顿法 （Newton’s method）
1：概述
牛顿法是一种函数逼近法,它的基本思想是：在极小点附近用
x
(
k
)
x^{(k)}
x(k)点的二阶泰勒多项式来近似目标函数
f
(
x
)
f(x)
f(x),并用选代点
x
(
k
)
x^{(k)}
x(k)处指向近似二次函数的极小点方向作为搜索方向
p
(
k
)
p^{(k)}
p(k)。
设规划问题 ：
m
i
n
f
(
x
)
,
x
∈
R
n
min f(x),x∈R^n
minf(x),x∈Rn
其中
f
(
x
)
f(x)
f(x)在点
x
(
k
)
x^{(k)}
x(k)处具有二阶连续偏导数,黑森矩阵
▽
2
f
(
x
(
k
)
)
▽^2f(x^{(k)})
▽2f(x(k))正定。
现已有
f
(
x
)
f(x)
f(x)极小点的第
k
k
k级估计值
x
(
k
)
x^{(k)}
x(k),并将
f
(
x
)
f(x)
f(x)作二阶泰勒展开:
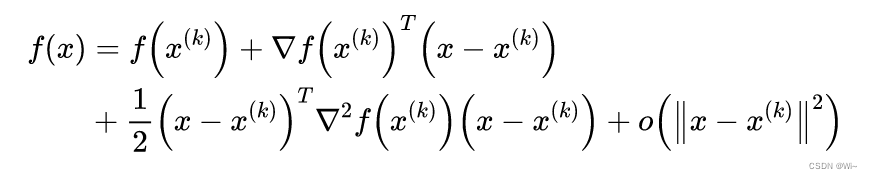其中主要的是前三项，最后一项为高阶无穷小。
2：牛顿方向与牛顿法
记上式中的主要部分为：
在
x
(
k
)
x^{(k)}
x(k)附近可用
Q
(
x
)
Q(x)
Q(x)来近似
f
(
x
)
f(x)
f(x),
Q
(
x
)
≈
f
(
x
)
Q(x) ≈ f(x)
Q(x)≈f(x)。
故可以用
Q
(
x
)
Q(x)
Q(x)的极小点来近似
f
(
x
)
f(x)
f(x)的极小点,求
Q
(
x
)
Q(x)
Q(x)的驻点：
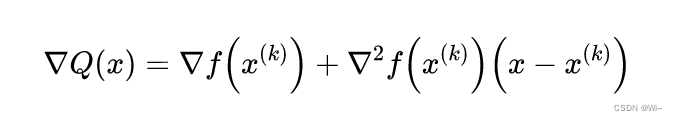
由梯度 ▽ Q ( x ) = 0 ▽Q(x) = 0 ▽Q(x)=0得 Q ( x ) Q(x) Q(x)的平稳点 x ( k + 1 ) x^{(k+1)} x(k+1)， p ( k ) p^{(k)} p(k)是牛顿方向，步长为 1 1 1
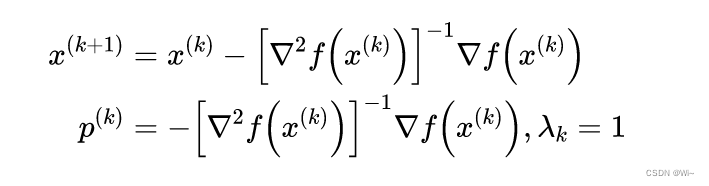
也就是下面描述，其中
H
H
H是黑塞矩阵
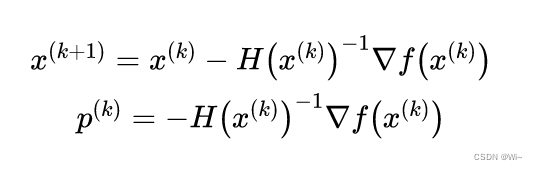
3：牛顿法的基本步骤
1：选取初始数据：初始点
x
(
0
)
x^{(0)}
x(0),终止条件
ε
>
0
ε>0
ε>0，令
k
:
=
0
k:=0
k:=0
2：求梯度向量
▽
f
(
k
)
▽f^{(k)}
▽f(k),并计算
∣
∣
▽
f
(
k
)
∣
∣
||▽f^{(k)}||
∣∣▽f(k)∣∣:
若 ∣ ∣ ▽ f ( k ) ∣ ∣ < ε ||▽f^{(k)}||<ε ∣∣▽f(k)∣∣<ε,停止选代,输出 x ( k ) x^{(k)} x(k),否则转下一步。
3:构造牛顿方向:
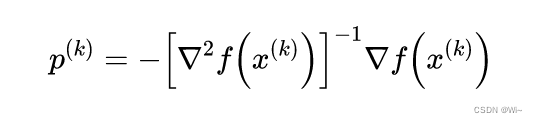
4:算法迭代：
计算 x ( k + 1 ) = x ( k ) + p ( k ) x^{(k+1)} = x^{(k)} + p^{(k)} x(k+1)=x(k)+p(k)，以 x ( k + 1 ) x^{(k+1)} x(k+1)作为下一轮迭代点，令 k : = k + 1 k := k+1 k:=k+1,转第2步。
4：举例
试用牛顿法求函数
f
(
x
)
=
x
1
2
+
25
x
2
2
f(x) = x_1^2 + 25x_2^2
f(x)=x12+25x22 的极小点,其中初始点为
x
(
0
)
=
(
2
,
2
)
T
x^{(0)} = (2, 2)^T
x(0)=(2,2)T,
ε
=
1
0
−
6
ε = 10^{-6}
ε=10−6.
解(1)求梯度和黑塞矩阵：
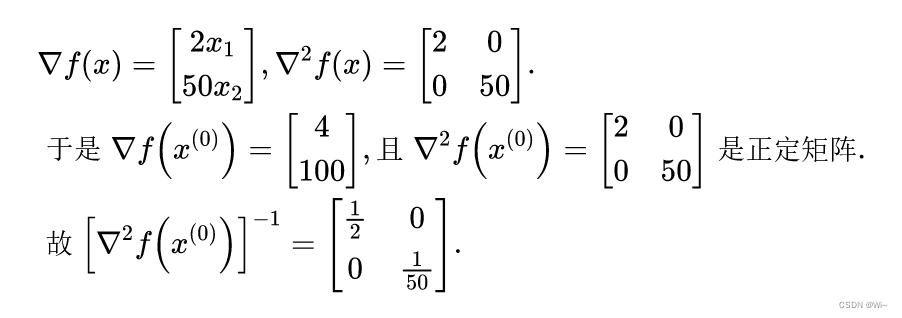
(2)确定牛顿方向：
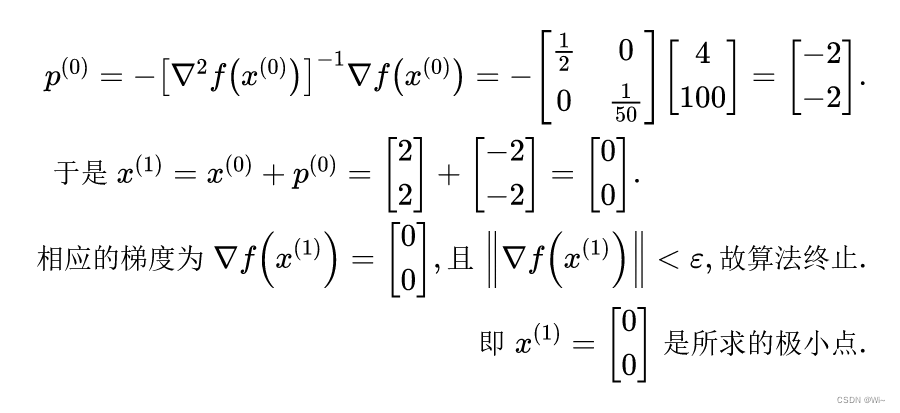即：
x
1
=
0
，
x
2
=
0
x_1 = 0，x_2=0
x1=0，x2=0
这里使用三维坐标系来查看
x
1
=
0
，
x
2
=
0
x_1 = 0，x_2=0
x1=0，x2=0存在极值
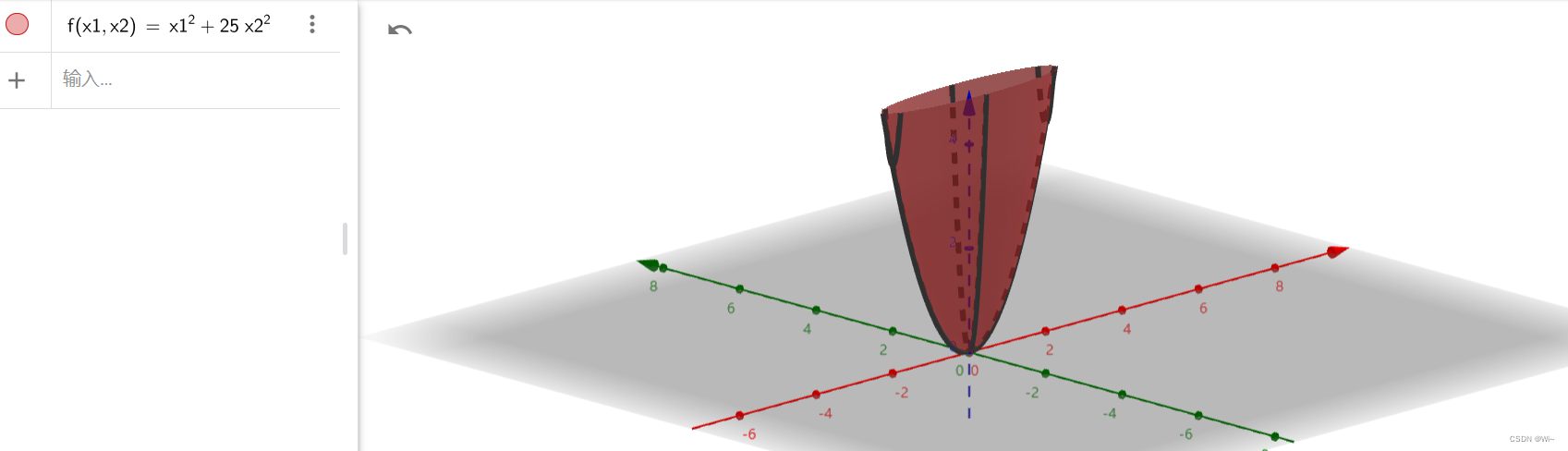
二：高斯牛顿法 （Gauss–Newton algorithm）
1：概述
高斯-牛顿算法用于求解非线性最小二乘问题，相当于最小化函数值的平方和。它是牛顿求非线性函数最小值方法的扩展。由于平方和必须是非负的，因此该算法可以看作是使用牛顿法迭代地逼近和的零点，从而使和最小化。它的优点是不需要计算可能具有挑战性的二阶导数（也就是黑塞矩阵）。
这里说一下，牛顿法使用黑塞矩阵有个缺点：计算量特别大。高斯牛顿法是在牛顿法的基础上用雅可比矩阵代替了黑森矩阵。
注意：高斯牛顿法针对非线性最小二乘问题。最小二乘详解
2：高斯牛顿法推导
①：目标函数问题：自变量
x
x
x 经过模型函数得出因变量
y
y
y，
m
m
m个观测点：
X
=
[
x
1
,
x
2
,
.
.
.
x
m
]
T
X=[x_1,x_2,...x_m]^T
X=[x1,x2,...xm]T，
Y
=
[
y
1
,
y
2
,
.
.
.
y
m
]
T
Y=[y_1,y_2,...y_m]^T
Y=[y1,y2,...ym]T
②：模型函数：
Y
=
f
(
X
;
β
1
,
β
2
,
.
.
.
,
β
n
)
Y = f(X;β_1,β_2,...,β_n)
Y=f(X;β1,β2,...,βn) =>
f
(
x
;
β
)
f(x;β)
f(x;β)
其中 x x x 是自变量 ， y y y 是因变量， β β β 是目标参数。 x 和 y x和y x和y是已知的，优化 β β β 目标参数。
③：优化目标函数：
m
i
n
S
=
∑
i
=
1
n
(
f
(
x
i
;
β
)
−
y
i
)
2
min S = \displaystyle\sum_{i=1}^{n}(f(x_i;β)-y_i)^2
minS=i=1∑n(f(xi;β)−yi)2
④：第
i
i
i 次观测点的预测偏差：
r
i
=
f
(
x
i
;
β
)
−
y
i
)
2
r_i = f(x_i;β)-y_i)^2
ri=f(xi;β)−yi)2，那么每次的偏差组成一个向量形式：
R
=
[
r
1
,
r
2
,
.
.
.
r
m
]
T
R = [r_1,r_2,...r_m]^T
R=[r1,r2,...rm]T
⑤：对于③目标函数 可以写成：
m
i
n
S
=
∑
i
=
1
n
r
i
2
=
R
T
R
min S = \displaystyle\sum_{i=1}^{n}r_i^2 = R^TR
minS=i=1∑nri2=RTR
⑥：那么目标函数梯度：
▽
S
(
β
)
=
[
∂
S
∂
β
1
,
∂
S
∂
β
2
,
.
.
.
,
∂
S
∂
β
n
]
T
▽S(β) = [\frac{\partial S}{\partial β_1},\frac{\partial S}{\partial β_2},...,\frac{\partial S}{\partial β_n}]^T
▽S(β)=[∂β1∂S,∂β2∂S,...,∂βn∂S]T，其中对每个参数
β
j
β_j
βj 求偏导
∂
S
∂
β
j
=
2
∑
i
=
1
m
r
i
∂
r
i
∂
β
j
\frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j}
∂βj∂S=2i=1∑mri∂βj∂ri
⑦：对于 R = [ r 1 , r 2 , . . . r m ] T 和 β R = [r_1,r_2,...r_m]^T和β R=[r1,r2,...rm]T和β的偏导形式就可以写成 雅可比矩阵
J ( R ( β ) ) = [ ∂ r 1 ∂ β 1 . . . ∂ r 1 ∂ β n ⋮ ⋱ ⋮ ∂ r m ∂ β 1 . . . ∂ r m ∂ β n ] J(R(β)) = \begin{bmatrix} \frac{\partial r_1}{\partial β_1}&...&\frac{\partial r_1}{\partial β_n}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_m}{\partial β_1}&...&\frac{\partial r_m}{\partial β_n}\end{bmatrix} J(R(β))=⎣⎢⎡∂β1∂r1⋮∂β1∂rm...⋱...∂βn∂r1⋮∂βn∂rm⎦⎥⎤
⑧：目标函数梯度（一阶偏导）：
▽
S
(
β
)
=
[
∂
S
∂
β
1
,
∂
S
∂
β
2
,
.
.
.
,
∂
S
∂
β
n
]
T
=
>
∂
S
∂
β
j
=
2
∑
i
=
1
m
r
i
∂
r
i
∂
β
j
=
>
▽
S
=
2
J
T
R
▽S(β) = [\frac{\partial S}{\partial β_1},\frac{\partial S}{\partial β_2},...,\frac{\partial S}{\partial β_n}]^T => \frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j} => ▽S = 2J^TR
▽S(β)=[∂β1∂S,∂β2∂S,...,∂βn∂S]T=>∂βj∂S=2i=1∑mri∂βj∂ri=>▽S=2JTR
⑨：求目标函数黑塞矩阵（二阶偏导）：
由梯度向量元素
∂
S
∂
β
j
=
2
∑
i
=
1
m
r
i
∂
r
i
∂
β
j
\frac{\partial S}{\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j}
∂βj∂S=2i=1∑mri∂βj∂ri 到黑塞矩阵元素
∂
2
S
∂
β
k
∂
β
j
=
2
∂
∂
β
k
(
∑
i
=
1
m
r
i
∂
r
i
∂
β
j
)
\frac{\partial ^2S}{\partial β_k\partial β_j} = 2\frac{\partial }{\partial β_k} (\displaystyle\sum_{i=1}^{m}r_i\frac{\partial r_i}{\partial β_j})
∂βk∂βj∂2S=2∂βk∂(i=1∑mri∂βj∂ri)，
应用链式法则得：
∂
2
S
∂
β
k
∂
β
j
=
2
∑
i
=
1
m
(
∂
r
i
∂
β
k
∂
r
i
∂
β
j
+
r
i
∂
2
r
i
∂
β
k
∂
β
j
)
\frac{\partial ^2S}{\partial β_k\partial β_j} = 2 \displaystyle\sum_{i=1}^{m}(\frac{\partial r_i}{\partial β_k}\frac{\partial r_i}{\partial β_j} + r_i\frac{\partial^2 r_i}{\partial β_k\partial β_j})
∂βk∂βj∂2S=2i=1∑m(∂βk∂ri∂βj∂ri+ri∂βk∂βj∂2ri)，
其中
O
O
O矩阵元素 ：
O
k
j
=
∑
i
=
1
m
r
i
∂
2
r
i
∂
β
k
∂
β
j
O_{kj} = \displaystyle\sum_{i=1}^{m}r_i\frac{\partial^2 r_i}{\partial β_k\partial β_j}
Okj=i=1∑mri∂βk∂βj∂2ri
黑塞矩阵：
H
=
2
(
J
T
J
+
O
)
H = 2(J^TJ + O)
H=2(JTJ+O)
⑩：写成牛顿法形式：如果模型比较好，其中
O
O
O矩阵
r
i
r_i
ri是趋近于0的。这里就把
O
O
O矩阵忽略掉，方便计算。
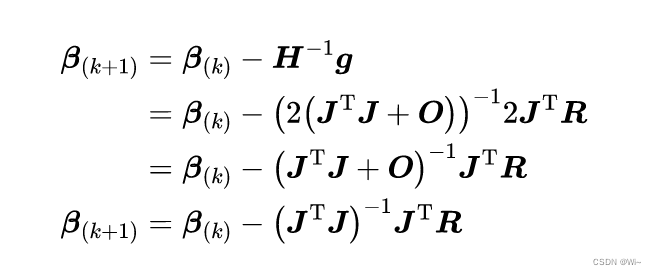
3：高斯牛顿法算法流程
1：给定初始参数值 β 0 β_0 β0 (默认是为 1 1 1 的向量)。设 ε = 1 − 10 ε = 1^{-10} ε=1−10
2：对于第 k k k 次选代，求出当前的雅可比矩阵 J ( β k ) J(β_k) J(βk) 和残差值 f ( β k ) f(β_k) f(βk)也就是 R R R。
3：求解增量方程: H Δ β k = − g H\Delta β_k = -g HΔβk=−g
=> Δ β k = − H − 1 g \Delta β_k= -H^{-1}g Δβk=−H−1g
=> Δ β k ≈ − ( J T J ) − 1 J T R \Delta β_k≈ -(J^TJ)^{-1}J^TR Δβk≈−(JTJ)−1JTR 。这里用雅可比矩阵 J T J J^TJ JTJ 近似黑塞矩阵 H H H。
4：若 Δ β k < ε \Delta β_k<ε Δβk<ε ，则停止。否则，令 β k + 1 = β k + Δ β k β_{k+1} = β_k +\Delta β_k βk+1=βk+Δβk，返回第2步。
4：高斯牛顿法 C++ 代码
//求雅克比矩阵
template <class FunctionPredictedValue>
MatrixXd Jacobi(const VectorXd& inVectorValue, const VectorXd& params,FunctionPredictedValue funPV)
{
int rowNum = inVectorValue.rows();
int colNum = params.rows();
MatrixXd Jac(rowNum, colNum);
for (int i = 0; i < rowNum; i++)
{
for (int j = 0; j < colNum; j++)
{
Jac(i, j) = Deriv(inVectorValue, i, params, j,funPV);
}
}
return Jac;
}
//残差值向量
template <class FunctionPredictedValue>
ArrayXd ResidualsVector(const VectorXd& inVectorValue, const VectorXd& outVectorValue,const VectorXd& params,FunctionPredictedValue funPV)
{
int dataCount = inVectorValue.rows();
//保存残差值
ArrayXd residual(dataCount);
//获取预测偏差值 r= ^y(预测值) - y(实际值)
for(int i=0;i<dataCount;++i)
{
//获取预测值
double predictedValue = funPV(inVectorValue(i),params);
residual(i) = predictedValue - outVectorValue(i);
}
return residual;
}
//求导
template <class FunctionPredictedValue>
double Deriv(const VectorXd& inVectorValue, int objIndex, const VectorXd& params,int paraIndex,FunctionPredictedValue funPV)
{
VectorXd para1 = params;
VectorXd para2 = params;
para1(paraIndex) -= DERIV_STEP;
para2(paraIndex) += DERIV_STEP;
double obj1 = funPV(inVectorValue(objIndex), para1);
double obj2 = funPV(inVectorValue(objIndex), para2);
return (obj2 - obj1) / (2 * DERIV_STEP);
}
/* 高斯牛顿法(GNA) 解决非线性最小二乘问题 确定目标函数和约束来对现有的参数优化
*/
template <class FunctionPredictedValue>
ArrayXd GaussNewtonAlgorithm(const ArrayXd & inVectorValue,const ArrayXd & outVectorValue,ArrayXd params,FunctionPredictedValue funPV,int maxIteCount = 1,double epsilon = 1e-10)
{
int k=0;
//数据个数
int dataCount = inVectorValue.size();
// ε 终止条件
//double epsilon = 1e-10;
//残差值
ArrayXd residual(dataCount);
//found 为true 结束循环
bool found = false;
while(!found && k<maxIteCount)
{
//迭代增加
k++;
//获取预测偏差值 r= ^y(预测值) - y(实际值)
residual = ResidualsVector( inVectorValue, outVectorValue,params, funPV);
//求雅克比矩阵
MatrixXd Jac = Jacobi(inVectorValue,params,funPV);
// Δx = - (Jac^T * Jac)^-1 * Jac^T * r
ArrayXd delta_x = - (((Jac .transpose() * Jac ).inverse()) * Jac.transpose() * residual.matrix()).array();
qDebug()<<QString("高斯牛顿法：第 %1 次迭代 --- 精度：%2 ").arg(k).arg(delta_x.abs().sum());
//达到精度,结束
if(delta_x.abs().sum() < epsilon)
{
found = true;
}
//x(k+1) = x(k) + Δx
params = params + delta_x;
}
return params;
}
Matrix是Eigen库中的一个矩阵类，这里引入Eigen库方便代数运算。
三：列文伯格-马夸尔特法（Levenberg-Marquardt algorithm）
1：概述
在数学和计算中，Levenberg–Marquardt 算法（LMA或简称LM），也称为 阻尼最小二乘法( DLS )，用于解决非线性最小二乘法问题。这些最小化问题尤其出现在最小二乘 曲线拟合中。LMA 在高斯-牛顿算法(GNA) 和梯度下降法之间进行插值。LMA 更稳健比 GNA，这意味着在许多情况下，即使它开始时离最终最小值很远，它也能找到解决方案。对于性能良好的函数和合理的启动参数，LMA 往往比 GNA 慢。LMA 也可以被视为使用信赖域方法的高斯-牛顿。
LMA 在许多软件应用程序中用于解决一般曲线拟合问题。通过使用高斯-牛顿算法，它通常比一阶方法收敛得更快。然而，与其他迭代优化算法一样，LMA 只能找到局部最小值，不一定是全局最小值。与其他数值最小化算法一样，Levenberg–Marquardt 算法是一个迭代过程。要开始最小化，用户必须提供参数向量的初始猜测
β
β
β， 在只有一个最小值的情况下，一个不知情的标准猜测就像
β
=
[
1
,
1
,
.
.
.
,
1
]
T
β = [1,1,...,1]^T
β=[1,1,...,1]T会工作得很好；在有多个最小值的情况下，只有当初始猜测已经有点接近最终解决方案时，算法才会收敛到全局最小值。
2：LM算法流程
1：给定初始参数值 β 0 β_0 β0 (默认是为 1 1 1 的向量)。初始 μ 0 μ_0 μ0的选择可以依赖于 H 0 = J ( β 0 ) T J ( β 0 ) H_0=J(β_0)^TJ(β_0) H0=J(β0)TJ(β0) 中的元素，一般我们选择 μ 0 = τ ∗ m a x i { H i i ( 0 ) } μ_0 =τ*max_i\{H_{ii}^{(0)}\} μ0=τ∗maxi{Hii(0)}，一般 τ = 1 0 − 6 τ=10^{−6} τ=10−6，这里设置 ε 1 = 1 − 10 ε_1 = 1^{-10} ε1=1−10和 ε 2 = 1 − 10 ε_2 = 1^{-10} ε2=1−10。
2：若 ∣ ∣ g ∣ ∣ ∞ ≤ ε 1 ||g||_\infty≤ε_1 ∣∣g∣∣∞≤ε1 成立，则停止。
3：对于第 k k k 次选代，求出当前的雅可比矩阵 J ( β k ) J(β_k) J(βk) 和残差值 f ( β k ) f(β_k) f(βk)也就是 R R R。
4：求解增量方程: ( H + μ k I ) Δ β k = − g (H+μ_kI)\Delta β_k = -g (H+μkI)Δβk=−g
=> Δ β k = − ( H + μ k I ) − 1 g \Delta β_k= -(H+μ_kI)^{-1}g Δβk=−(H+μkI)−1g
=> Δ β k ≈ − ( J T J + μ k I ) − 1 J T R \Delta β_k≈ -(J^TJ+μ_kI)^{-1}J^TR Δβk≈−(JTJ+μkI)−1JTR 。这里用雅可比矩阵 J T J J^TJ JTJ 近似黑塞矩阵 H H H。
5：若 ∣ ∣ Δ β k ∣ ∣ ≤ ε 2 ( ∣ ∣ β k ∣ ∣ + ε 2 ) ||\Delta β_k||≤ε_2(||β_k|| + ε_2) ∣∣Δβk∣∣≤ε2(∣∣βk∣∣+ε2) 成立，则停止。否则，令 β k + 1 = β k + Δ β k β_{k+1} = β_k +\Delta β_k βk+1=βk+Δβk。
6： ρ = ∣ ∣ F ( β k ) ∣ ∣ 2 2 − ∣ ∣ F ( β k + Δ β k ) ∣ ∣ 2 2 L ( 0 ) − L ( Δ β k ) \rho = \frac{||F(β_k)||_2^2-||F(β_k+\Delta β_k)||_2^2}{L(0) - L(\Delta β_k)} ρ=L(0)−L(Δβk)∣∣F(βk)∣∣22−∣∣F(βk+Δβk)∣∣22，如果 ρ > 0 \rho >0 ρ>0，求出当前的黑塞矩阵 H ≈ J ( β k ) T J ( β k ) H ≈ J(β_k)^TJ(β_k) H≈J(βk)TJ(βk) 和梯度 g = J ( β k ) T f ( β k ) g = J(β_k)^Tf(β_k) g=J(βk)Tf(βk)。若 ∣ ∣ g ∣ ∣ ∞ ≤ ε 1 ||g||_\infty≤ε_1 ∣∣g∣∣∞≤ε1 成立，则停止。更新 μ k μ_k μk， μ k = μ k ∗ m a x { 1 3 , 1 − ( 2 ρ − 1 ) 3 } ; v = 2 μ_k =μ_k*max\{\frac{1}{3},1-(2\rho-1)^3\};v=2 μk=μk∗max{31,1−(2ρ−1)3};v=2。如果 ρ ≤ 0 \rho ≤0 ρ≤0， μ k = μ k ∗ v ; v = 2 ∗ v μ_k =μ_k*v; v=2*v μk=μk∗v;v=2∗v。
最终伪代码如下：
3：列文伯格-马夸尔特法 C++ 代码
/* 列文伯格马夸尔特法(LMA) == 使用信赖域的高斯牛顿法，鲁棒性更好， 确定目标函数和约束来对现有的参数优化
*/
template <class FunctionPredictedValue>
ArrayXd LevenbergMarquardtAlgorithm(const ArrayXd &inVectorValue,const ArrayXd & outVectorValue, ArrayXd params,FunctionPredictedValue funPV,int maxIteCount = 1,double epsilon = 1e-10)
{
//数据个数
int dataCount = inVectorValue.size();
// ε 终止条件
//double epsilon = 1e-10;
// τ
double tau = 1e-6;
//迭代次数
int k=0;
int v=2;
//求雅可比矩阵
MatrixXd Jac = Jacobi(inVectorValue,params,funPV);
//用雅可比矩阵近似黑森矩阵
MatrixXd Hessen = Jac .transpose() * Jac ;
//获取预测偏差值 r= ^y(预测值) - y(实际值)
//保存残差值
ArrayXd residual = ResidualsVector(inVectorValue, outVectorValue,params,funPV);
//梯度
MatrixXd g = Jac.transpose() * residual.matrix();
//found 为true 结束循环
bool found = ( g.lpNorm<Eigen::Infinity>() <= epsilon );
//阻尼参数μ
double mu = tau * Hessen.diagonal().maxCoeff();
while(!found && k<maxIteCount)
{
k++;
//LM方向 uI => I 用黑森矩阵对角线代替
//MatrixXd delta_x = - (Hessen + mu*Hessen.asDiagonal().diagonal()).inverse() * g;
MatrixXd delta_x = - (Hessen + mu*MatrixXd::Identity(Hessen.cols(), Hessen.cols())).inverse() * g;
if( delta_x.lpNorm<2>() <= epsilon * (params.matrix().lpNorm<2>() + epsilon ))
{
qDebug()<<QString("LM：第 %1 次迭代 --- 精度：%2 ").arg(k).arg(delta_x.lpNorm<2>());
found = true;
}
else
{
MatrixXd newParams = params + delta_x.array();
//保存残差值
ArrayXd residualOld(dataCount),residualNew(dataCount);
//获取预测偏差值 r= ^y(预测值) - y(实际值) 旧值
residualOld = ResidualsVector( inVectorValue, outVectorValue,params, funPV);
//获取预测偏差值 r= ^y(预测值) - y(实际值) 新值
residualNew = ResidualsVector( inVectorValue, outVectorValue,newParams, funPV);
//ρ (-(delta_x.transpose()*g) - 0.5*(delta_x.transpose() * Hessen * delta_x)).sum();
double rho = (residualOld.pow(2).sum() - residualNew.pow(2).sum()) / (0.5*delta_x.transpose()*(mu * delta_x - g)).sum() ;
if(rho>0)
{
params = newParams;
Jac = Jacobi(inVectorValue,params,funPV);
Hessen = Jac.transpose() * Jac ;
//获取预测偏差值 r= ^y(预测值) - y(实际值)
residual = ResidualsVector( inVectorValue, outVectorValue,params, funPV);
g = Jac.transpose() * residual.matrix();
found = ( g.lpNorm<Eigen::Infinity>() <= epsilon );
qDebug()<<QString("LM：第 %1 次迭代 --- 精度：%2 ").arg(k).arg(g.lpNorm<Eigen::Infinity>());
mu = mu* qMax(1/3.0 , 1-qPow(2*rho -1,3));
v=2;
}
else
{
mu = mu*v;
v = 2*v;
}
}
}
return params;
}
//FunctionPredictedValue 是一个自定义函数，可以定义自己的函数 规则
//设置规则,获取预测值 ==》自变量和参数
//曲线拟合函数
class CurveFittingFunction
{
public:
double operator()(const double &inValue ,const ArrayXd ¶ms)
{
double value=0;
int paramsCount = params.rows();
for(int i=0;i<paramsCount;++i)
{
//这里使用曲线方程 y = a1*x^0 + a2*x^1 + a3*x^2 + ... 根据参数(a1,a2,a3,...)个数来设置
value += params(i) * qPow(inValue,i);
}
return value;
}
};
四：总结
1：工具：主要Qt + Eigen库 + QCustomPlot类
Eigen库是一个用于矩阵计算，代数计算库
QCustomPlot类是一个用于绘图和数据可视化
2：上面完整代码已上传GitHub
3：参考文献
黑塞矩阵和雅可比矩阵理解
高斯牛顿法详解
LM算法详解
LM论文
