Problem - C - Codeforces

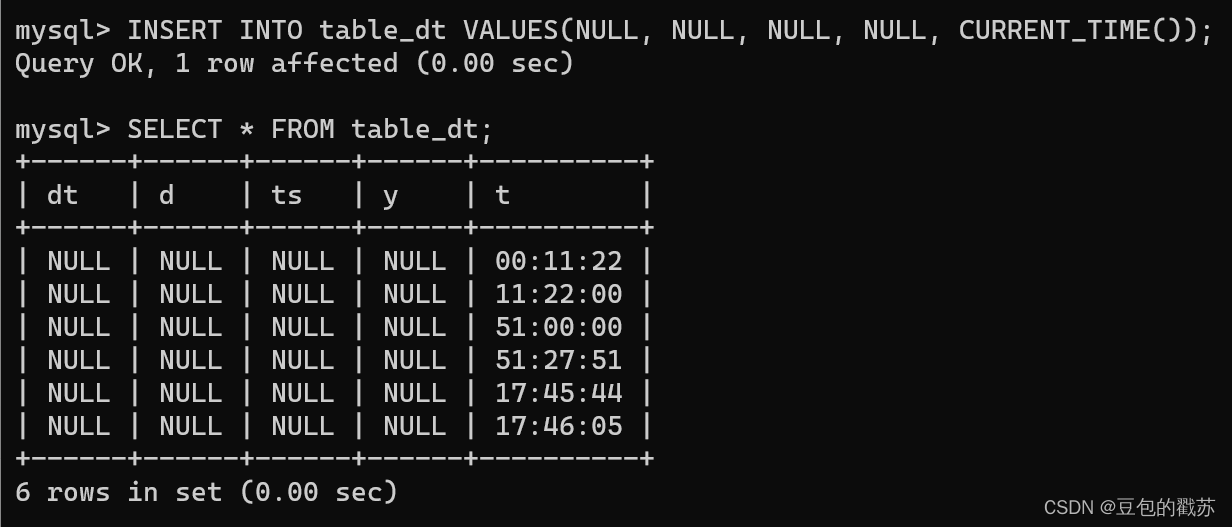
You需要油漆一个由n个部分组成的长围栏。不幸的是,它没有被涂漆,所以你决定雇用q名画家来完成这项工作。第i名画家将会油漆所有满足lisxsri的部分x.
不幸的是,你的预算很紧,所以你只能雇用q-2名画家。显然,只有你雇用的画家才会完成他们的工作。
如果你选择最优的q-2名画家,你希望最大化已经涂漆的部分数量。如果至少有一名画家对一个部分进行了涂漆,则认为该部分已经涂漆。
输入
第一行包含两个整数n和q (3≤n,q≤5000)--分别是部分数和可供聘用的画家数。
接下来有q行,每行描述其中一位画家:第i行包含两个整数li和ri (1<lisri≤n)。
输出
输出—个整数--如果你雇用q-2名画家,最大可以涂漆的部分数量。
Examples
input
Copy
7 5 1 4 4 5 5 6 6 7 3 5
output
Copy
7
input
Copy
4 3 1 1 2 2 3 4
output
Copy
2
input
Copy
4 4 1 1 2 2 2 3 3 4
output
Copy
3
题解:
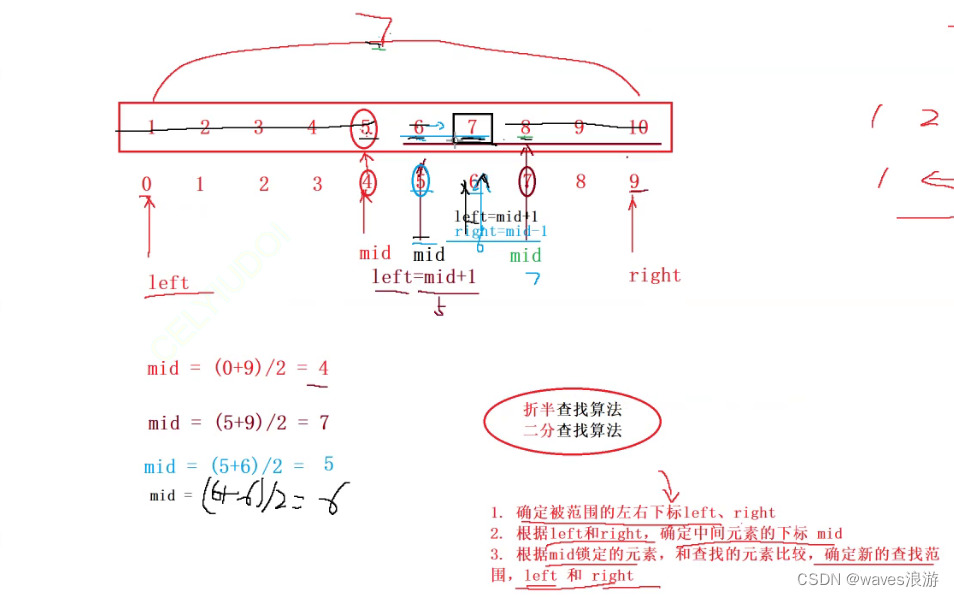
首先我们可以记录如果所有人涂,每个点会涂几次,由于数据比较小,差分都不用,直接暴力即可
关键是,我们如何,减去两个人涂的影响呢?
其中一个人我么可以通过,枚举q个人时,让l[i] ~ r[i]这一段区间都减一,这样消去了一个影响,那另一个人呢?
我们这侯就可以用到前缀和了,通过前缀和记录,1~n当前为止,被染的次数1的数量有多少,并且记录n有多少个点被染过,
接着我么枚举i + 1~n,ans = max(ans,sum - pre[r[j]] - pre[l[j]-1]);
通过前缀和可以快速得到,每一段如果不涂的影响(影响就是被涂次数为一的数量)
本题主要考点为,利用前缀和求任意一段得影响(前缀和应用十分广泛的一种思路,不应该想不到的)
#include <cstdio>
#include <cstring>
#include <algorithm>
#include<iostream>
#include<vector>
#include<set>
#include<map>
#include<cmath>
#include<queue>
using namespace std;
typedef long long ll;
#define int long long
typedef pair<int,int> PII;
int mod = 1e9 + 7;
int l[5005];
int r[5005];
int cnt[5005];
int pre[5005];
void solve()
{
int n,q;
cin >> n >> q;
for(int i = 1;i <= q;i++)
{
cin >> l[i] >> r[i];
for(int j = l[i];j <= r[i];j++)
cnt[j]++;
}
int ans = 0;
for(int i = 1;i <= q;i++)
{
for(int j = l[i];j <= r[i];j++)
cnt[j]--;
int sum = 0;
for(int j = 1;j <= n;j++)
{
if(cnt[j] == 1)
pre[j] = pre[j - 1] + 1;
else
pre[j] = pre[j - 1];
if(cnt[j])
sum++;
}
for(int j = i + 1;j <= q;j++)
{
ans = max(ans,sum - (pre[r[j]] - pre[l[j] - 1]));
}
for(int j = l[i];j <= r[i];j++)
cnt[j]++;
}
cout << ans;
}
//5 7 8 9 10
signed main()
{
// ios::sync_with_stdio(0);
// cin.tie(0);cout.tie(0);
int t = 1;
// cin >> t;
while(t--)
{
solve();
}
}