1、Mortal Fibonacci Rabbits
- Problem
- Sample Dataset
- Sample Output
- Code
- Output
2、Overlap Graphs
- Problem
- Sample Dataset
- Sample Output
- Code
- Output
3、Calculating Expected Offspring
- Problem
- Sample Dataset
- Sample Output
- Code
- Output
4、Finding a Shared Motif
- Problem
- Sample Dataset
- Sample Output
- Code
- Output
5、Independent Alleles
- Problem
- Sample Dataset
- Sample Output
- example
- Code
- Output

1、Mortal Fibonacci Rabbits

Problem

回想一下Part 1“Rabbits and Recurrence Relations”中的斐波那契数的定义，它遵循循环关系F(n)=F(n-1)+F(n-2)。每对兔子在一个月内达到成熟，并在随后的每个月产生一对后代（一公一母）。现在假设所有兔子在m月后死亡，如图所示，当m=3时，意味着一对兔子在死亡之前只繁殖两次。

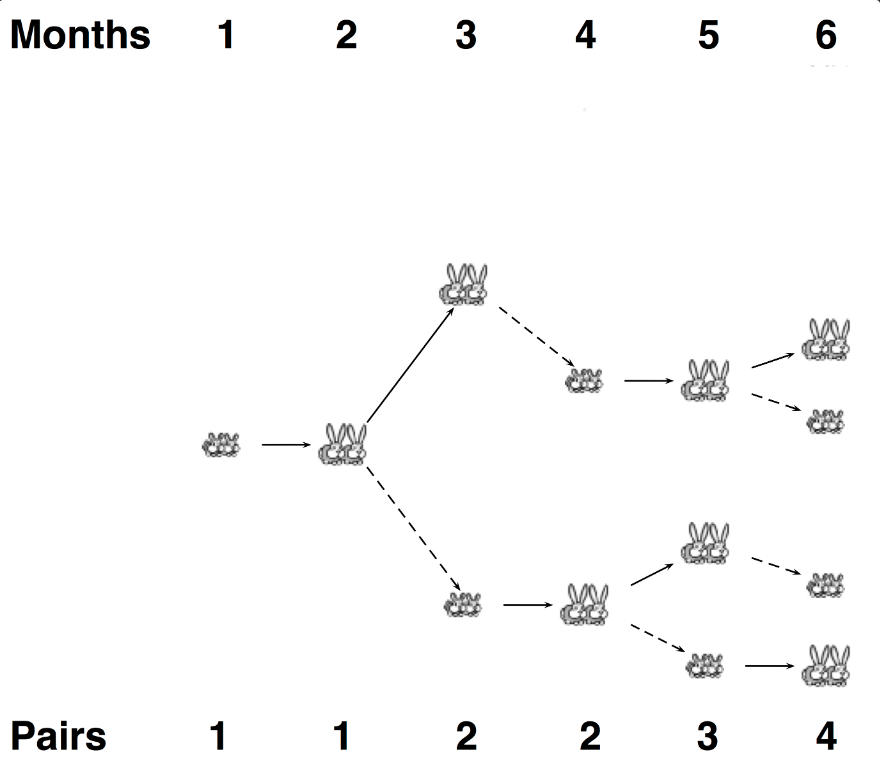
A figure illustrating the propagation of Fibonacci's rabbits if they die after three months.

Given： n，m为正整数，n≤100，m≤20

Return： 如果所有兔子都活了m个月，那么第n个月后剩下的兔子总数

Sample Dataset

6 3

Sample Output

Code

# Mortal Fibonacci Rabbits

def rabbits_number(n, m):
    # 前两个月兔子均为1对
    # python索引从0开始，列表第一个设置为0是为了让索引从1开始
    number_list = [0, 1, 1]
    for i in range(3, n+1):
        # m+1月之前，F(n)=F(n-1)+F(n-2)
        if i < m+1:
            number_list.append(number_list[i - 1] + number_list[i - 2])
        # m+1月时，F(n)=F(n-1)+F(n-2)-1
        elif i == m+1:
            number_list.append(number_list[i - 1] + number_list[i - 2] - 1)
        # m+1月之后，F(n)=F(n-1)+F(n-2)-F(n-m-1)
        elif i > m+1:
            number_list.append(number_list[i - 1] + number_list[i - 2] - number_list[i - m - 1])
    return number_list[n]


print(rabbits_number(6, 3))

with open("rosalind_fibd.txt", "r") as f:
    text = f.read().split()
    n = int(text[0])
    m = int(text[1])
    print(rabbits_number(n, m))

Output

4
2870048561233731259

2、Overlap Graphs

Problem

重叠图（overlap graph）是一个有向图（directed graph），其中集合中的每个字符串都由一个节点表示，如果s的某个后缀等于t的前缀，则节点s通过有向边连接到t。

Given： FASTA格式的DNA字符串集合，其总长度最多为10kbp

Return： The adjacency list corresponding to O3（计算一条序列最后3个碱基的与另一条序列的前面3个碱基是否相同，如果相同就将两条序列名称输出）

Sample Dataset

>Rosalind_0498
AAATAAA
>Rosalind_2391
AAATTTT
>Rosalind_2323
TTTTCCC
>Rosalind_0442
AAATCCC
>Rosalind_5013
GGGTGGG

Sample Output

Rosalind_0498 Rosalind_2391
Rosalind_0498 Rosalind_0442
Rosalind_2391 Rosalind_2323

Code

# Overlap Graphs

def read_fasta(file):
    sequences = {}
    with open(file, "r") as f:
        for line in f:
            line = line.strip()
            if line[0] == ">":
                name = line[1:]
                sequences[name] = ""
            else:
                sequences[name] += line
    return sequences


def overlap_graph(dictionary, k=3):
    edges = []
    for name1 in dictionary:
        for name2 in dictionary:
            if name1 != name2 and dictionary[name1][-k:] == dictionary[name2][:k]:
                edges.append((name1, name2))
    return edges


dna_strings = read_fasta("code2_example.txt")
edges = overlap_graph(dna_strings)
for edge in edges:
    print(edge[0], edge[1])

print("------")

dna_strings = read_fasta("rosalind_grph.txt")
edges = overlap_graph(dna_strings)
for edge in edges:
    print(edge[0], edge[1])

Output

Rosalind_0498 Rosalind_2391
Rosalind_0498 Rosalind_0442
Rosalind_2391 Rosalind_2323
------
Rosalind_3127 Rosalind_7657
..........（省略）..........
Rosalind_3675 Rosalind_1200

3、Calculating Expected Offspring

Problem

在概率论和统计学中，一个离散性随机变量的期望值（或数学期望，亦简称期望，物理学中称为期待值）是试验中每次可能的结果乘以其结果概率的总和。换句话说，期望值像是随机试验在同样的机会下重复多次，所有那些可能状态平均的结果，便基本上等同“期望值”所期望的数。

例如，掷一枚公平的六面骰子，其每次“点数”的期望值是3.5，计算如下：

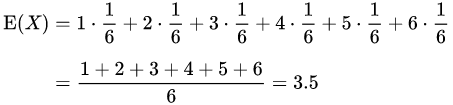
不过如上所说明的，3.5虽是“点数”的期望值，但却不属于可能结果中的任一个，没有可能掷出此点数。

Given： 六个非负整数，每个都不超过20000。按照顺序，六个给定的整数代表具有以下基因型的夫妇的数量：1.AA-AA 2.AA-Aa 3.AA-aa 4.Aa-Aa 5.Aa-aa 6.aa-aa

Return： 在假定每对夫妇正好有两个后代的情况下，在下一代中拥有显性表型的后代的期望数目。

Sample Dataset

1 0 0 1 0 1

Sample Output

3.5

Code

# Calculating Expected Offspring

def expected_offspring(str):
    lists = [int(i) for i in str.strip().split(" ")]
    # 每个基因型的夫妇生育带有显性基因孩子的概率
    prob = [1, 1, 1, 0.75, 0.5, 0]
    expected = 0
    for i in range(len(lists)):
        expected += lists[i] * prob[i]
    # 两个孩子
    expected = expected * 2
    return expected


example = "1 0 0 1 0 1"
print(expected_offspring(example))

with open("rosalind_iev.txt", "r") as f:
    given = f.read()
    print(expected_offspring(given))

Output

3.5
165791.0

4、Finding a Shared Motif

Problem

字符串集合的公共子字符串是集合中所有字符串的子字符串。例如，“CG”是“ACGTACGT”和“AACCGTATA”的公共子串，但它不是最长的公共子串；“CGTA”才是“ACGTACGT”和“AACCGTATA”最长的公共子串。注意，最长公共子串不一定是唯一的；举个简单的例子，“AA”和“CC”都是“AACC”和“CCAA”的最长公共子串。

Given： k（k≤100）个长度不超过1 kbp的FASTA格式的DNA串的集合。

Return： 集合中最长的公共子字符串。（如果存在多个，可以返回任意一个）

Sample Dataset

>Rosalind_1
GATTACA
>Rosalind_2
TAGACCA
>Rosalind_3
ATACA

Sample Output

AC

Code

# Finding a Shared Motif

def read_fasta(file):
    sequences = {}
    with open(file, "r") as f:
        for line in f.readlines():
            line = line.strip()
            if line[0] == ">":
                name = line[1:]
                sequences[name] = ""
            else:
                sequences[name] += line
    return sequences


def find_shared_motif(sequences):
    # 寻找最短的序列
    min_len = 100000
    shortest_seq = ""
    for seq in sequences.values():
        if len(seq) < min_len:
            min_len = len(seq)
            shortest_seq = seq
    # print(shortest_seq)

    # 将最短的序列所有非重复的子字符串存储到集合中
    # 集合中，重复的元素只保留一个
    shared_motif = set()
    for i in range(len(shortest_seq)):
        for j in range(i + 1, len(shortest_seq) + 1):
            shared_motif.add(shortest_seq[i:j])
    # print(shared_motif)

    # 将最短序列的子字符串分别与其余序列比较
    # 剔除集合中与其余序列没有重合的子字符串
    for seq in sequences.values():
        new_shared_motif = list(shared_motif)
        for fragment in new_shared_motif:
            if fragment not in seq:
                shared_motif.remove(fragment)
    # print(shared_motif)

    # 随机输出一个最长的公共子字符串
    max_len = 0
    longest_motif = ""
    for fragment in shared_motif:
        if len(fragment) >= max_len:
            max_len = len(fragment)
            longest_motif = fragment

    return longest_motif


example = read_fasta("code4_example.txt")
print(find_shared_motif(example))

seqs = read_fasta("rosalind_lcsm.txt")
print(find_shared_motif(seqs))

Output

CA
TAGGCTCCCTGTGGCTCCCATCAATGTGCCTCGTAATACT

5、Independent Alleles

Problem

自由组合定律和独立分配律（孟德尔第二定律）

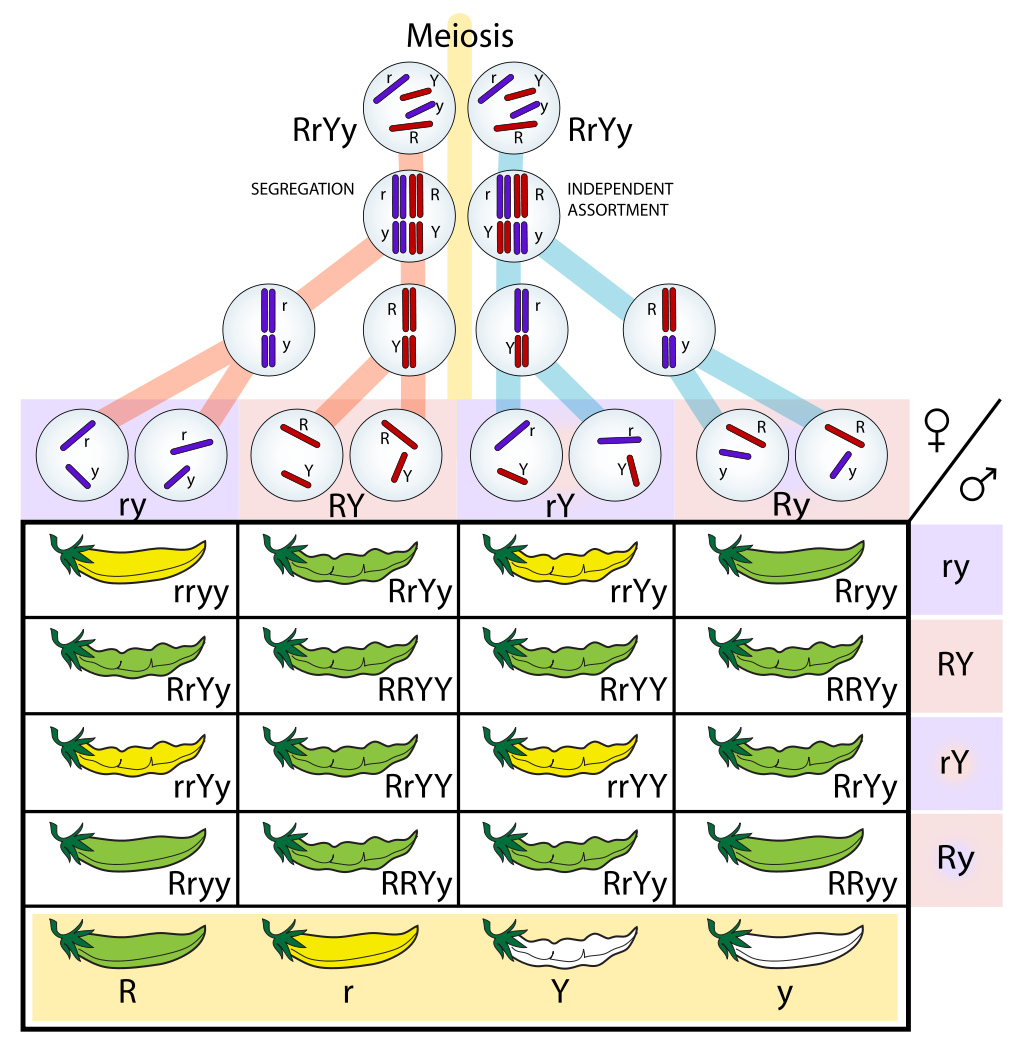
从孟德尔的碗豆杂交实验可以得出以下结论： ①亲代父本与母本体内各有一成对因子（基因）可决定遗传特征。 ②此一成对因子在杂交的过程中会分开，重新进行组合。（第一定律） ③不同遗传特征的基因独立而不互相干扰。（第二定律）

Given： $k，N为正整数，k≤7，N≤2^k$ 亲代基因型为AaBb，有两个子一代，每个子一代又各产生两个子二代，以此类推，每代都与基因型为AaBb的个体交配。

Return： 在满足自由组合定律的前提下，第k代有至少N个AaBb基因型个体的概率。

Sample Dataset

2 1

Sample Output

0.684

example

当k=2，N=1时

亲代：AaBb × AaBb
子代基因型为AaBb的概率：
P(AaBb)=P(Aa)×P(Bb)=0.5×0.5=0.25

以x表达在n次试验中事件A出现的次数。x是一个离散型随机变量，例如0，1，2，…，n，其概率分布函数为
$C^x_nP^xq^{n-x}$
其中，
$C^x_n = \frac{n!}{x!(n-x)!}$
我们称P(x)为随机变量x的二项分布，记作B(n,p)

所以，第2代一共有4个孩子，至少有1个AaBb基因型的概率为:
$P = P (1) + P (2) + P (3) + P (4) = 0.684$
其中：
$\begin{align*} P(1)&=C^1_4p^1(1-p)^3\\ &=4×0.25×0.75^3=0.4219 \end{align*}$
$\begin{align*} P(2)&=C^2_4p^2(1-p)^2\\ &=6×0.25^2×0.75^2=0.2109 \end{align*}$
$\begin{align*} P(3)&=C^3_4p^3(1-p)^1\\ &=4×0.25^3×0.75=0.0469 \end{align*}$
$\begin{align*} P(4)&=C^4_4p^4(1-p)^0\\ &=1×0.25^4×0.75^0=0.0039 \end{align*}$

Code

# Independent Alleles


def factorial(n):
    """阶乘"""
    f = 1
    for i in range(1, n + 1):
        f = f * i
    return f


def combination(i, j):
    """二项式系数"""
    return factorial(i) / (factorial(j) * factorial(i - j))


def independent_alleles(k, n):
    p = 0
    # count 为第k代人数
    # pow(x,y) x的y次方的值
    count = pow(2, k)
    for i in range(n, count + 1):
        p += combination(count, i) * pow(0.25, i) * pow(0.75, count - i)
    return p


p = independent_alleles(2, 1)
print('%.3f' % p)

with open("rosalind_lia.txt", "r") as f:
    text = f.read().strip().split()
    k = int(text[0])
    n = int(text[1])
    p = independent_alleles(k, n)
    print('%.3f' % p)