我们还是用例子来引入本次要探讨的问题--尾调用
#include <stdio.h>
int fib(int a)
{
return a <= 2 ? 1 : fib(a - 1) + fib(a - 2);
}
int main()
{
int n,result;
scanf("%d",&n);
result = fib(n);
printf("result is %d.\n",result);
return 0;
}这段代码的含义应该很清晰。那下面这一段呢?
#include <stdio.h>
int repeat = 0;
int fib(int a)
{
int result;
if (a <= 2) return 1;
if ((a - 1) <= 2) { // a <= 3 的情况
result = 1;
} else {
result = fib(a - 2) + fib(a - 3);
}
if ((a - 2) <= 2) { // a <= 4 的情况
result += 1;
} else {
result += fib(a - 3) + fib(a - 4);
}
return result;
}
int main()
{
int n;
int result;
scanf("%d",&n);
result = fib(n);
printf("result is %d.\n",result);
return 0;
}这两个代码在功能上是一致的,只不过第二个代码把a <= 3 和 a <= 4 的情况也单独拎出来,类似于之前提到的循环展开(Compiler- 循环展开_青衫客36的博客-CSDN博客),也是为了提高效率
我们对上面的两个程序稍作修改,加上计时函数,如下所示
// fib.c
#include <stdio.h>
#include <time.h>
clock_t to_duration_in_ms(clock_t start, clock_t end)
{
return 1000 * (end - start) / CLOCKS_PER_SEC;
}
int repeat = 0;
int fib(int a)
{
repeat ++;
return a <= 2 ? 1 : fib(a - 1) + fib(a - 2);
}
int main()
{
int n,result;
clock_t start, end;
scanf("%d",&n);
start = clock();
result = fib(n);
end = clock();
printf("result is %d,time is %ldms,repeat is %d.\n",result,to_duration_in_ms(start,end),repeat);
return 0;
}// fib1.c
#include <stdio.h>
#include <time.h>
clock_t to_duration_in_ms(clock_t start, clock_t end)
{
return 1000 * (end - start) / CLOCKS_PER_SEC;
}
int repeat = 0;
int fib(int a)
{
int result;
repeat ++;
if (a <= 2) return 1;
if ((a - 1) <= 2) {
result = 1;
} else {
result = fib(a - 2) + fib(a - 3);
}
if ((a - 2) <= 2) {
result += 1;
} else {
result += fib(a - 3) + fib(a - 4);
}
return result;
}
int main()
{
int n,result;
clock_t start, end;
scanf("%d",&n);
start = clock();
result = fib(n);
end = clock();
printf("result is %d,time is %ldms,repeat is %d.\n",result,to_duration_in_ms(start,end),repeat);
return 0;
}然后来对比一下这两个程序的运行时间time和重复次数repeat
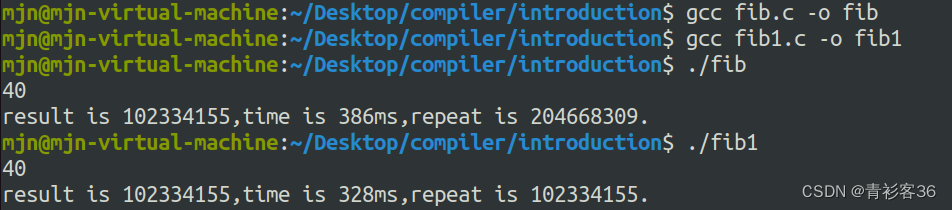
可以看到两个程序的运行结果是一样的,但是运行时间和重复次数明显第二个更优。
为什么会出现这样的差别呢?
我们以fib(3)为例,来看看在这两个代码中是如何执行的。
● 对于第一段代码,fib(3)->fib(2)+fib(1);fib(2)进行递归,返回1;fib(1)进行递归,返回1。
● 对于第二段代码,在两个if条件判断的第一个分支处返回。
所以,第二段代码节省了不少的函数调用的时间。而我们知道,函数调用,要分配栈,要传参总是要花费时间的。
下面我们来看看编译器优化的效果,使用GCC进行编译,选择-O3,查看运行时间。

相比于之前的386ms和328ms,经过O3优化后的132ms还是很厉害的hh~
那如果不用递归,而是用循环的方式计算斐波那契数列呢?我们来看下面代码的执行时间。
// fibc.c
#include <stdio.h>
#include <time.h>
clock_t to_duration_in_ms(clock_t start, clock_t end)
{
return 1000 * (end - start) / CLOCKS_PER_SEC;
}
int repeat = 0;
int fibc(int n)
{
int f1 = 1;
int f2 = 1;
int result;
if(n == 1 || n == 2) return 1;
else {
for(int i = 2; i < n; i++)
{
result = f1 + f2;
f1 = f2;
f2 = result;
}
}
return result;
}
int main()
{
int n;
int result;
clock_t start, end;
scanf("%d",&n);
start = clock();
result = fibc(n);
end = clock();
printf("result is %d,time is %dms,repeat is %d.\n",result,to_duration_in_ms(start,end),repeat);
return 0;
}
运行时间为惊人的0ms,由此可以体会到函数调用、递归执行的效率问题。
我们在学习递归和迭代的时候,也会知道递归的代码容易看懂,而迭代展开的代码不好懂。
那有没有一种方法既是递归,并且效率又比较高呢?(本质上是降低函数调用的代价)
这种方式是尾递归,特点是,这种调用在整个函数的最后一步,它调用完之后整个函数就结束了,由于这是函数最后一步,做完之后函数调用堆栈框架也可以拆除了。注意,此种写法,斐波那契数列的加法操作是在参数传递这个过程中完成的。
因为这个调用发生在函数的最后一部分,所以在优化时,每当进行函数调用,就没必要重新分配栈了,这样就把函数调用的代价降到很低。
#include <stdio.h>
#include <time.h>
clock_t to_duration_in_ms(clock_t start, clock_t end)
{
return 1000 * (end - start) / CLOCKS_PER_SEC;
}
int repeat = 0;
int fibtail(int n,int ret1, int ret2)
{
if(n==1) return ret1;
else return fibtail(n-1,ret2, ret1+ret2);
}
int main()
{
int n;
int result;
clock_t start, end;
scanf("%d",&n);
start = clock();
result = fibtail(n,1,1);
end = clock();
printf("result is %d,time is %dms,repeat is %d.\n",result,to_duration_in_ms(start,end),repeat);
}我们看一下这个程序的运行时间

我们来分析一个简单的尾调用
#include <stdio.h>
int x = 1;
int g(int z)
{
return x + z;
}
int f(int y)
{
int x = y + 1;
return g(y*x);
}
int main(){
printf("The result is %d.\n",f(3));
return 0;
}看一下生成的汇编代码。
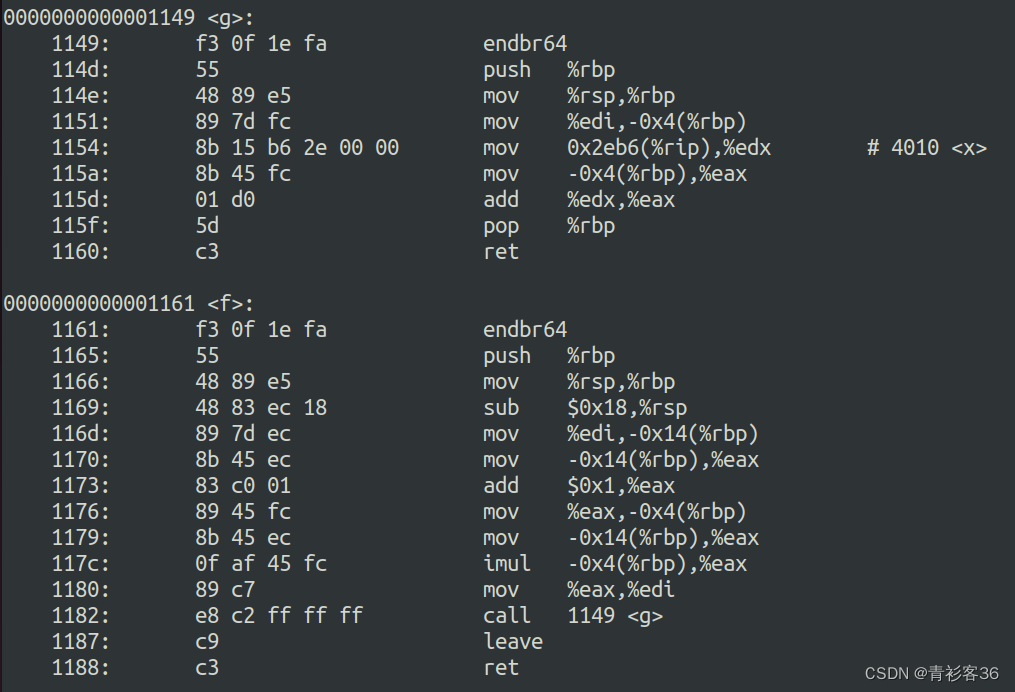
以下是开启-O3优化的情况:
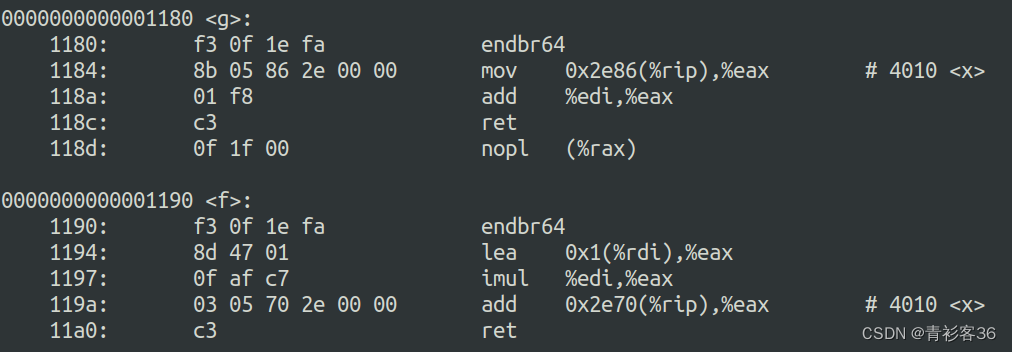
可以看到,在函数f和g中,代码得到了大幅的缩减。甚至,在优化之后,两个函数都没有分配栈空间,直接进行了计算。再进一步的,函数f并没有调用函数g,而是直接把函数g的工作给做了。所以,这种优化真是很了不起的。
以上为中科大软件学院《编译工程》课后总结,感谢郭燕老师的倾心教授,老师讲的太好啦(^_^)