文章目录

1、Leetcode 312.戳气球（困难）
- 1.1 题目描述
- 1.2 思路分析
- 1.3 代码实现
- 1.4 启示
2、Leetcode 546.移除盒子（困难）
- 2.1 题目描述
- 2.2 思路分析
- 2.3 代码实现
3、消除字符
- 3.1 题目描述
- 3.2 思路分析
- 3.3 代码实现

1、Leetcode 312.戳气球（困难）

1.1 题目描述

给定一个数组 arr，代表一排有分数的气球。

每打爆一个气球都能获得分数，假设打爆气球的分数为 $X$ ，获得分数的规则如下:

如果被打爆气球的左边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为 $L$ ；如果被打爆气球的右边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为 R。获得分数为 $L * X * R$ 。
如果被打爆气球的左边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为 $L$ ；如果被打爆气球的右边所有气球都已经被打爆。获得分数为 $L * X$ 。
如果被打爆气球的左边所有的气球都已经被打爆；如果被打爆气球的右边有没被打爆的气球，找到离被打爆气球最近的气球，假设分数为 $R$ 。获得分数为 $X * R$ 。
如果被打爆气球的左边和右边所有的气球都已经被打爆。获得分数为 $X$ 。

目标是打爆所有气球，获得每次打爆的分数。通过选择打爆气球的顺序，可以得到不同的总分，请返回能获得的最大分数。

【举例】

arr = {3,2,5}

如果先打爆3，获得 $3 * 2$ ；再打爆2，获得 $2 * 5$ ；最后打爆5，获得5；最后总分21。
如果先打爆3，获得 $3 * 2$ ；再打爆5，获得 $2 * 5$ ；最后打爆2，获得2；最后总分18。
如果先打爆2，获得 $3 * 2 * 5$ ；再打爆3，获得 $3 * 5$ ；最后打爆5，获得5；最后总分50。
如果先打爆2，获得 $3 * 2 * 5$ ；再打爆5，获得 $3 * 5$ ；最后打爆3，获得3；最后总分48。
如果先打爆5，获得 $2 * 5$ ；再打爆3，获得 $3 * 2$ ；最后打爆2，获得2；最后总分18。
如果先打爆5，获得 $2 * 5$ ；再打爆2，获得 $3 * 2$ ；最后打爆3，获得3；最后总分19。

返回能获得的最大分数为50。

1.2 思路分析

首先，很自然地想在 $L$ 到 $R$ 范围上枚举第一个打爆的气球inf f(arr, L, R)，但是这个局部尝试的方法不行，因为选择打爆的气球左右两边的气球情况是不知道的，但是两边的气球是会决定分数的。所以，一定是要加参数的。

注意，如果设计的函数的返回值只由可变参数决定，如果是，那就是一个无后效性问题，即可变参数一定，返回值就是确定的。而本题不符合，只给定 $L$ 和 $R$ 参数的值，不能决定最后的得分。

接下来说解法：

依然设计函数 int f(int[] arr, int L, int R)，返回值表示得到的最大得分，但是需要满足潜台词：的确是在 arr 的 $[L, R]$ 范围上打爆气球，但是必须满足 arr 中 $L - 1$ 位置的气球没爆， $R + 1$ 位置的气球没爆，才能调用该函数。

如此一来，以「最后一个被打爆的气球的位置」进行可能性的枚举。

举个例子：arr = [2, 3, 5, 2, 1]

可能性枚举：

0位置的气球最后打爆。那么之前打过的气球范围是[1, 4]，也就是说在调用 f(1,4) 的时候是满足上述的条件的：可以认为0位置的气球没爆，5位置的气球没爆。
1位置的气球最后打爆。那么可以调用 f(0,0) 得到一个分数，调用该函数时可认为此时-1位置的气球没爆，分数为1，1位置的气球也没爆，分数为3，此时就得到了左边的得分 $f (0, 0)$ ；然后调用 f(2, 4) 得到一个分数；最终的得分就是 $f (0, 0) + f (2, 4) + 1 * a rr [1] * 1$ ，最后的 $1 * a rr [1] * 1$ 可理解为当左边没有气球的时候分数为1，右边没有气球的时候分数也为1，最后打爆1位置的气球得分就是 $1 * a rr [1] * 1$ 。
…

因为涉及到越界问题，可以将原数组 arr = [2, 3, 5, 2, 1] 处理成 arr‘ = [1, 2, 3, 5, 2, 1, 0]，也就是在最前面和最后面都添加一个1，那么「针对 arr 数组的 f(0,4) 的调用」等价于「调用 arr' 的 f(1, 5)」。

1.3 代码实现

暴力递归

public class BurstBalloons {
	public static int maxCoins(int[] arr) {
		//原始数组：[3, 2, 1, 3]
		//处理得到的help数组：[1, 3, 2, 1, 3, 1]
		int N = arr.length;
		int[] help = new int[N + 2];
		
		for (int i = 0; i < N; i++) {
			help[i + 1] = arr[i];
		}
		help[0] = 1;
		help[N + 1] = 1;
		
		return func(help, 1, N);
	}
	
	//暴力递归解法：超时
	//L-1位置和 R+1位置永不越界，且 L-1位置和R+1位置一定没爆
	//返回 arr 的 L到R范围上打爆所有气球，最大的得分
	public static int func(int[] arr, int L, int R) {
		if (L == R) { //只剩一个气球，打爆它
			//满足潜台词：左边的气球和右边的气球一定没爆
			return arr[L - 1] * arr[L] * arr[R + 1]; 
		}
		//尝试每一种情况，在L到R范围进行尝试：最后打爆的气球是什么位置
		//可能性1：L位置的气球最后打爆
		//调用func(arr, L + 1, R)这个子过程的时候，已经满足了潜台词，L位置和R+1位置没爆
		//打最后一个L位置的气球时，此时它的左边没打爆的是L-1位置，右边没打爆的是R+1位置
		int max = func(arr, L + 1, R) + arr[L - 1] * arr[L] * arr[R + 1];
		
		//可能性2：R位置的气球最后打爆
		max = Math.max(max, func(arr, L, R - 1) + arr[L - 1] * arr[R] * arr[R + 1])；

		//可能性3：尝试(L,R)范围的所有位置
		for (int i = L + 1; i < R; i++) {
			// i位置的气球最后打爆
			int left = func(arr, L, i - 1);
			int right = func(arr, i + 1, R);
			int last = arr[L - 1] * arr[i] * arr[R + 1];
			int cur = left + right + last;
			max = Math.max(max, cur);
		}
		return max;
	} 	
}

动态规划

public class BurstBalloons {
	public static int maxCoins(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		if (arr.length == 1) {
			return arr[0];
		}
		int N = arr.length;
		int[] help = new int[N + 2];
		help[0] = 1;
		help[N + 1] = 1;
		for (int i = 0; i < N; i++) {
			help[i + 1] = arr[i];
		}
		int[][] dp = new int[N + 2][N + 2];
		for (int i = 1; i <= N; i++) {
			dp[i][i] = help[i - 1] * help[i] * help[i + 1];
		}
		for (int L = N; L >= 1; L--) {
			for (int R = L + 1; R <= N; R++) {
				int ans = help[L - 1] * help[L] * help[R + 1] + dp[L + 1][R];
				ans = Math.max(ans, help[L - 1] * help[R] * help[R + 1] + dp[L][R - 1]);
				for (int i = L + 1; i < R; i++) {
					ans = Math.max(ans, help[L - 1] * help[i] * help[R + 1] + dp[L][i - 1] + dp[i + 1][R]);
				}
				dp[L][R] = ans;
			}
		}
		return dp[1][N];
	}
}

1.4 启示

本题尝试的方法是潜台词+最后一个打爆的气球，如果题目的得分是求被打爆气球的左边离它最近的打爆的气球和右边离它最近的打爆的气球最终得分，那就枚举「第一个打爆的气球位置」

启示：无论什么尝试的方法，都要满足可变参数的复杂度不要突破整型以上，通常有两种技巧：

设计潜台词。当设计的函数满足某些潜台词的情况下，有可能就不用管某些我需要的外部信息，比如本题中在规定了潜台词「 $L - 1$ 位置没爆， $R + 1$ 位置没爆」的前提下，就可以省下左侧信息的具体情况和右侧信息的具体情况
从尝试入手。可能性的展开方式。

2、Leetcode 546.移除盒子（困难）

2.1 题目描述

给出一些不同颜色的盒子 boxes ，盒子的颜色由不同的正数表示。

你将经过若干轮操作去去掉盒子，直到所有的盒子都去掉为止。每一轮你可以移除具有相同颜色的连续 k 个盒子（k >= 1），这样一轮之后你将得到 k * k 个积分。

返回 你能获得的最大积分和 。

示例1：

输入：boxes = [1,3,2,2,2,3,4,3,1]
输出：23
解释：
[1, 3, 2, 2, 2, 3, 4, 3, 1] 
----> [1, 3, 3, 4, 3, 1] (3*3=9 分) 
----> [1, 3, 3, 3, 1] (1*1=1 分) 
----> [1, 1] (3*3=9 分) 
----> [] (2*2=4 分)

示例2：

输入：boxes = [1,1,1]
输出：9

示例3：

输入：boxes = [1]
输出：1

2.2 思路分析

暴力递归

在 $L$ 到 $R$ 范围上移除盒子，但是不给这个范围左边和右边的信息是无法处理的，所以还是面对着一个外部信息如何简化的过程。

一种猜法：设计一个函数 int f(int[] arr, int L, int R, int k)，表示在 arr 的 L 到 R 范围上移除盒子，且在 arr 的左边有 k 个和 arr[L] 一样的数紧贴着 arr，在这种情况下移除 arr 的 L- k 到 R 范围上的盒子的最大积分是多少？

如何展开可能性呢？

举个例子：
在这里插入图片描述
对于该例子，就是在调用 $f (a rr, 21, 31, 5)$ 。

按理来说，对于前面的5个1，可以直接将这5个1单独消掉，不和紧挨着的后面的1一起消除，得分 $\times 5$ ，然后调用 $f (a rr, 21, 31, 0)$ 。但是通常这种可能性不考虑，因为连续的相同的数越多，一起消除得分就越高。

那么对于有效的可能性：

调用 $f (a rr, 22, 31, 6)$ ，也就是将前面的5个1和21位置的1合在一起；
调用 $f (a rr, 23, 31, 7)$ ，将前面的6个1和22位置的1合在一起；
… …

也就是说，要决定5个1是和后面的哪个位置一起消掉：

如果5个1和21位置的1一起消掉，则后面的过程调用 $f (a rr, 22, 31, 6)$ ；
如果5个1和22位置的1一起消掉，那么对于21位置的1，就要调用 $f (a rr, 21, 21, 0)$ ，因为它自己单独消掉，5个1贴着22位置的1，所以还要调用 $f (a rr, 22, 31, 5)$ ，整体就是 $f (a rr, 21, 21, 0) + f (a rr, 22, 31, 5)$ ；
如果选择和 23 位置的 1 一起消除，那么就是调用 $f (a rr, 21, 22, 0) + f (a rr, 23, 31, 5)$ ；
这5个1还可以和 26 位置的1 一起消，也可以跟着27位置的1一起小，还可以跟着 28 位置的1 一起消，跟着31位置的1一起消。将中间范围的数消除后就可以促成这种局面。

也就是说 可能性的枚举就是 5 个 1 和 (21, 31) 范围上的哪个位置的 1 一起消除，要么自己消除，要么和其他位置一起消除。

代码实现：

//在arr的L到R范围上消除，且前面紧跟着k个arr[L]这个数，返回所有东西都消掉的最大得分
public class RemoveBoxes {
	public static int func1(int[] arr, int L, int R, int K) {
		//无效范围
		if (L > R）return 0;
		
		//K个arr[L]值和L位置的值一起消掉，一共K+1个数一起消掉的
		//后续过程就是消除 L+1 到 R 范围上的数，前面一个数都没有了
		int ans = func1(arr, L + 1, R, 0) + (K + 1) * (K + 1);
		
		//前面的K个arr[L] 和 L 位置的数合并了，现在一共有K+1个arr[L]这个数
		for (int i = L + 1; i <= R; i++) {
			//如果i位置的数和arr[L]相等，则K+1个数和i位置的数一起消掉，先消除L+1到i-1范围上的数，然后K+1个数就和i位置的数挨着了
			//即是在枚举L+1到R范围上所有和arr[L]相等的位置
			if (arr[i] == arr[L]) { 
				ans = Math.max(ans, func1(arr, L + 1, i - 1, 0) + func1(arr, i, R, K + 1));
			}
		}
		return ans;
	}
}

记忆化搜索版本：

public class RemoveBoxes {
	public static int removeBoxes1(int[] boxes) {
		int N = boxes.length;
		int[][][] dp = new int[N][N][N];
		int ans = process1(boxes, 0, N - 1, 0, dp);
		return ans;
	}

	public static int process1(int[] boxes, int L, int R, int K, int[][][] dp) {
		if (L > R) {
			return 0;
		}
		if (dp[L][R][K] > 0) {
			return dp[L][R][K];
		}
		int ans = process1(boxes, L + 1, R, 0, dp) + (K + 1) * (K + 1);
		for (int i = L + 1; i <= R; i++) {
			if (boxes[i] == boxes[L]) {
				ans = Math.max(ans, process1(boxes, L + 1, i - 1, 0, dp) + process1(boxes, i, R, K + 1, dp));
			}
		}
		dp[L][R][K] = ans;
		return ans;
	}
}

优化版本：只能优化常数项

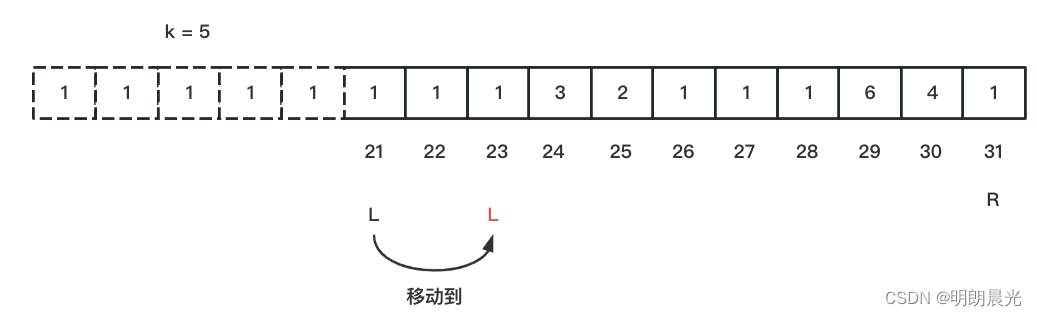
在这里插入图片描述
如果 L 到 R 范围上有连续的1，就将 L 移动到最后一个 1 的位置处，则此时：

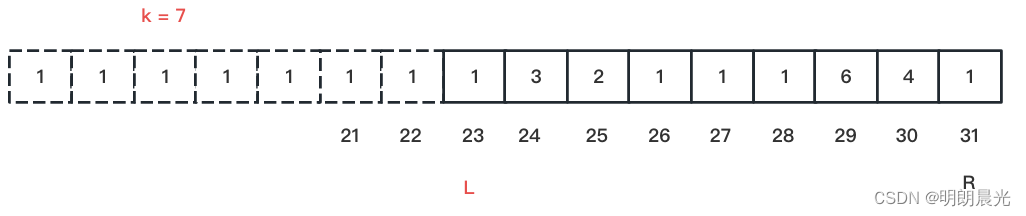
也就是说，如果开头有相同的，只保留一个，若中间有连续相同的则只尝试其中的第一个。也就是收，上述开头的 8 个1 只需要尝试和 26 位置的 1 一起消掉即可，因为26/27/28位置是连续的1，当来到该范围的时候，会自动去做最好的合并。

代码实现：

public class RemoveBoxes {
	public static int removeBoxes2(int[] boxes) {
		int N = boxes.length;
		int[][][] dp = new int[N][N][N];
		int ans = process2(boxes, 0, N - 1, 0, dp);
		return ans;
	}

	public static int process2(int[] boxes, int L, int R, int K, int[][][] dp) {
		if (L > R) {
			return 0;
		}
		if (dp[L][R][K] > 0) {
			return dp[L][R][K];
		}
		// 找到开头，
		// 1,1,1,1,1,5
		// 3 4 5 6 7 8   -> 下标
		//         !
		int last = L; //相同前缀中的最后一个位置
		while (last + 1 <= R && boxes[last + 1] == boxes[L]) {
			last++;
		}
		// K个1     (K + last - L) last
		int pre = K + last - L; //此时在last这个位置之前连续的arr[L]这个数的个数，即last之前相同的数合并到一起了，此时last这个位置的值还没和前面的(K+last-1)个数合在一起
		//可能性1：pre个1和last这个位置的1一起消掉
		int ans = (pre + 1) * (pre + 1) + process2(boxes, last + 1, R, 0, dp);
		//可能性2：和其他位置的数一起消掉
		//之所以从last+2位置开始尝试，是因为已经明确知道last+1位置的数不是arr[l]
		for (int i = last + 2; i <= R; i++) {
			if (boxes[i] == boxes[L] && boxes[i - 1] != boxes[L]) { //找到第一个和arr[l]相等的位置，连续的情况也只需要找到第一个位置
				ans = Math.max(ans, process2(boxes, last + 1, i - 1, 0, dp) + process2(boxes, i, R, pre + 1, dp));
			}
		}
		dp[L][R][K] = ans;
		return ans;
	}
}

2.3 代码实现

// 本题测试链接 : https://leetcode.com/problems/remove-boxes/
public class RemoveBoxes {
	//暴力递归版本
	// arr[L...R]消除，而且前面跟着K个arr[L]这个数
	// 返回：所有东西都消掉，最大得分
	public static int func1(int[] arr, int L, int R, int K) {
		if (L > R) {
			return 0;
		}
		int ans = func1(arr, L + 1, R, 0) + (K + 1) * (K + 1);
		
		// 前面的K个X，和arr[L]数，合在一起了，现在有K+1个arr[L]位置的数
		for (int i = L + 1; i <= R; i++) {
			if (arr[i] == arr[L]) {
				ans = Math.max(ans, func1(arr, L + 1, i - 1, 0) + func1(arr, i, R, K + 1));
			}
		}
		return ans;
	}
	
	//记忆化搜索版本
	public static int removeBoxes1(int[] boxes) {
		int N = boxes.length;
		int[][][] dp = new int[N][N][N];
		int ans = process1(boxes, 0, N - 1, 0, dp);
		return ans;
	}

	public static int process1(int[] boxes, int L, int R, int K, int[][][] dp) {
		if (L > R) {
			return 0;
		}
		if (dp[L][R][K] > 0) {
			return dp[L][R][K];
		}
		int ans = process1(boxes, L + 1, R, 0, dp) + (K + 1) * (K + 1);
		for (int i = L + 1; i <= R; i++) {
			if (boxes[i] == boxes[L]) {
				ans = Math.max(ans, process1(boxes, L + 1, i - 1, 0, dp) + process1(boxes, i, R, K + 1, dp));
			}
		}
		dp[L][R][K] = ans;
		return ans;
	}
	
	//动态规划版本
	public static int removeBoxes2(int[] boxes) {
		int N = boxes.length;
		int[][][] dp = new int[N][N][N];
		int ans = process2(boxes, 0, N - 1, 0, dp);
		return ans;
	}

	public static int process2(int[] boxes, int L, int R, int K, int[][][] dp) {
		if (L > R) {
			return 0;
		}
		if (dp[L][R][K] > 0) {
			return dp[L][R][K];
		}
		// 找到开头，
		// 1,1,1,1,1,5
		// 3 4 5 6 7 8
		//         !
		int last = L;
		while (last + 1 <= R && boxes[last + 1] == boxes[L]) {
			last++;
		}
		// K个1     (K + last - L) last
		int pre = K + last - L;
		int ans = (pre + 1) * (pre + 1) + process2(boxes, last + 1, R, 0, dp);
		for (int i = last + 2; i <= R; i++) {
			if (boxes[i] == boxes[L] && boxes[i - 1] != boxes[L]) {
				ans = Math.max(ans, process2(boxes, last + 1, i - 1, 0, dp) + process2(boxes, i, R, pre + 1, dp));
			}
		}
		dp[L][R][K] = ans;
		return ans;
	}
}

3、消除字符

3.1 题目描述

如果一个字符相邻的位置没有相同字符，那么这个位置的字符出现不能被消除。比如：“ab”，其中a和b都不能被消除。

如果一个字符相邻的位置有相同字符，就可以一起消除。比如:“abbbc”，中间一串的b是可以被消除的，消除之后剩下“ac”。某些字符如果消除了，剩下的字符认为重新靠在一起。

给定一个字符串，你可以决定每一步消除的顺序，目标是请尽可能多的消除字符，返回最少的剩余字符数量。

示例1：

"aacca",
如果先消掉最左侧的"aa"，那么将剩下"cca"；
然后把"cc"消掉，剩下的"a"将无法再消除，返回1。

如果先消掉中间的"cc"，那么将剩下"aaa"；
最后都消掉就一个字符也不剩了，返回0，这才是最优解。

示例2：

"baaccabb"
如果先消除最左侧的两个a，剩下"bccabb"；
如果再消除最左侧的两个c，剩下"babb"；
最后消除最右侧的两个b，剩下"ba"无法再消除，返回2。

而最优策略是：
先消除中间的两个c，剩下"baaabb"；
再消除中间的三个a，剩下"bbb"；
最后消除三个b，不留下任何字符，返回0，这才是最优解

3.2 思路分析

和“移除盒子”问题类似，设计一个函数 int f(L, R, has)，表示要在L到R范围上消掉字符，但是前面是否有arr[L]位置的字符跟着，这种情况下最少剩几个字符。

举例：
“aaaabckaaad”，如果在该字符串前面没有a跟着，则先找到前缀中最后一个a的位置是L+3，后续过程是 $f (L + 3, R, t r u e)$ ，表示在L+3到R范围上，且前面有a跟着的情况下，消掉字符最少剩几个。

“abckfbckaaad”，如果该字符串前面没有a跟着，此时就变成了L位置的a要和什么位置一起消掉，如果它不消，结果就是 1 + f(L+1, R, false)，其中的1就是这个不消的a；如果要消a，那就是先将L位置的a和后面的第一个a之间的字符"bckfbck"消掉，如果它能消成0，那L位置的a就可以和后续的a一起消，如果消不成0，那L位置的a就只能剩下。

3.3 代码实现

public class DeleteAdjacentSameCharacter {

	// 暴力解
	public static int restMin1(String s) {
		if (s == null) {
			return 0;
		}
		if (s.length() < 2) {
			return s.length();
		}
		int minLen = s.length();
		for (int L = 0; L < s.length(); L++) {
			for (int R = L + 1; R < s.length(); R++) {
				if (canDelete(s.substring(L, R + 1))) {
					minLen = Math.min(minLen, restMin1(s.substring(0, L) + s.substring(R + 1, s.length())));
				}
			}
		}
		return minLen;
	}

	public static boolean canDelete(String s) {
		char[] str = s.toCharArray();
		for (int i = 1; i < str.length; i++) {
			if (str[i - 1] != str[i]) {
				return false;
			}
		}
		return true;
	}

	// 优良尝试的暴力递归版本
	public static int restMin2(String s) {
		if (s == null) {
			return 0;
		}
		if (s.length() < 2) {
			return s.length();
		}
		char[] str = s.toCharArray();
		return process(str, 0, str.length - 1, false);
	}

	// str[L...R] 前面有没有跟着[L]字符，has表示， T 有 F 无
	// L,R,has
	// 最少能剩多少字符，消不了
	public static int process(char[] str, int L, int R, boolean has) {
		if (L > R) {
			return 0;
		}
		if (L == R) { //只剩一个字符，取决于前面是否有字符跟着
			return has ? 0 : 1;
		}
		int index = L;
		int K = has ? 1 : 0;
		while (index <= R && str[index] == str[L]) {
			K++;
			index++;
		}
		// index表示，第一个不是[L]字符的位置
		// K 只会 >=1
		// K > 1表示开始的一串能全部消掉
		int way1 = (K > 1 ? 0 : 1) + process(str, index, R, false);
		int way2 = Integer.MAX_VALUE;
		for (int split = index; split <= R; split++) {
			//找到后续的和[L]字符的位置相同的中的位置split，如果是连续的就找第一个
			if (str[split] == str[L] && str[split] != str[split - 1]) { 
				//如果开始连续的字符和split位置之间的字符能完全消掉，剩0个字符，则开始连续的字符和split的位置的字符一起消
				//否则不一起消，因为没法一起
				if (process(str, index, split - 1, false) == 0) { 
					way2 = Math.min(way2, process(str, split, R, K != 0));
				}
			}
		}
		return Math.min(way1, way2);
	}

	// 优良尝试的动态规划版本
	public static int restMin3(String s) {
		if (s == null) {
			return 0;
		}
		if (s.length() < 2) {
			return s.length();
		}
		char[] str = s.toCharArray();
		int N = str.length;
		int[][][] dp = new int[N][N][2];
		for (int i = 0; i < N; i++) {
			for (int j = 0; j < N; j++) {
				for (int k = 0; k < 2; k++) {
					dp[i][j][k] = -1;
				}
			}
		}
		return dpProcess(str, 0, N - 1, false, dp);
	}
	
	//虽然有三个可变参数，但是has是布尔类型，所以可以认为has=true的时候有一张表，has = false的时候有一张表
	//两张二维表
	public static int dpProcess(char[] str, int L, int R, boolean has, int[][][] dp) {
		if (L > R) {
			return 0;
		}
		int K = has ? 1 : 0;
		if (dp[L][R][K] != -1) {
			return dp[L][R][K];
		}
		int ans = 0;
		if (L == R) {
			ans = (K == 0 ? 1 : 0);
		} else {
			int index = L;
			int all = K;
			while (index <= R && str[index] == str[L]) {
				all++;
				index++;
			}
			int way1 = (all > 1 ? 0 : 1) + dpProcess(str, index, R, false, dp);
			int way2 = Integer.MAX_VALUE;
			for (int split = index; split <= R; split++) {
				if (str[split] == str[L] && str[split] != str[split - 1]) {
					if (dpProcess(str, index, split - 1, false, dp) == 0) {
						way2 = Math.min(way2, dpProcess(str, split, R, all > 0, dp));
					}
				}
			}
			ans = Math.min(way1, way2);
		}
		dp[L][R][K] = ans;
		return ans;
	}

	public static String randomString(int len, int variety) {
		char[] str = new char[len];
		for (int i = 0; i < len; i++) {
			str[i] = (char) ((int) (Math.random() * variety) + 'a');
		}
		return String.valueOf(str);
	}

	public static void main(String[] args) {
		int maxLen = 16;
		int variety = 3;
		int testTime = 100000;
		System.out.println("测试开始");
		for (int i = 0; i < testTime; i++) {
			int len = (int) (Math.random() * maxLen);
			String str = randomString(len, variety);
			int ans1 = restMin1(str);
			int ans2 = restMin2(str);
			int ans3 = restMin3(str);
			if (ans1 != ans2 || ans1 != ans3) {
				System.out.println(str);
				System.out.println(ans1);
				System.out.println(ans2);
				System.out.println(ans3);
				System.out.println("出错了！");
				break;
			}
		}
		System.out.println("测试结束");
	}
}