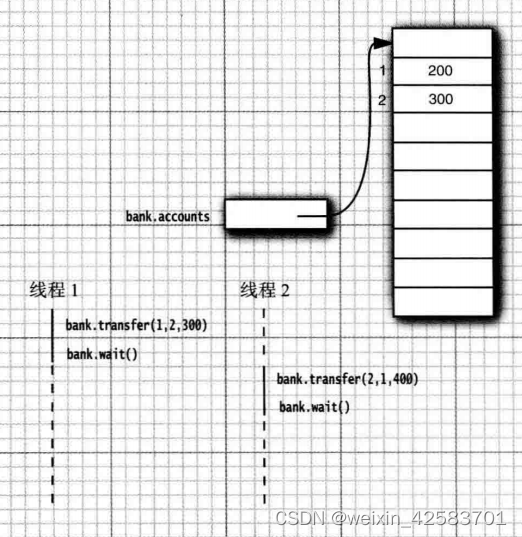
二叉树的基本概念:
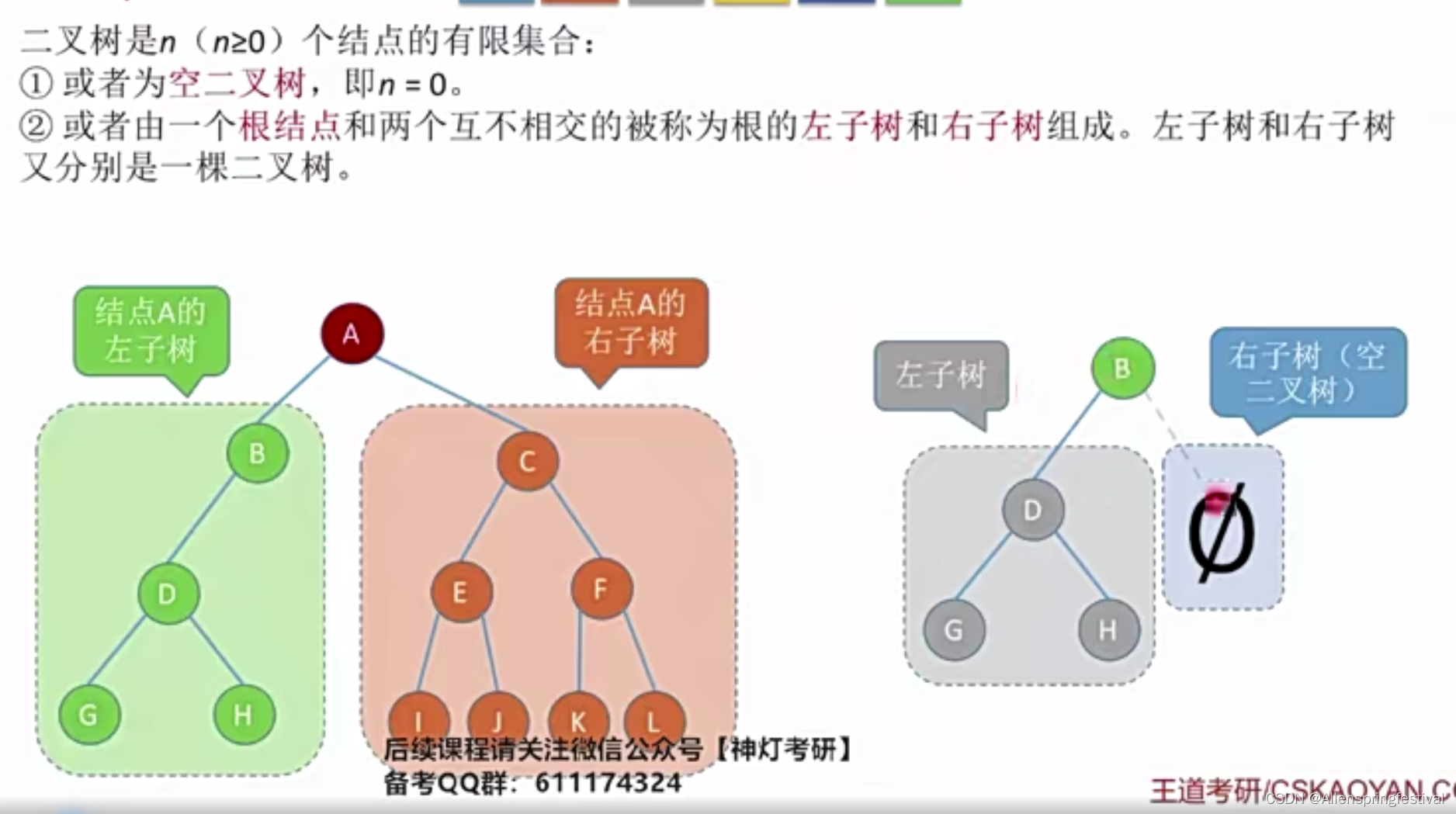
二叉树是递归定义的二叉树
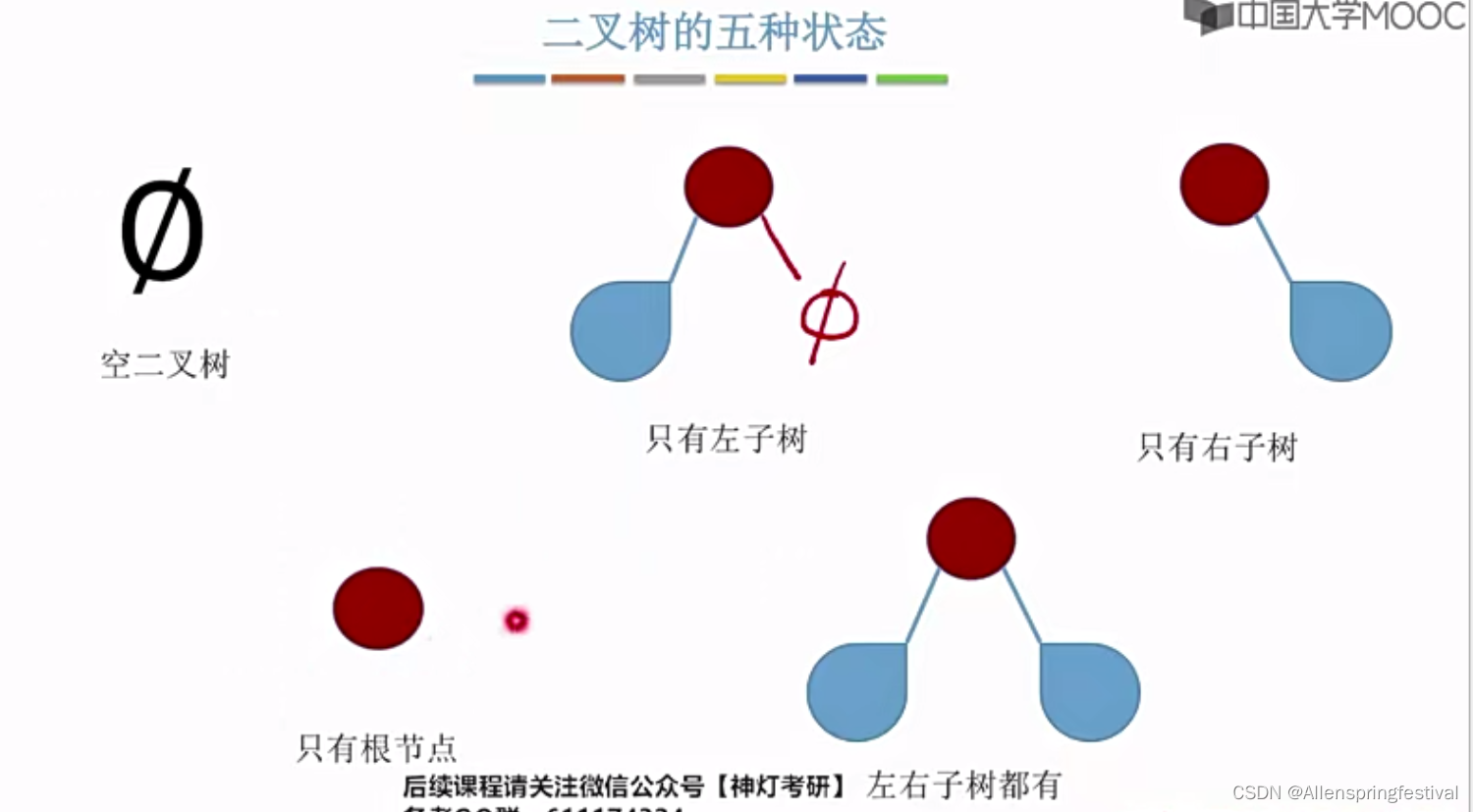
下面我们来看几个特殊的二叉树:

特点:
1)只有最后一层有叶子节点
2)不存在度为1的结点
3)按层序从1开始编号,结点i的左孩子为2i,右孩子为2i+1(这里的i是层数)
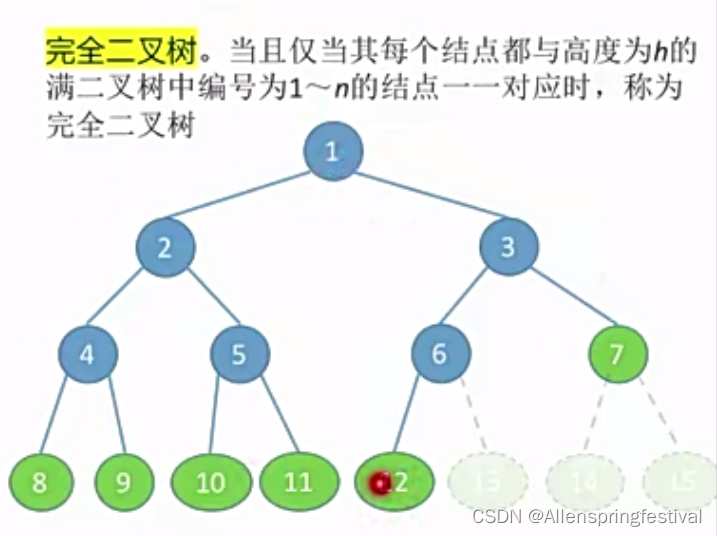
除了最后一层其他都满了。
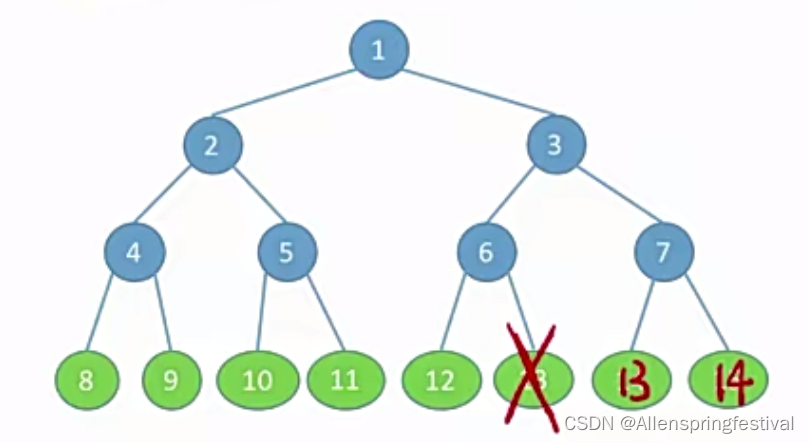
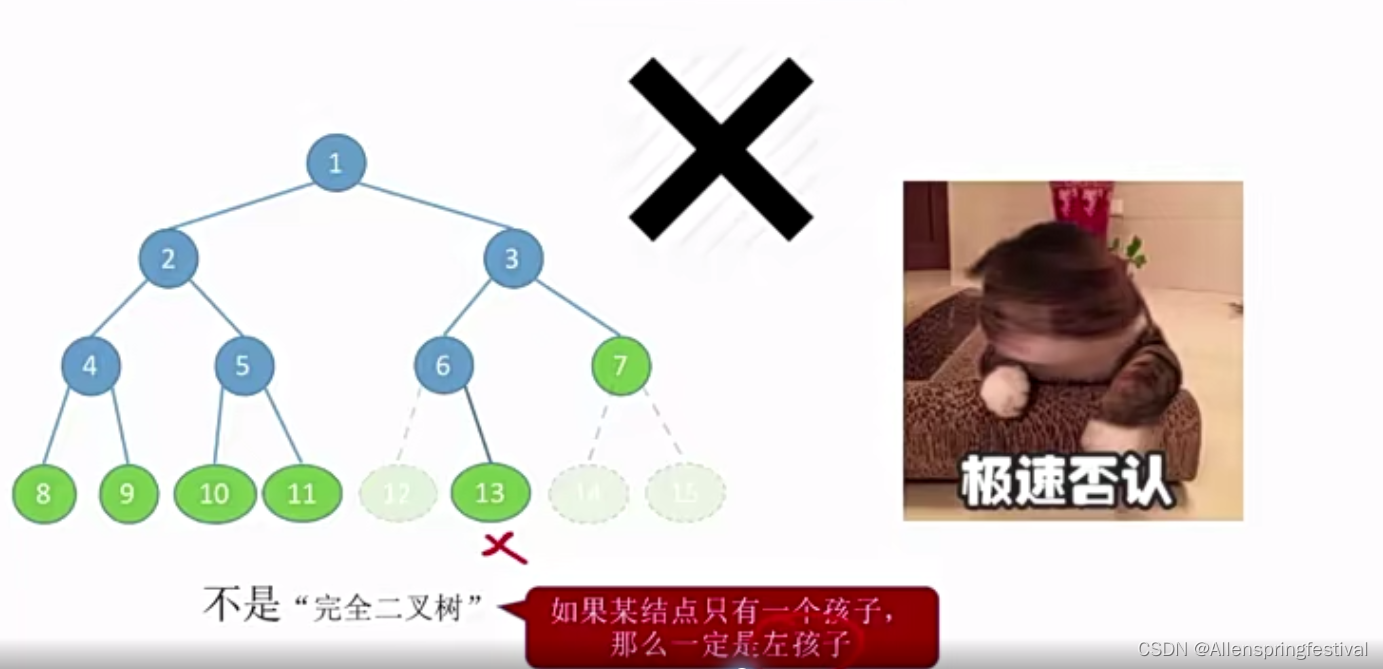
这样树的序号不能跟满二叉树一一对应,所以不是完全二叉树。

还满足一个特性,i<=n/2为分支节点,i>n/2为叶子节点。

1.左子树上所有节点的关键字均小于根节点的关键字
2.右子树上所有节点的关键字均大于根节点的关键字
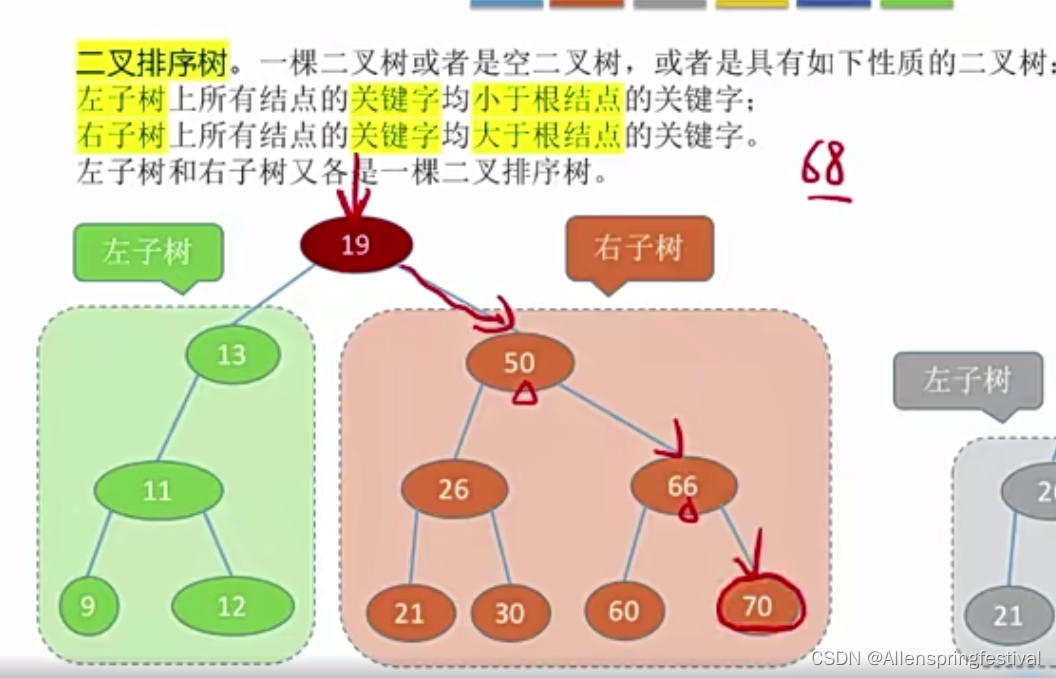
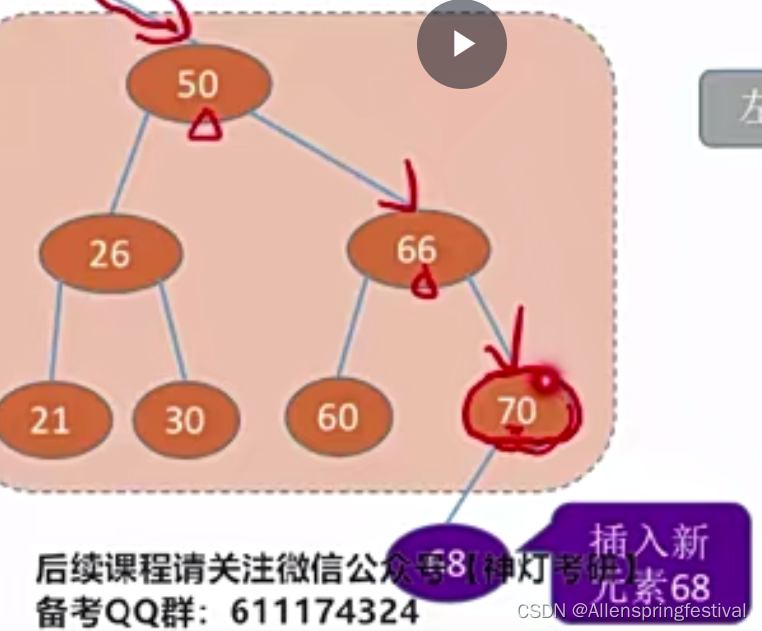
插入和查找元素很方便(操作后的树依然是二叉排序树)
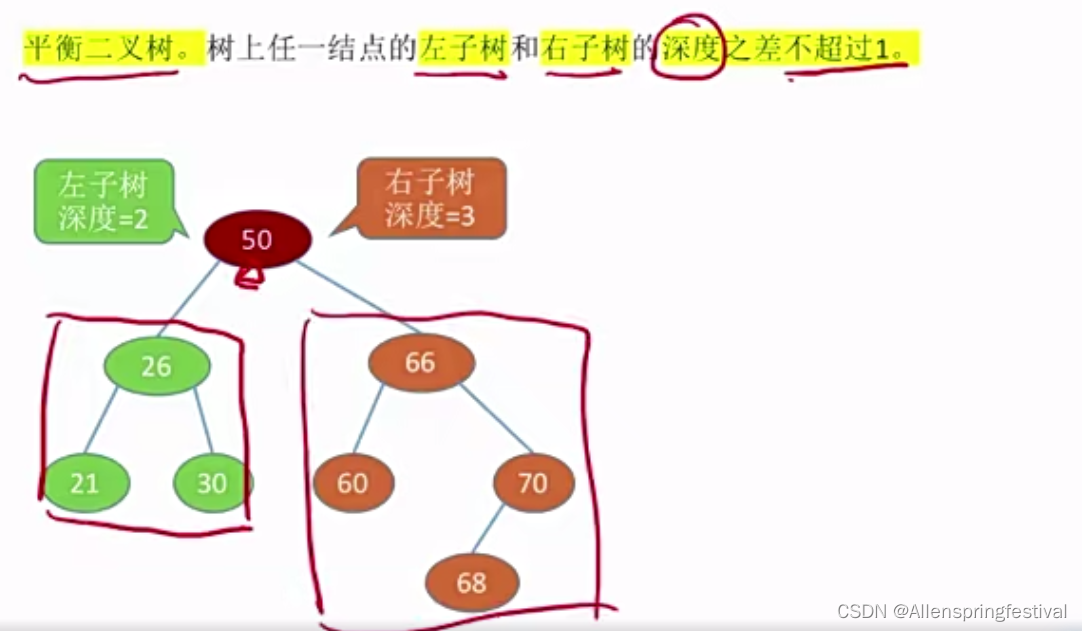
是
不是
平衡二叉树有更高的搜索效率(因为里面的关键字是由排序的)
平衡二叉树是丰满的胖胖的树。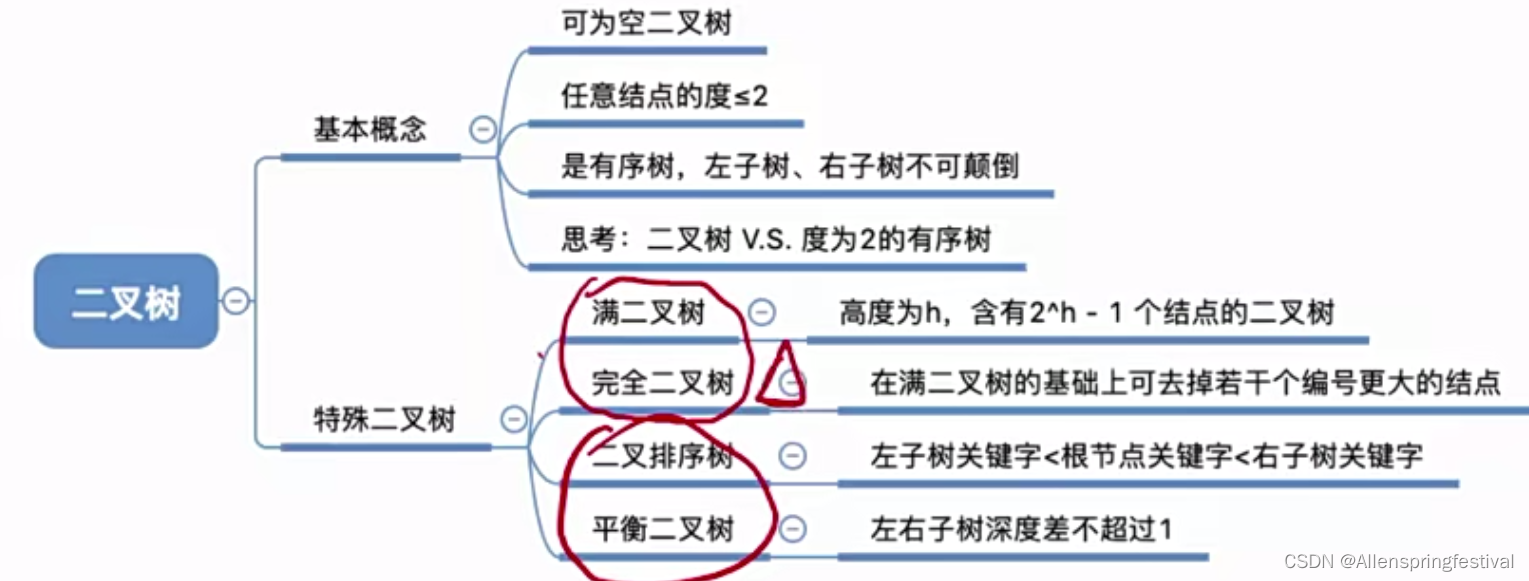





![[JavaEE初阶] 类加载机制](https://img-blog.csdnimg.cn/9198d6c8f0bd42d58b7669389dc12de8.png)