目录

1. Support Vector Machines

1.1 Example Dataset 1

1.2 SVM with Gaussian Kernels

1.2.1 Gaussian Kernel

1.2.2 Example Dataset 2

1.2.3 Example Dataset 3

2. Spam Classification

2.1 Preprocessing Emails

2.1.1 Vocabulary List

2.2 Extracting Features from Emails

2.3 Training SVM for Spam Classification

2.4 Top Predictors for Spam 

---

1. Support Vector Machines

内容：前半部分使用SVM对2D数据集进行应用，后半部分使用SVM来构建垃圾邮件分类器。

1.1 Example Dataset 1

内容：使用线性内核函数的SVM，调整参数C（=1/λ）的大小，并进行观察。

main.py

from scipy.io import loadmat  # 读取.mat文件
import pandas as pd  # 数据分析

res = loadmat('ex6data1.mat')
data = pd.DataFrame(res['X'], columns=['x1', 'x2'])
data['y'] = res['y']
print(data.head())

            x1        x2   y
0  1.9643  4.5957  1
1  2.2753  3.8589  1
2  2.9781  4.5651  1
3  2.9320  3.5519  1
4  3.5772  2.8560  1

A. 可视化数据

plot.py

import matplotlib.pyplot as plt

def plotData(data):
    filter_pos = data['y'].isin([1])
    filter_neg = data['y'].isin([0])
    positive = data[filter_pos]
    negative = data[filter_neg]
    fig, ax = plt.subplots(figsize=(8, 6))
    ax.scatter(positive['x1'], positive['x2'], marker='x', c='r', label='Positive')
    ax.scatter(negative['x1'], negative['x2'], marker='o', c='b', label='Negative')
    ax.set_xlabel('x1')
    ax.set_ylabel('x2')
    ax.legend()
    plt.show()
    return fig, ax

main.py

from scipy.io import loadmat  # 读取.mat文件
import pandas as pd  # 数据分析
from plot import *  # 数据可视化

res = loadmat('ex6data1.mat')
data = pd.DataFrame(res['X'], columns=['x1', 'x2'])
data['y'] = res['y']
plotData(data)

B. 训练线性SVM（带线性内核函数）

linearSVM.py

from sklearn import svm  # 机器学习

def linearSVM(data, C_number):
    # LinearSVC(C,max_iter, loss)
    # C:惩罚参数(1/λ),max_iter:最大迭代次数
    # loss:指定损失函数,“hinge”是标准的SVM损失
    svc = svm.LinearSVC(C=C_number, loss='hinge', max_iter=10000)
    # svc.fit(X,y) 根据给定的训练数据拟合SVM模型
    # svc.score(X,y) 返回给定测试数据和标签的平均精确度
    svc.fit(data[['x1', 'x2']], data['y'])
    print(svc.score(data[['x1', 'x2']], data['y']))  # 0.9803921568627451

main.py

from scipy.io import loadmat  # 读取.mat文件
import pandas as pd  # 数据分析
from linearSVM import *  # 线性SVM

res = loadmat('ex6data1.mat')
data = pd.DataFrame(res['X'], columns=['x1', 'x2'])
data['y'] = res['y']
C = 1  # 惩罚项
linearSVM(data, C)

C. 可视化决策边界

linearSVM.py

from sklearn import svm  # 机器学习
import numpy as np
import pandas as pd
from plot import *  # 绘制决策边界

def linearSVM(data, C_number):
    # LinearSVC(C,max_iter, loss)
    # C:惩罚参数(1/λ),max_iter:最大迭代次数
    # loss:指定损失函数,“hinge”是标准的SVM损失
    svc = svm.LinearSVC(C=C_number, loss='hinge', max_iter=10000)
    # svc.fit(X,y) 根据给定的训练数据拟合SVM模型
    # svc.score(X,y) 返回给定测试数据和标签的平均精确度
    svc.fit(data[['x1', 'x2']], data['y'])
    x1, x2 = findDecisionBoundary(svc, 0, 4, 1.5, 5, 2 * 10 ** -3)  # 寻找决策边界
    plotDecisionBoundary(data, x1, x2)

def findDecisionBoundary(svc, x1min, x1max, x2min, x2max, dis):
    x1 = np.linspace(x1min, x1max, 1000)
    x2 = np.linspace(x2min, x2max, 1000)
    coordinates = [(x, y) for x in x1 for y in x2]
    # print(len(coordinates))  # 1000*1000=1,000,000
    x_cord, y_cord = zip(*coordinates)  # 解压
    # print(len(x_cord)) #1,000,000
    points = pd.DataFrame({'x1': x_cord, 'x2': y_cord})
    # svc.decision_function(X) 样本X到分离超平面的距离
    points['val'] = svc.decision_function(points[['x1', 'x2']])
    decision = points[np.abs(points['val']) < dis]  # 这些点可以构成一个决策边界（想法:近乎贴近超平面）
    return decision.x1, decision.x2

plot.py

import matplotlib.pyplot as plt

# 数据可视化
def plotData(data):
    filter_pos = data['y'].isin([1])
    filter_neg = data['y'].isin([0])
    positive = data[filter_pos]
    negative = data[filter_neg]
    fig, ax = plt.subplots(figsize=(8, 6))
    ax.scatter(positive['x1'], positive['x2'], marker='x', c='r', label='Positive')
    ax.scatter(negative['x1'], negative['x2'], marker='o', c='b', label='Negative')
    ax.set_xlabel('x1')
    ax.set_ylabel('x2')
    return fig, ax

# 绘制决策边界
def plotDecisionBoundary(data, x1, x2):
    fig, ax = plotData(data)
    ax.scatter(x1, x2, c='g', s=10, label='Boundary')
    ax.set_title('SVM Decision Boundary with C=1')
    ax.legend()
    plt.show()

调整参数C（=1/λ）的值：C=100

main.py

C = 100  # 惩罚项

linearSVM.py（部分修改）

def linearSVM(data, C_number):
    svc = svm.LinearSVC(C=C_number, loss='hinge', max_iter=1000)
    svc.fit(data[['x1', 'x2']], data['y'])
    print(svc.score(data[['x1', 'x2']], data['y']))  # 0.9803921568627451
    x1, x2 = findDecisionBoundary(svc, 0, 4, 1.5, 5, 2 * 10 ** -3)  # 寻找决策边界
    plotDecisionBoundary(data, x1, x2)

观察：随着C的增大，可以得到一个完美的分类结果，但是创建了一个不再适合数据的决策边界。

1.2 SVM with Gaussian Kernels

内容：我们会使用带有高斯内核函数的SVM来处理非线性分类。

1.2.1 Gaussian Kernel

内容：高斯核函数是一个表示数据间“距离”的相似度函数，参数σ可以决定相似度下降到0的快慢程度。

gaussianKernel.py

import numpy as np

def gaussianKernel(x1, x2, sigma):
    return np.exp(-np.sum((x1 - x2) ** 2) / (2 * sigma ** 2))

x1 = np.array([1, 2, 1])
x2 = np.array([0, 4, -1])
sigma = 2
print(gaussianKernel(x1, x2, sigma))

 0.32465246735834974

1.2.2 Example Dataset 2

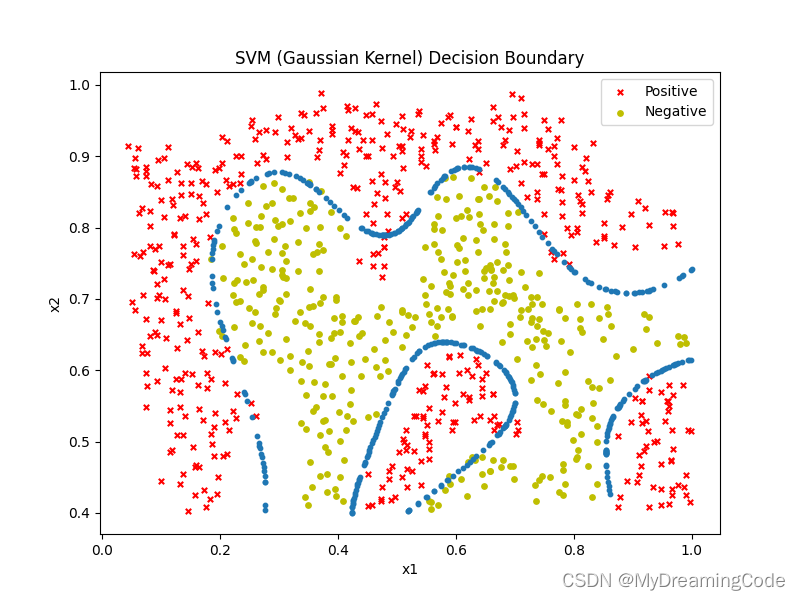
内容：在数据集2上使用带高斯核函数的SVM找到决策边界。

main.py

from scipy.io import loadmat
import pandas as pd

raw_data = loadmat('ex6data2.mat')
data = pd.DataFrame(raw_data['X'], columns=['x1', 'x2'])
data['y'] = raw_data['y']
print(data.head())

               x1              x2  y
0  0.107143  0.603070  1
1  0.093318  0.649854  1
2  0.097926  0.705409  1
3  0.155530  0.784357  1
4  0.210829  0.866228  1

数据可视化

plot.py

import matplotlib.pyplot as plt

def plotData(data, ax):
    filter_pos = data['y'].isin([1])
    filter_neg = data['y'].isin([0])
    positive = data[filter_pos]
    negative = data[filter_neg]
    ax.scatter(positive['x1'], positive['x2'], c='r', s=15, marker='x', label='Positive')
    ax.scatter(negative['x1'], negative['x2'], c='y', s=15, label='Negative')
    ax.set_xlabel('x1')
    ax.set_ylabel('x2')
    ax.legend()

main.py

from scipy.io import loadmat
import pandas as pd
import matplotlib.pyplot as plt
from plot import *  # 绘制数据

raw_data = loadmat('ex6data2.mat')
data = pd.DataFrame(raw_data['X'], columns=['x1', 'x2'])
data['y'] = raw_data['y']
fig, ax = plt.subplots(figsize=(8, 6))
plotData(data, ax)
plt.show()

使用高斯核函数

main.py

from scipy.io import loadmat
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import svm
from plot import *  # 绘制数据

raw_data = loadmat('ex6data2.mat')
data = pd.DataFrame(raw_data['X'], columns=['x1', 'x2'])
data['y'] = raw_data['y']
# gamma:核函数系数
# probability:是否启用概率估计
svc = svm.SVC(C=100, gamma=10, probability=True)
svc.fit(data[['x1', 'x2']], data['y'])
print(svc.score(data[['x1', 'x2']], data['y']))

0.9698725376593279

foundDecisionBoundary.py

import numpy as np
import pandas as pd

def findDecisionBoundary(svc, x1_min, x1_max, x2_min, x2_max, dist):
    x1 = np.linspace(x1_min, x1_max, 1000)
    x2 = np.linspace(x2_min, x2_max, 1000)
    cordinates = [(x, y) for x in x1 for y in x2]
    x_cord, y_cord = zip(*cordinates)
    points = pd.DataFrame({'x1': x_cord, 'x2': y_cord})
    points['val'] = svc.decision_function(points[['x1', 'x2']])
    decision = points[np.abs(points['val']) < dist]
    return decision.x1, decision.x2

main.py

from scipy.io import loadmat
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import svm
from plot import *  # 绘制数据
from foundDecisionBoundary import *  # 决策边界

raw_data = loadmat('ex6data2.mat')
data = pd.DataFrame(raw_data['X'], columns=['x1', 'x2'])
data['y'] = raw_data['y']
# gamma:核函数系数
# probability:是否启用概率估计
svc = svm.SVC(C=100, gamma=10, probability=True)
svc.fit(data[['x1', 'x2']], data['y'])
x1, x2 = findDecisionBoundary(svc, 0, 1, 0.4, 1, 2 * 10 ** -3)
fig, ax = plt.subplots(figsize=(8, 6))
plotData(data, ax)
ax.scatter(x1, x2, s=10)
ax.set_title('SVM (Gaussian Kernel) Decision Boundary')
plt.show()

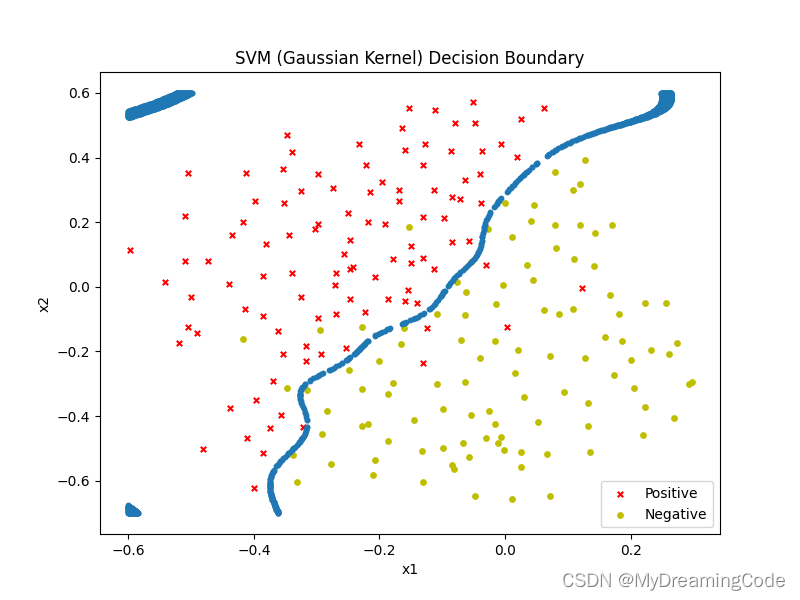
1.2.3 Example Dataset 3

内容：根据验证集，我们可以为SVM找到最优的C和σ参数，候选值为[0.01,0.03,0.1,0.3,1,3,10,30,100]。

main.py

from scipy.io import loadmat
import pandas as pd
import matplotlib.pyplot as plt
from plot import *  # 绘制数据

raw_data = loadmat('ex6data3.mat')
X, y, Xval, yval = raw_data['X'], raw_data['y'].ravel(), raw_data['Xval'], raw_data['yval'].ravel()
data = pd.DataFrame(X, columns=['x1', 'x2'])
data['y'] = y
print(data.head())
fig, ax = plt.subplots(figsize=(8, 6))
plotData(data, ax)
plt.show()

                x1             x2  y
0 -0.158986  0.423977  1
1 -0.347926  0.470760  1
2 -0.504608  0.353801  1
3 -0.596774  0.114035  1
4 -0.518433 -0.172515  1

 

A. 找到最优的参数C和σ

fitParam.py

from sklearn import svm

def fitParam(X, y, Xval, yval):
    C_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
    gamma_values = [0.01, 0.03, 0.1, 0.3, 1, 3, 10, 30, 100]
    best_score = 0
    best_params = {'C': None, 'gamma': None}
    for C in C_values:
        for gamma in gamma_values:
            svc = svm.SVC(C=C, gamma=gamma)
            svc.fit(X, y)
            score = svc.score(Xval, yval)
            if score > best_score:
                best_score = score
                best_params['C'] = C
                best_params['gamma'] = gamma
    return best_score, best_params

main.py

from scipy.io import loadmat
import pandas as pd
from fitParam import *  # 找到最优参数

raw_data = loadmat('ex6data3.mat')
X, y, Xval, yval = raw_data['X'], raw_data['y'].ravel(), raw_data['Xval'], raw_data['yval'].ravel()
data = pd.DataFrame(X, columns=['x1', 'x2'])
data['y'] = y
best_score, best_params = fitParam(X, y, Xval, yval)
print(best_score, best_params)

0.965 {'C': 0.3, 'gamma': 100}

main.py

from scipy.io import loadmat
import pandas as pd
from sklearn import svm  # 支持向量机
import matplotlib.pyplot as plt
from plot import *  # 绘制数据
from fitParam import *  # 找到最优参数
from foundDecisionBoundary import *  # 决策边界

raw_data = loadmat('ex6data3.mat')
X, y, Xval, yval = raw_data['X'], raw_data['y'].ravel(), raw_data['Xval'], raw_data['yval'].ravel()
data = pd.DataFrame(X, columns=['x1', 'x2'])
data['y'] = y
best_score, best_params = fitParam(X, y, Xval, yval)
svc = svm.SVC(C=best_params['C'], gamma=best_params['gamma'])
svc.fit(X, y)
x1, x2 = findDecisionBoundary(svc, -0.6, 0.3, -0.7, 0.6, 2 * 10 ** -3)
fig, ax = plt.subplots(figsize=(8, 6))
plotData(data, ax)
ax.scatter(x1, x2, s=10)
ax.set_title('SVM (Gaussian Kernel) Decision Boundary')
plt.show()

2. Spam Classification

内容：使用SVM来构建垃圾邮件过滤器。

2.1 Preprocessing Emails

内容：完成预处理邮件信息，使其更好为SVM所应用。比如：全部小写化、移除HTML标签、将所有URL统称为httpaddr、将所有邮件地址统称为emailaddr、将所有数字统称为number、将所有钱数统称为dollar、词干提取、移除标点符号以及非文字，将制表符、换行，多个空格统一为一个空格符等。

2.1.1 Vocabulary List

内容：

• 预处理好的邮件。
• 词汇列表：可以选择在垃圾语料库中至少出现过100次的这些单词，因为如果出现的次数较少，则可能会出现过拟合的情况。每个单词在词汇列表中都有对应的索引。
• 映射：将预处理好的邮件中的单词与词汇列表中的单词进行对比，如果是一样的，则返回相应索引值，如果未在索引表中出现，则跳过。

2.2 Extracting Features from Emails

内容： 将邮件转化成特征向量，特征向量的维度n即为词汇列表的长度。Xi∈{0,1}，Xi=0表示词汇表中的第 i 个单词在邮件中未出现，Xi=1表示词汇表中的第 i 个单词在邮件中出现。此例中特征向量长为1899，有45个非零项。

2.3 Training SVM for Spam Classification

内容：处理好的训练集有4000个邮件（含垃圾和非垃圾邮件），处理好的测试集有1000个邮件。使用SVM对其进行分类，垃圾邮件为y=1，非垃圾邮件为y=0。

main.py

from scipy.io import loadmat

rawTrainData = loadmat('spamTrain.mat')
rawTestData = loadmat('spamTest.mat')
X, y, Xtest, ytest = rawTrainData['X'], rawTrainData['y'].ravel(), rawTestData['Xtest'], rawTestData['ytest'].ravel()
print(X.shape, y.shape, Xtest.shape, ytest.shape)
# (4000, 1899) (4000,) (1000, 1899) (1000,)

说明：1899表示这封邮件的单词在词汇表（1899个词）中有无出现，出现则为1，未出现则为0。

main.py

from scipy.io import loadmat
from sklearn import svm
import numpy as np

rawTrainData = loadmat('spamTrain.mat')
rawTestData = loadmat('spamTest.mat')
X, y, Xtest, ytest = rawTrainData['X'], rawTrainData['y'].ravel(), rawTestData['Xtest'], rawTestData['ytest'].ravel()
svc = svm.SVC()
svc.fit(X, y)
# round()设置保留几位小数
print('Training accuracy={0}%'.format(np.round(svc.score(X, y) * 100, 2)))
print('Test accuracy={0}%'.format(np.round(svc.score(Xtest, ytest) * 100, 2)))

Training accuracy=99.32%
Test accuracy=98.7%

2.4 Top Predictors for Spam 

内容：垃圾邮件的主要预测因素。

main.py

from scipy.io import loadmat
from sklearn import svm
import numpy as np
import pandas as pd

rawTrainData = loadmat('spamTrain.mat')
rawTestData = loadmat('spamTest.mat')
X, y, Xtest, ytest = rawTrainData['X'], rawTrainData['y'].ravel(), rawTestData['Xtest'], rawTestData['ytest'].ravel()
svc = svm.SVC()
svc.fit(X, y)
# 创建单位矩阵
kw = np.eye(1899)
spam_val = pd.DataFrame({'idx': range(1899)})
spam_val['isspam'] = svc.decision_function(kw)
# pd.describe()返回统计变量
print(spam_val['isspam'].describe())
# count:数量统计 mean:均值 std:标准差 min:最小值

count    1899.000000
mean       -0.110039
std         0.049094
min        -0.428396
25%        -0.131213
50%        -0.111985
75%        -0.091973
max         0.396286
Name: isspam, dtype: float64

main.py

from scipy.io import loadmat
from sklearn import svm
import numpy as np
import pandas as pd

rawTrainData = loadmat('spamTrain.mat')
rawTestData = loadmat('spamTest.mat')
X, y, Xtest, ytest = rawTrainData['X'], rawTrainData['y'].ravel(), rawTestData['Xtest'], rawTestData['ytest'].ravel()
svc = svm.SVC()
svc.fit(X, y)
# 创建单位矩阵
kw = np.eye(1899)
spam_val = pd.DataFrame({'idx': range(1899)})
spam_val['isspam'] = svc.decision_function(kw)
decision = spam_val[spam_val['isspam'] > 0]
print(decision)

            idx    isspam
155    155  0.095529
173    173  0.066666
297    297  0.396286
351    351  0.023785
382    382  0.030317
476    476  0.042474
478    478  0.057344
529    529  0.060692
537    537  0.008558
680    680  0.109643
697    697  0.003269
738    738  0.092561
774    774  0.181496
791    791  0.040396
1008  1008  0.012187
1088  1088  0.132633
1101  1101  0.002832
1120  1120  0.003076
1163  1163  0.072045
1178  1178  0.012122
1182  1182  0.015656
1190  1190  0.232788
1263  1263  0.160806
1298  1298  0.044018
1372  1372  0.019640
1397  1397  0.218337
1399  1399  0.018762
1460  1460  0.001859
1467  1467  0.002822
1519  1519  0.001654
1661  1661  0.003775
1721  1721  0.057241
1740  1740  0.034107
1795  1795  0.125143
1823  1823  0.002071
1829  1829  0.002630
1851  1851  0.030662
1892  1892  0.052786
1894  1894  0.101613

main.py （词汇列表）

import pandas as pd

# sep正则
voc = pd.read_csv('vocab.txt', header=None, names=['idx', 'voc'], sep='\t')
print(voc.head())

    idx    voc
0    1     aa
1    2     ab
2    3   abil
3    4    abl
4    5  about

输出敏感（容易在垃圾邮件中出现的）词汇

main.py

from scipy.io import loadmat
from sklearn import svm
import numpy as np
import pandas as pd

rawTrainData = loadmat('spamTrain.mat')
rawTestData = loadmat('spamTest.mat')
X, y, Xtest, ytest = rawTrainData['X'], rawTrainData['y'].ravel(), rawTestData['Xtest'], rawTestData['ytest'].ravel()
svc = svm.SVC()
svc.fit(X, y)
# 创建单位矩阵
kw = np.eye(1899)
spam_val = pd.DataFrame({'idx': range(1899)})
spam_val['isspam'] = svc.decision_function(kw)
decision = spam_val[spam_val['isspam'] > 0]
# sep正则
voc = pd.read_csv('vocab.txt', header=None, names=['idx', 'voc'], sep='\t')
spamvoc = voc.loc[decision['idx']]
print(spamvoc)

           idx         voc
155    156    basenumb
173    174       below
297    298       click
351    352     contact
382    383      credit
476    477      dollar
478    479  dollarnumb
529    530       email
537    538       encod
680    681        free
697    698       futur
738    739    guarante
774    775        here
791    792        hour
1008  1009      market
1088  1089        nbsp
1101  1102    nextpart
1120  1121     numbera
1163  1164       offer
1178  1179         opt
1182  1183       order
1190  1191         our
1263  1264       pleas
1298  1299       price
1372  1373      receiv
1397  1398       remov
1399  1400       repli
1460  1461          se
1467  1468         see
1519  1520      sincer
1661  1662        text
1721  1722    transfer
1740  1741        type
1795  1796       visit
1823  1824      websit
1829  1830      welcom
1851  1852        will
1892  1893         you
1894  1895        your