1 RSA介绍
- RSA是一种非对称加密算法,即加密和解密时用到的密钥不同。
- 加密密钥是公钥,可以公开;解密密钥是私钥,必须保密保存。
- 基于一个简单的数论事实:两个大质数相乘很容易,但想要对其乘积进行因式分解却极其困难,因此可以将乘积公开作为加密密钥,即公钥;而两个大质数组合成私钥。
2 密钥对的生成
step 1 生成N(公钥和私钥的一部分)
首先选取两个互为质数的数
p
p
p和
q
q
q(
p
≠
q
,
g
c
d
(
p
,
q
)
=
1
p\neq q, gcd(p, q)=1
p=q,gcd(p,q)=1),于是:
N
=
p
∗
q
N = p * q
N=p∗q
step 2 生成L
根据欧拉函数,不大于 N N N且与 N N N互质的数是 p − 1 p-1 p−1和 q − 1 q-1 q−1两个数的最小公倍数:
L = [ p − 1 , q − 1 ] = ( p − 1 ) ( q − 1 ) L = [p-1, q-1] = (p-1)(q-1) L=[p−1,q−1]=(p−1)(q−1)
互质数 p p p和 q q q不能太小,如果他们足够大,那么根据目前的计算机技术和其他工具,至今也没能从 N N N分解出 p p p和 q q q。也就是说,只要密钥长度 N N N足够大(1024足够),基本上不可能从公钥信息推出私钥信息。
step 3 生成E(加密密钥)
满足如下两个条件:
1 < E < L 1 < E < L 1<E<L
g c d ( E , L ) = 1 gcd(E, L) = 1 gcd(E,L)=1
g c d ( E , L ) = 1 gcd(E, L) = 1 gcd(E,L)=1保证 E E E和 L L L最大公因数为1(互质),因此保证step 4生成解密密钥 D D D时,一定存在 D D D满足条件。
step 4 生成D(解密密钥)
满足如下两个条件:
1 < D < L 1 < D < L 1<D<L
( E ∗ D ) m o d L = 1 (E * D) mod L = 1 (E∗D)modL=1
3 加密解密过程
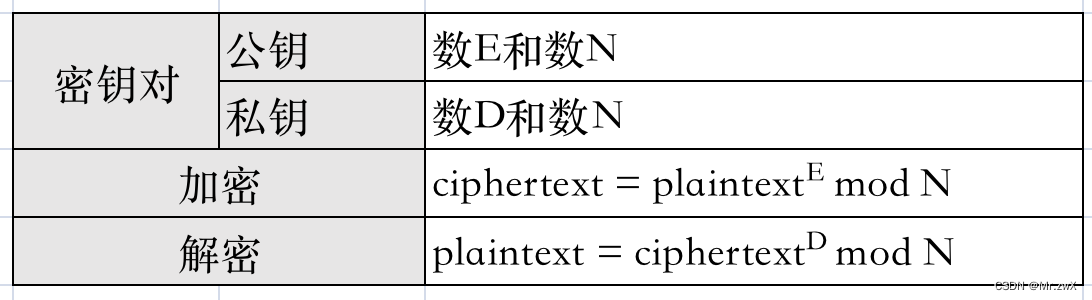
另外,密钥对为: ( E , D , N ) (E, D, N) (E,D,N)。
4 计算示例
明文信息为
p
l
a
i
n
t
e
x
t
=
85
,
E
=
7
,
p
=
11
,
q
=
13.
plaintext=85,E=7,p=11,q=13.
plaintext=85,E=7,p=11,q=13.
生成密钥对
step 1:
N
=
p
∗
q
=
11
∗
13
=
143
N=p*q=11*13=143
N=p∗q=11∗13=143
step 2:
L
=
(
p
−
1
)
(
q
−
1
)
=
10
∗
12
=
120
L=(p-1)(q-1)=10*12=120
L=(p−1)(q−1)=10∗12=120
step 3:
(
E
∗
D
)
m
o
d
L
=
1
⇒
(
7
∗
D
)
m
o
d
120
=
1
⇒
D
=
103
(E*D)modL=1 \Rightarrow (7*D)mod120=1 \Rightarrow D=103
(E∗D)modL=1⇒(7∗D)mod120=1⇒D=103
加密
c
y
p
h
e
r
t
e
x
t
=
p
l
a
i
n
t
e
x
t
E
m
o
d
N
=
8
5
7
m
o
d
143
=
123
cyphertext = plaintext^E mod N=85^7mod143=123
cyphertext=plaintextEmodN=857mod143=123
解密
p
l
a
i
n
t
e
x
t
=
c
y
p
h
e
r
t
e
x
t
D
m
o
d
143
=
12
3
103
m
o
d
143
=
85
plaintext = cyphertext^D mod 143=123^{103}mod143=85
plaintext=cyphertextDmod143=123103mod143=85