目录
1.回溯法
2.集合的幂集本质问题
3.集合的幂集
(1)集合
(2)求解集合的幂集
(3)算法描述
(4)算法实现
(5)算法拓展
1.回溯法
- 回溯法也是设计递归过程的一种重要方法,求解过程实质上是先序遍历一棵“状态树”的过程。
- 回溯法的应用
- 九宫格问题
- 八皇后问题
- 数独问题
- 求集合的幂集问题
2.集合的幂集本质问题
提示:如果读者学习过《算法设计与分析》的话,那么应该很清楚,其中有一类问题是可以使用分治法进行求解的,那什么是分治法呢?
- 分治法:就是将原问题划分若干个性质相同的小问题,并对划分的子问题进行求解。
- 分治过程:
- 将一个问题划分为同一类型的若干子问题,子问题最好规模相同。
- 对这些子问题求解。
- 合并这些子问题的解,以得到原始问题的答案。
3.集合的幂集
(1)集合
提示:集合的幂集就是集合A的所有子集所组成的集合。
题目:要求求n个元素的集合的幂集!
假设这里有三个元素:A={1,2,3},那么集合A的幂集?
ρ(A)={{1,2,3},{1,2},{1,3},{1},{2,3},{2},{3},Φ}
如下图所示:
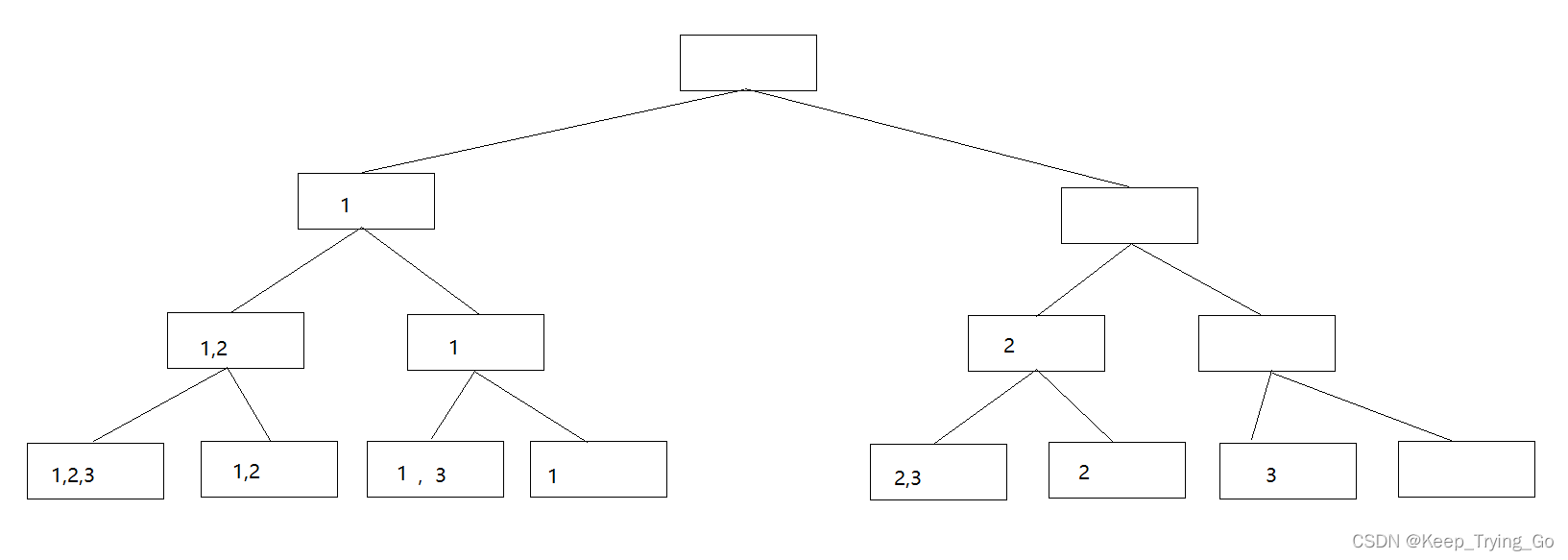
(2)求解集合的幂集
提示:求解ρ(A)集合的过程可以看成是依次对集合A中元素进行“取”或者“舍(弃)”的过程,通过上面也可以看到是一棵二叉树来表示幂集元素的状态变化状况。

- 过程:
- 树中的根节点表示幂集元素的初始状态(为空集);
- 叶子节点表示它的终结状态中幂集ρ(A)的8个元素;
- 第i层(i=1,2,3,...,n)层的分支节点,则表示已对集合A中前i-1个元素进行了取/舍处理的当前状态(其中左分支表示“取”,右分支表示“舍”);
- 将上述问题求解集合的幂集转换为先序遍历这棵状态树的过程。
(3)算法描述
void Powerset(int i,int n){
//初始调用:Powerset(1,n)
if(i>n){
输出幂集的其中一个元素
}else{
取第i个元素
Powerset(i+1,n);
舍第i个元素
Powerset(i+1,n);
}
} 提示:上述的关键问题是怎么表示“取”和“舍”的过程。
疑问:为什么说求幂集元素的过程是先序遍历状态树的过程呢?
解释:首先要清楚先序遍历的过程是先根后左再右,这样的一个遍历过程;那么在该代码中怎么体现这个先序遍历的过程的呢?从上面画出的集合的幂集二叉树图,可以看到,其实就是通过“取”或者“舍”这个方法来实现的,代码中的auxset[i-1]=set[i-1]就是在进入“左子树”的过程,也就是“取”的过程;而auxset[i-1]=0,则是在进入“右子树”的过程,也就是在“舍”的过程。如果读者还是感觉有点抽象,可以在纸上模拟一下这个过程就能深有体会了。
(4)算法实现
#include<stdio.h>
#include<string.h>
#include<stdlib.h>
#define maxn 10
//使用数组set表示集合
int set[maxn];
//使用辅助数组auxset表示取和舍的过程
int auxset[maxn];
void init(int n){
for(int i=0;i<n;i++){
set[i]=0;
auxset[i]=0;
}
}
void Powerset(int i,int n){
if(i>n){
for(int j=0;j<i-1;j++){
printf("%d ",auxset[j]);
}
printf("\n");
}else{
auxset[i-1]=set[i-1];
Powerset(i+1,n);
auxset[i-1]=0;
Powerset(i+1,n);
}
}
int main(){
int n;
printf("请输入集合的元素个数: ");
scanf("%d",&n);
init(n);
printf("请输入元素: ");
for(int i=0;i<n;i++){
scanf("%d",&set[i]);
}
Powerset(1,n);
return 0;
}
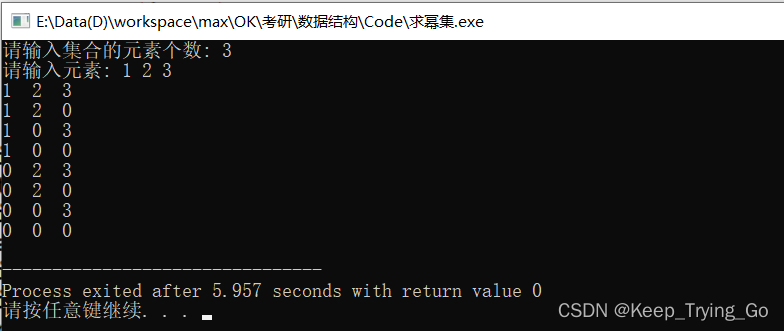
提示:我这里输出0的原因主要是因为更能表达空集。
(5)算法拓展
- 假设以线性表表示集合,则求解后的算法如下所示
实现一个顺序存储的线性表
使用C语言实现单链表的功能(带头节点)
使用C语言实现动态顺序表
使用C语言实现静态顺序表
void GetPowerset(int i,List A,List B){
//线性表A表示集合,线性表B表示幂集ρ(A)的一个元素
//局部变量K为进入函数时B的当前长度,第一次调用本函数时,B为空表,i=1
if(i>ListLength(A)){
Output(B);
}else{
GetElem(A,i,x);
int k=ListLength(B);
ListInsert(B,k+1,x);
GetPowerset(i+1,A,B);
ListDelete(B,k+1,x);
GetPowerset(i+1,A,B);
}
}参考书籍《数据结构》严蔚敏