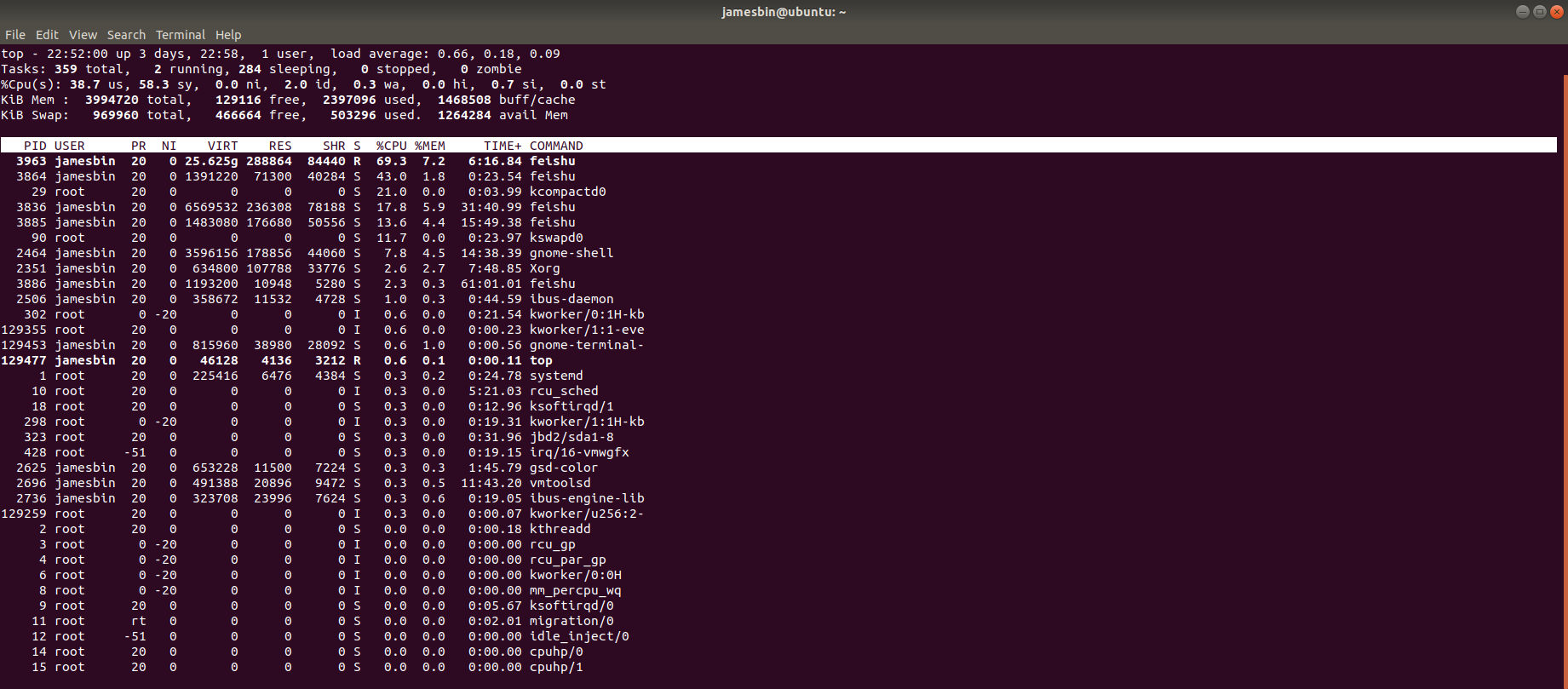
K-Means和轮廓系数

K-means（K均值）是机器学习中一种常见的无监督算法，它能够将未知标签的数据，根据它们的特征分成不同组，每一组数据又称为“簇”，每一簇的中心点称为“质心”。其基本原理过程如下：
1、任意选择K个初始质心（可以不是样本点），为每个样本点找到与其距离最近的质心，并将样本点与质心归为同一簇，从而生成K个簇；
2、当所有样本点都被分完，对于每一个簇，重新计算新的质心（同一簇中所有点的平均坐标值）；
3、不断迭代，直到不会质心的位置不发生改变。
因此该算法最核心的参数是K，那么K该如何确定呢？
这里可以引入轮廓系数S：
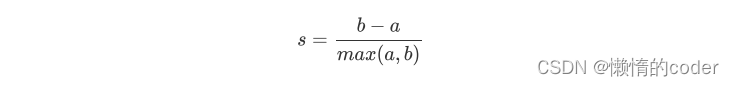
在这里插入图片描述
计算公式如上图所示，其中，a表示样本点与同一簇中所有其他点的平均距离，即样本点与同一簇中其他点的相似度；b表示样本点与下一个最近簇中所有点的平均距离，即样本点与下一个最近簇中其他点的相似度。
K-Means追求的是对于每个簇而言，其簇内差异小，而簇外差异大，轮廓系数S正是描述簇内外差异的关键指标。由公式可知，S取值范围为（-1, 1），当S越接近于1，则聚类效果越好，越接近-1，聚类效果越差。

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

#make_blobs函数是为聚类产生数据集，n_samples表示样本个数，n_features：表示数据的维度，默认为2
#centers：产生数据的中心点，默认值为3，cluster_std为数据集的标准差，浮点数或者浮点数列，默认值为1.0
x, y = make_blobs(n_samples=500,n_features=2,centers=4,random_state=1)

# 绘图，查看数据样本的分布
fig, ax = plt.subplots(1)
fig.set_size_inches(8,6)
ax.scatter(x[:, 0], x[:, 1], marker='o', s=8)
plt.show()

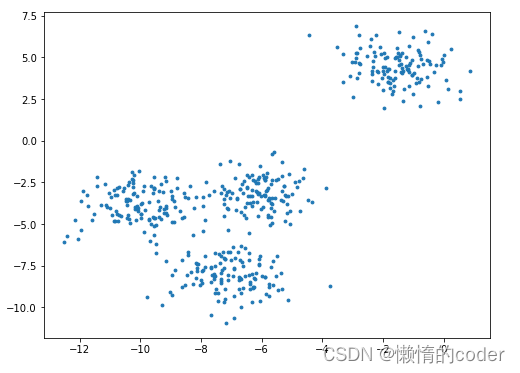
在这里插入图片描述
数据集一共由两列特征组成，即横轴和纵轴。实际应用中，数据往往会有许多列特征，一般需要先通过降维算法（如PCA）将多维特征压缩至二维或者三维，才能可视化。观察上图，乍一看，数据应该能被分成4簇，但有的人觉得分成2簇（左下1簇，右上1簇），或者分成3簇（最下面1簇，中间1簇，右上1簇）也是合理的。

那么到底能分成几类呢？这时就需要通过轮廓系数来帮我们确定。

# 给定K值（n_clusters）的范围
n_clusters = range(2, 5)

# 循环绘图
for n in n_clusters:
    # 创建绘图区域
    fig, ax = plt.subplots(1)
    fig.set_size_inches(8, 6)
    
    # 实例化
    cluster = KMeans(n_clusters=n,random_state=10).fit(x)
    # 访问labels_属性，获得聚类结果
    y_pred = cluster.labels_
    # 访问cluster_centers_属性，获得质心坐标
    centroid = cluster.cluster_centers_
    # 计算平均轮廓系数
    silhouette_avg = silhouette_score(x, y_pred)
    
    # 绘制聚类结果
    # y_pred==i会返回布尔数组，从而获得那些被分为同一类的点
    for i in range(n):
        ax.scatter(x[y_pred==i, 0],x[y_pred==i, 1],marker='o',s=8,alpha=0.7)   
    # 绘制质心
    ax.scatter(centroid[:, 0],centroid[:, 1],marker='x',s=30,c='k')   
    # 设置图表标题
    ax.set_title('result of KMeans(n_clusters={})'.format(n))   
    # 设置x轴标题
    ax.set_xlabel('feature_1')    
    # 设置y轴标题
    ax.set_ylabel('feature_2')   
    # 设置总标题，用来描述轮廓系数的值
    plt.suptitle('The average silhouette value is {:.4f}.'.format(silhouette_avg),
                 fontsize=14, fontweight='bold')
    plt.show()

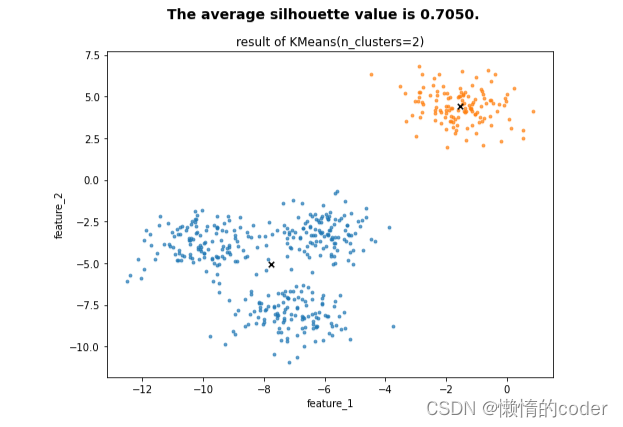
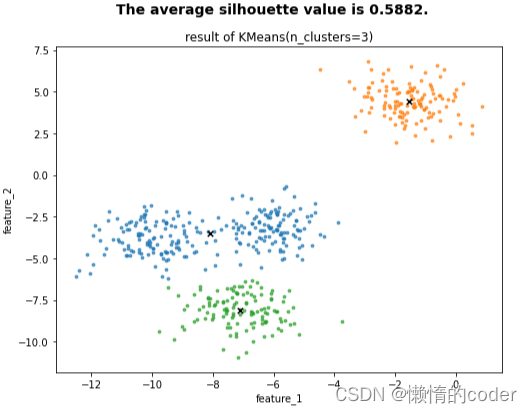
在这里插入图片描述

执行代码后，系统帮我们自动生成了3张图，并告诉我们每张图中，K的取值和平均轮廓系数值。可以看到K=2时，S=0.7050；K=3，S=0.5882；K=4，S=0.6505。当数据集被分为4簇时，轮廓系数比为3簇的高，因此我们舍弃K=3。然而当K=2时，得分竟然是最高的，这与我们最初创建数据集时给的真实分类centers=4是不一致的！
这恰恰说明了：