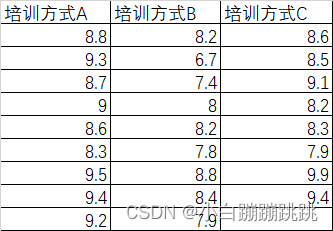
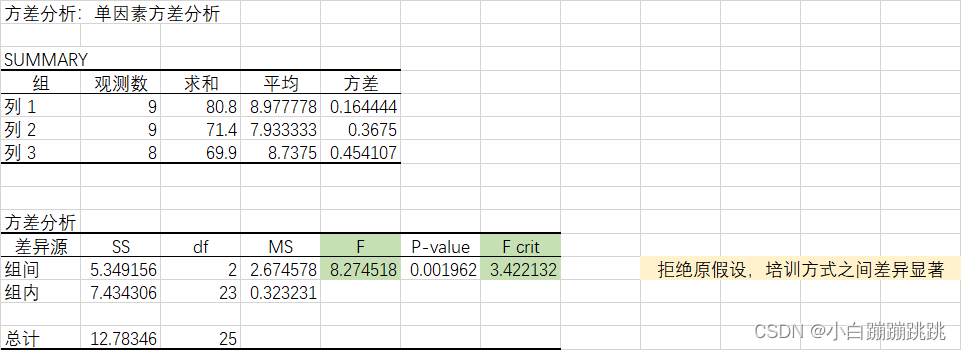
要确定不同培训方式对产品组装时间是否有显著影响，我们可以使用单因素方差分析（One-way ANOVA）。我们将使用以下数据：

培训方式 A 的样本数据
培训方式 B 的样本数据
培训方式 C 的样本数据
显著性水平（α）：0.05
我们将检验以下零假设（H₀）：

H₀: μ₁ = μ₂ = μ₃ （三种培训方式的平均组装时间相等）

与备择假设（H₁）：

H₁: 至少有一个培训方式的平均组装时间与其他培训方式不同

使用 Python 和 SciPy 库进行单因素方差分析并计算 p 值：

import numpy as np
from scipy import stats

# 样本数据
training_A = np.array([8.8, 9.3, 8.7, 9.0, 8.6, 8.3, 9.5, 9.4, 9.2])
training_B = np.array([8.2, 6.7, 7.4, 8.0, 8.2, 7.8, 8.8, 8.4, 7.9])
training_C = np.array([8.6, 8.5, 9.1, 8.2, 8.3, 7.9, 9.9, 9.4])

# 单因素方差分析ANOVA
f_stat, p_value = stats.f_oneway(training_A, training_B, training_C)

print("-----------单因素方差分析ANOVA-----------")
print("F-statistic:", f_stat)
print("p-value:", p_value)

alpha = 0.05
if p_value < alpha:
    print("拒绝原假设，训练方法之间存在显着差异。")
else:
    print("未能拒绝零假设，训练方法之间没有显着差异。")

F-statistic: 8.274517820625395
p-value: 0.0019624892439238087
拒绝原假设，训练方法之间存在显着差异。

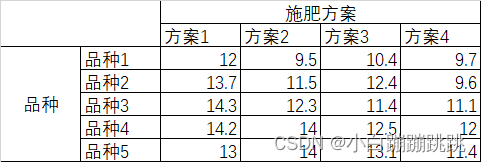
使用excel的单因素方差分析：

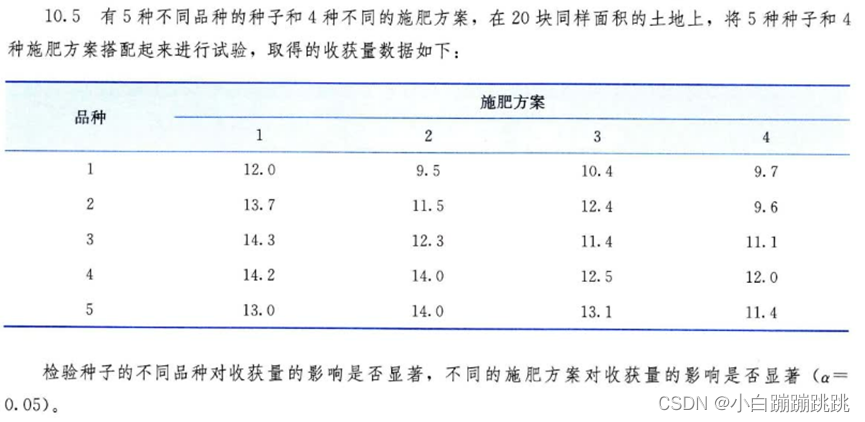
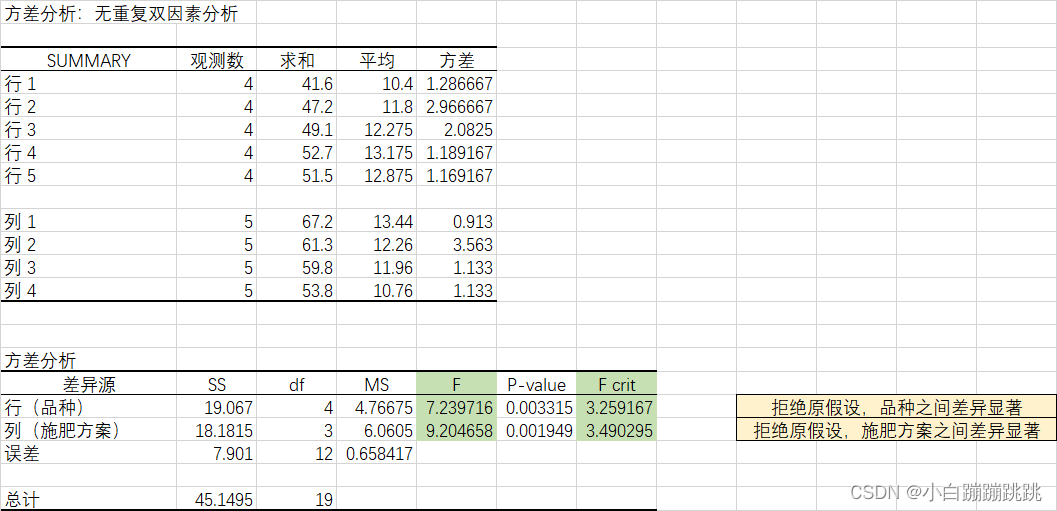
使用excel的多因素方差分析：