本文仅仅适用于已经通读过全文的小伙伴
本文代码节选自 mmdet 中的 DiffusionDet 代码,目前该代码还处于 Development 阶段,所以我博客里写的代码和之后的稳定版本可能稍有不同,不过不用担心,我们只看最关键的部分
DDPM中扩散部分有个参数 β \beta β:
q ( z t ∣ z t − 1 ) : = N ( z t ; 1 − β t z t − 1 , β t I ) q(z_t | z_{t-1}) := \mathcal{N} (z_{t}; \sqrt{1 - \beta_t} z_{t-1}, \beta_t \bf{I} ) q(zt∣zt−1):=N(zt;1−βtzt−1,βtI)
这就是每次的加噪过程,也可以视为
z
t
−
1
z_{t-1}
zt−1先经过一个缩放,再加一个随机噪声之后,就成了
z
t
z_{t}
zt。
每次加噪声通过一个参数
β
t
\beta_t
βt来控制,这个参数是人为给定的,而不是可学习的,由于:
q
(
z
t
∣
z
0
)
:
=
N
(
z
t
;
α
ˉ
t
z
0
,
(
1
−
α
ˉ
t
)
I
)
q(z_t | z_{0}) := \mathcal{N} (z_{t}; \sqrt{ \bar{\alpha}_t } z_{0}, (1-\bar{\alpha}_t) \bf{I} )
q(zt∣z0):=N(zt;αˉtz0,(1−αˉt)I)
即:
z t = α ˉ t z 0 + ϵ 1 − α ˉ t , w h e r e ϵ ∈ N ( 0 , I ) z_t = \sqrt{ \bar{\alpha}_t } z_{0} + \epsilon \sqrt{1 - \bar{\alpha}_t}, \ \ where \ \ \epsilon \in \mathcal{N}(0, \bf{I}) zt=αˉtz0+ϵ1−αˉt, where ϵ∈N(0,I)
在给定 z 0 z_{0} z0 的基础上, q ( z t ∣ z 0 ) q(z_t | z_{0}) q(zt∣z0) 也是一个高斯分布,其中:
α t = 1 − β t α ˉ t = Π s = 0 t α s \alpha_t = 1 - \beta_t \\ \bar{\alpha}_t = \Pi_{s=0}^t \alpha_s αt=1−βtαˉt=Πs=0tαs
当 α ˉ t \bar{\alpha}_t αˉt 取值趋近于0时, z t z_t zt 可以视为一个标准的高斯分布,在DiffusionDet中, β 1 : T \beta_{1:T} β1:T取了一系列零到一,且逐渐变大的值,以下是生成 β \beta β 的代码,这里我们取 T = 1000 T=1000 T=1000,即共采样 1000 1000 1000 步
def cosine_beta_schedule(timesteps, s=0.008):
"""Cosine schedule as proposed in
https://openreview.net/forum?id=-NEXDKk8gZ."""
steps = timesteps + 1
x = torch.linspace(0, timesteps, steps, dtype=torch.float64)
alphas_cumprod = torch.cos(
((x / timesteps) + s) / (1 + s) * math.pi * 0.5)**2
alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
return torch.clip(betas, 0, 0.999)
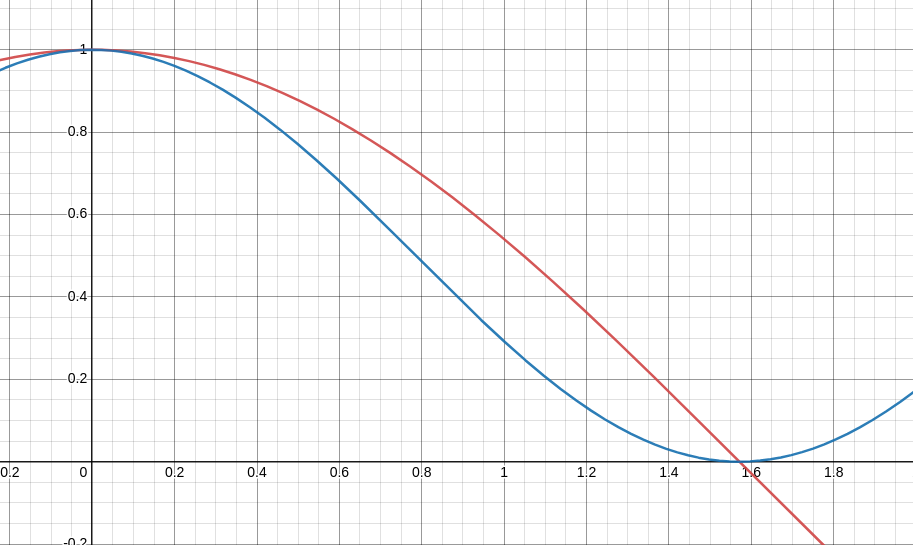
c o s ( x ) cos(x) cos(x)和 c o s 2 ( x ) cos^2(x) cos2(x) 两个函数的曲线,红线是前者,蓝线是后者,二者有同一个零点 ( π 2 , 0 ) (\frac{\pi}{2}, 0) (2π,0)
这是 β \beta β的曲线
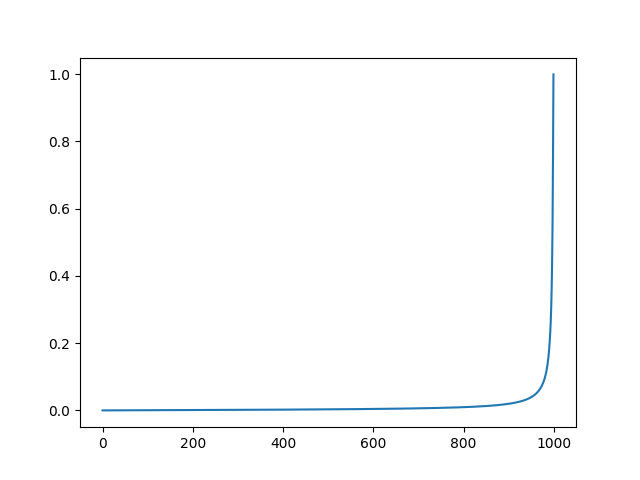
接下来就是上边计算 α \alpha α和 α ˉ \bar{\alpha} αˉ之类的代码:
def _build_diffusion(self):
betas = cosine_beta_schedule(self.timesteps)
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, dim=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.)
self.register_buffer('betas', betas)
self.register_buffer('alphas_cumprod', alphas_cumprod)
self.register_buffer('alphas_cumprod_prev', alphas_cumprod_prev)
# calculations for diffusion q(x_t | x_{t-1}) and others
self.register_buffer('sqrt_alphas_cumprod', torch.sqrt(alphas_cumprod))
self.register_buffer('sqrt_one_minus_alphas_cumprod',
torch.sqrt(1. - alphas_cumprod))
self.register_buffer('log_one_minus_alphas_cumprod',
torch.log(1. - alphas_cumprod))
self.register_buffer('sqrt_recip_alphas_cumprod',
torch.sqrt(1. / alphas_cumprod))
self.register_buffer('sqrt_recipm1_alphas_cumprod',
torch.sqrt(1. / alphas_cumprod - 1))
# calculations for posterior q(x_{t-1} | x_t, x_0)
# equal to 1. / (1. / (1. - alpha_cumprod_tm1) + alpha_t / beta_t)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (
1. - alphas_cumprod)
self.register_buffer('posterior_variance', posterior_variance)
# log calculation clipped because the posterior variance is 0 at
# the beginning of the diffusion chain
self.register_buffer('posterior_log_variance_clipped',
torch.log(posterior_variance.clamp(min=1e-20)))
self.register_buffer(
'posterior_mean_coef1',
betas * torch.sqrt(alphas_cumprod_prev) / (1. - alphas_cumprod))
self.register_buffer('posterior_mean_coef2',
(1. - alphas_cumprod_prev) * torch.sqrt(alphas) /
(1. - alphas_cumprod))
这三行计算了 β t \beta_t βt, α ˉ t \bar{\alpha}_t αˉt 和 α ˉ t − 1 \bar{\alpha}_{t-1} αˉt−1,其长度都是 T T T
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, dim=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.)
self.register_buffer('betas', betas)
self.register_buffer('alphas_cumprod', alphas_cumprod)
self.register_buffer('alphas_cumprod_prev', alphas_cumprod_prev)
q ( z t ∣ z t − 1 ) : = N ( z t ; 1 − β t z t − 1 , β t I ) q(z_t | z_{t-1}) := \mathcal{N} (z_{t}; \sqrt{1 - \beta_t} z_{t-1}, \beta_t \bf{I} ) q(zt∣zt−1):=N(zt;1−βtzt−1,βtI)
接下来计算 α ˉ t \sqrt{\bar{\alpha}_{t}} αˉt, 1 − α ˉ t \sqrt{1 - \bar{\alpha}_{t}} 1−αˉt, log ( 1 − α ˉ t ) \log{(1-\bar{\alpha}_{t})} log(1−αˉt), 1 α ˉ t \frac{1}{\sqrt{\bar{\alpha}_{t}}} αˉt1和 1 α ˉ t − 1 \sqrt{\frac{1}{\bar{\alpha}_t} - 1} αˉt1−1
# calculations for diffusion q(x_t | x_{t-1}) and others
self.register_buffer('sqrt_alphas_cumprod', torch.sqrt(alphas_cumprod))
self.register_buffer('sqrt_one_minus_alphas_cumprod',
torch.sqrt(1. - alphas_cumprod))
self.register_buffer('log_one_minus_alphas_cumprod',
torch.log(1. - alphas_cumprod))
self.register_buffer('sqrt_recip_alphas_cumprod',
torch.sqrt(1. / alphas_cumprod))
self.register_buffer('sqrt_recipm1_alphas_cumprod',
torch.sqrt(1. / alphas_cumprod - 1))
DDPM文中假设,后验分布 q ( z t − 1 ∣ z t , z 0 ) q(z_{t-1} | z_t, z_0) q(zt−1∣zt,z0)也是高斯分布,有:
q ( z t − 1 ∣ z t , z 0 ) = N ( z t − 1 ; μ ~ ( z t , z 0 ) , β t ~ I ) q(z_{t-1} | z_t, z_0) = \mathcal{N} (z_{t-1} ; \tilde{\mu}(z_t, z_0), \tilde{\beta_t} \bm{I}) q(zt−1∣zt,z0)=N(zt−1;μ~(zt,z0),βt~I)
算式整理后有:
μ ~ t ( z t , z 0 ) = α ˉ t − 1 β t 1 − α ˉ t z 0 + α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t z t \tilde{\mu}_t(z_t, z_0) = \frac{ \sqrt{\bar{\alpha}_{t-1}} \beta_t }{ 1 - \bar{\alpha}_t } z_{0} + \frac { \sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1}) } { 1 - \bar{\alpha}_t } z_{t} μ~t(zt,z0)=1−αˉtαˉt−1βtz0+1−αˉtαt(1−αˉt−1)zt
β ~ t = 1 − α ˉ t − 1 1 − α ˉ t β t \tilde{\beta}_{t} = \frac { 1 - \bar{\alpha}_{t-1} } { 1 - \bar{\alpha}_t } \beta_{t} β~t=1−αˉt1−αˉt−1βt
接下来的几行代码用来计算这几个系数:
# calculations for posterior q(x_{t-1} | x_t, x_0)
# equal to 1. / (1. / (1. - alpha_cumprod_tm1) + alpha_t / beta_t)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (
1. - alphas_cumprod)
self.register_buffer('posterior_variance', posterior_variance)
# log calculation clipped because the posterior variance is 0 at
# the beginning of the diffusion chain
self.register_buffer('posterior_log_variance_clipped',
torch.log(posterior_variance.clamp(min=1e-20)))
self.register_buffer(
'posterior_mean_coef1',
betas * torch.sqrt(alphas_cumprod_prev) / (1. - alphas_cumprod))
self.register_buffer('posterior_mean_coef2',
(1. - alphas_cumprod_prev) * torch.sqrt(alphas) /
(1. - alphas_cumprod))
以上就是函数 _build_diffusion 的全部内容,集中几个log项可能是之后计算loss用的