从x的n次方看递归时间复杂度计算

1.循环

这个问题，最简单的办法是用循环

int pow1(int x,int n)
{
	int result = 1;
    for(int i=0;i<n;i++)
    {
        result*=x;
    }
    return result;
}

如上算法的时间复杂度为O(N)，但还是不够理想。这时尝试使用递归算法

2.递归1

int pow2(int x,int n)
{
	if(n==0)// x^0 = 1
        return 1;
    return pow2(x,n-1)*x;
}

使用如上递归函数时间复杂度计算办法，该函数递归调用次数是从n一直减到0，即n次。每次递归中，需要进行一次相乘的计算，即O(1)

最终得到的时间复杂度 O(n*1) = O(n)，这和我们用循环写出来的代码没两样

3.递归2，二叉树

int pow3(int x,int n)
{
	if(n==0)// x^0 = 1
        return 1;
    if(n==1)// 减少一次递归
        return x;
    if(n%2==1)// 奇数
    	return pow3(x,n/2)*pow3(x,n/2)*x;
    // 偶数方
    return pow3(x,n/2)*pow3(x,n/2);
}

最终求次方操作被抽象成了一个二叉树

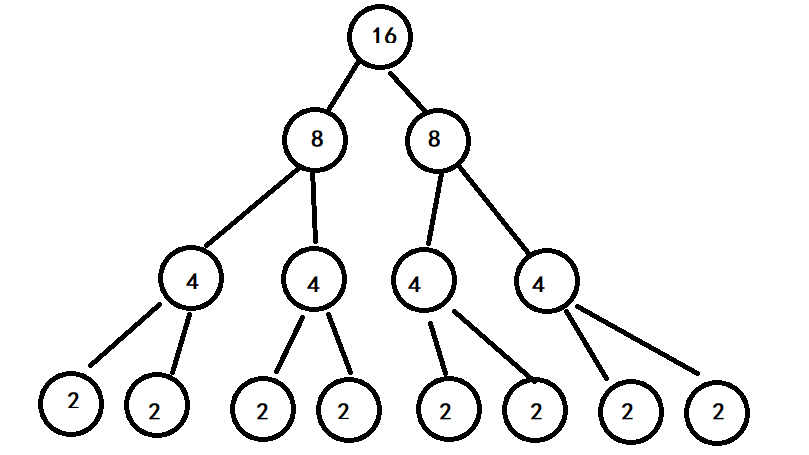
总递归次数，即二叉树中的节点个数。我们能算出来这颗满二叉树的节点个数为 2^4-1 = 15

所以一共递归了15次，每次的操作还是一个相乘，O(1)

所以最终的时间复杂度就是

递归次数 = 满二叉树节点个数 = 2^m -1
m = 二叉树层数（从1开始）= log(n)

带入可以计算出来，最终的二叉树总节点数是n-1个，时间复杂度还是O(N)。这说明我们的算法还不够好

二叉树相关知识点 https://blog.musnow.top/posts/4161984418/

4.递归3

如果观察第三个函数可以发现，不管是奇数还是偶数的奇怪，都进行了2次递归调用，但这两个递归调用都是完全相同的

pow3(x,n/2)*pow3(x,n/2);

也就是说，我们可以先递归调用1次，存结果再计算！

int pow4(int x,int n)
{
	if(n==0)// x^0 = 1
        return 1;
    if(n==1)// 减少一次递归
        return x;
    int tmp = pow3(x,n/2);
    if(n%2==1)// 奇数
    	return tmp*tmp*x;
    // 偶数方
    return tmp*tmp;
}

此时函数中只调用了1次递归，每次递归之后，数据都除2，所以总共是log₂(n)次

每次递归，还是一个乘法操作，时间复杂度O(1)
$$O(1\ast lo{g}_{2}n)$$
最终得到的时间复杂度就是O(logN)！

The end

这才是我们需要的时间复杂度较低的算法，同时也复习了递归调用的时间复杂度计算办法

递归时间复杂度 = 递归次数 * 每次操作的负载度