416. 分割等和子集（中等）

在这里插入图片描述

方法一： 0-1背包问题的普通解法

思路
- 首先，对题目做一个等价转换：「是否可以从数组中选择一些正整数，使这些数的和等于整个数组元素和的一半」。
- 这样就可以看作一个 0-1背包问题，它的特点是：每个数只能用一次。解决的基本思路是：物品一个个选，容量也一点一点增加去考虑。
- 具体的做法是：画一个 n * (mid+1) 的表格，其中 n 是物品的个数， mid 是背包的容量。n 行表示一个个物品考虑， mid+1 多出来的那一列，表示容量从 0 开始考虑。
- 状态定义：dp[i][j] 表示从数组的 [0，i] 这个子区间内挑选一些正整数，每个数只能用一次，使这些数的和恰好等于 j。
- 状态转移方程：很多时候，状态转移方程的思考角度是 分类讨论 ，对于 0-1 背包问题就是「考虑当前的数字选或者不选」。
  - 不选择 nums[i] ，如果在 [0， i-1] 这个子区间内已经有一部分元素，使得它们的和为 j ，那么 dp[i][j] = true；
  - 选择 nums[i] ，如果在 [0，i] 这个子区间内就得找到一部分元素，使得它们的和为 j-nums[i]。
- 初始化条件：
  - j-nums[i] 作为数组下标，需要保证大于等于 0，因此 nums[i] <= j ；
  - 当 j == nums[i] 的时候，一定能够保证 dp[i][j] = true;
- 完整的状态转移方程：

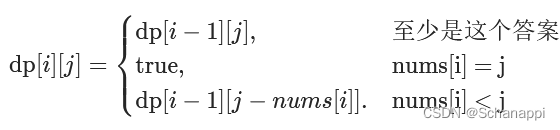
代码

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        int sum = accumulate(nums.begin(), nums.end(), 0);
        // 特判：如果sum为奇数 则不符合要求
        if(sum % 2) return false;
        int mid = sum / 2;
        // dp[0][0] = false : 因为数组中不含0 因此元素和不可能为0
        vector<vector<bool>> dp(n, vector<bool>(mid + 1, false));
        // 先填表格的第0行，第一个数只能让容积为它自己的背包装满
        if(nums[0] <= mid){
            dp[0][nums[0]] = true;
        }
        for(int i=1; i<n; ++i){
            for(int j=0; j<=mid; ++j){
                // 直接把上一行的结果抄下来，之后再修正
                dp[i][j] = dp[i-1][j];
                if(j > nums[i]){
                    dp[i][j] = dp[i-1][j - nums[i]] || dp[i-1][j];
                }
                else if(j == nums[i]){
                    dp[i][j] = true;
                    continue;
                }
            }
        }
        return dp[n-1][mid];
    }
};

收获
- 这道题看起来不难，但是思考了很久，感觉自己还是没掌握背包问题。

解法二：空间压缩

思路
- 「0-1背包问题」常规优化：「状态数组」从二维降到一维，减少空间复杂度。
- 在「填表格」的时候，当前行总是参考了它上面一行「头顶上」那个位置和「左上角」某个位置的值。因此，可以只开一个一维数组，从后向前依次填表即可。
- 「从后向前」写的过程中，一旦nums[i] <=j 不满足，可以马上退出当前循环，因为后面的j的值肯定越来越小，没有必要继续做判断，直接进入外层循环的下一层。相当于也是一个剪枝，这一点是「从前向后」填表所不具备的。

代码

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int n = nums.size();
        int sum = accumulate(nums.begin(), nums.end(), 0);
        // 特判：如果sum为奇数 则不符合要求
        if(sum % 2) return false;
        int mid = sum / 2;
        // dp[0][0] = false : 因为数组中不含0 因此元素和不可能为0
        vector<bool> dp(mid + 1, false);
        // 第一个数只能让容积为它自己的背包装满
        if(nums[0] <= mid){
            dp[nums[0]] = true;
        }
        for(int i=1; i<n; ++i){
            for(int j=mid; j>=nums[i]; --j){
                if(j == nums[i])    dp[j] = true;
                else if(j > nums[i]){
                    dp[j] = dp[j - nums[i]] || dp[j];
                }
            }
        }
        return dp[mid];
    }
};