---

1. 位图

1.1 位图的概念

💭位图（bitset）是一种基于哈希思想设计的数据结构，其功能主要用于判断数据是否已存在。适用于海量数据，且数据不重复的场景。

以一个问题引入：给40亿个不重复的无符号整数，无序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。

🔎暴力查找法：遍历所有数据，查找目标数是否存在于数据中。但是，因为数据巨大，遍历效率会很慢。
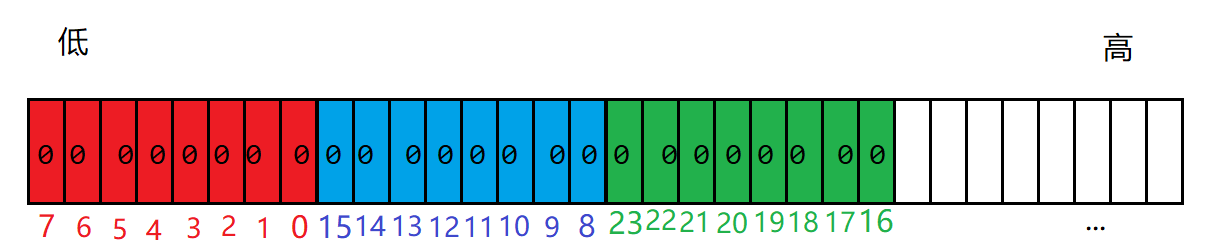
🔎二分查找法：但要先排序，排序要在内存中排，40亿个整数大约要占16G空间（推导过程如下图），内存空间不足。

因此以上两种方法都不适应，此时就要上位图了。

---

1.2 位图的结构

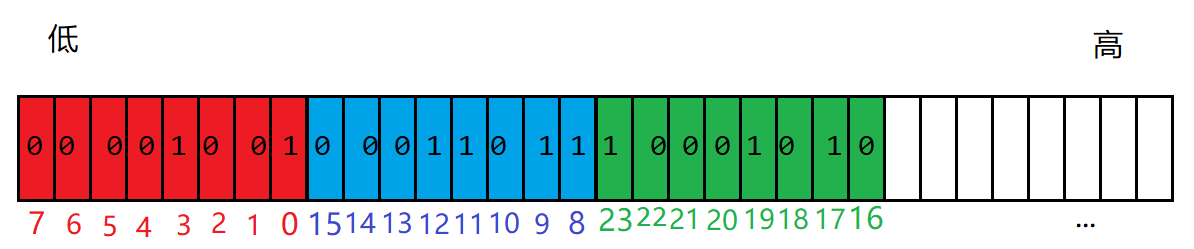
⭕位图以一个个比特位组成，每个比特位代表一种状态，且每个位都有一个下标。位图中的状态为1表示对应下标的数据存在，为0表示对应下标的数据不存在。

举个栗子：假设有如下一组数据，用位图表示

int arr = {3,11,8,23,12,9,0,19,17}; 

---

1.3 位图的实现

namespace ckf
{
	template <size_t N> // 范围 0~N
	class bitset
	{
	public:
		bitset()
		{
			_bits.resize(N / 8 + 1, 0);
		}

		// 给第x位置1
		void set(size_t x)
		{
			size_t i = x / 8;
			size_t j = x % 8;

			_bits[i] |= (1 << j);
		}
		
		// 给第x位置0
		void reset(size_t x)
		{
			size_t i = x / 8;
			size_t j = x % 8;

			_bits[i] &= ~(1 << j);
		}
		
		// 检测第x位是否存在
		bool test(size_t x)
		{
			size_t i = x / 8;
			size_t j = x % 8;

			return _bits[i] & (1 << j);
		}

	private:
		vector<char> _bits;
	};
}

---

2. 布隆过滤器

2.1 概念

💭位图只能应用于整数，如果想存储其他类型应该怎么办呢？用布隆过滤器。

布隆过滤器（Bloom Filter）是一种快速、高效的数据结构，用于检测一个元素是否属于某个集合。它通过使用一个位数组和多个哈希函数来判断一个元素是否可能在集合中。

布隆过滤器的主要应用是在大规模数据集合中判断某个元素是否存在，比如网络爬虫中URL的去重、大型分布式系统中的缓存机制等。布隆过滤器可以节省存储空间，因为它不需要将元素本身存储在数据结构中，只需要存储其哈希值。

但是，布隆过滤器也存在一些缺点，如误判率高和无法删除元素等。在使用时需要根据具体场景进行权衡和选择。

2.2 结构

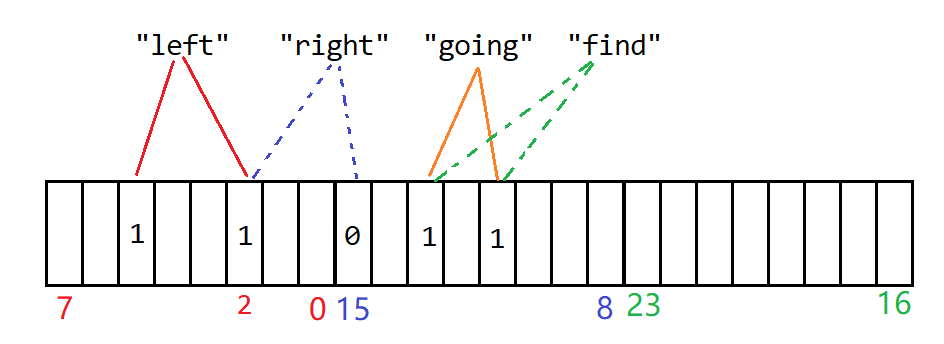
⭕假设向布隆过滤器插入了"left"、"going"三个字符串，分别通过两个哈希函数映射到位图数组上。而"right","find"此时并不在布隆过滤器中，但是由于哈希函数映射与已在的字符串相同，导致它们在位图上的比特位存在1，这就是布隆过滤器的误判。

得出结论：布隆过滤器中，元素通过哈希函数映射后，若每个位都为1，则不一定存在（可能误判），若存在一个位为0，则该元素一定不存在。因此布隆过滤器只能判断元素不存在，因此起到了过滤的作用。

• 如何选择哈希函数个数和布隆过滤器长度
  参考文章：详解布隆过滤器的原理，使用场景和注意事项

---

2.3 布隆过滤器的实现

// N为最多能插入的数据个数
template <size_t N, size_t X = 5,class K = string, 
	class HashFunc1 = BKDRHash<K>, 
	class HashFunc2 = SDBMHash<K>, 
	class HashFunc3 = RSHash<K>>
class bloom_filter
{
public:
	void set(const K& key)
	{
		size_t len = N * X;

		size_t hash1 = HashFunc1()(key) % len;
		size_t hash2 = HashFunc2()(key) % len;
		size_t hash3 = HashFunc3()(key) % len;

		_bs.set(hash1);
		_bs.set(hash2);
		_bs.set(hash3);
	}

	bool test(const K& key)
	{
		size_t len = N * X;

		size_t hash1 = HashFunc1()(key) % len;
		if (!_bs.test(hash1))
		{
			return false;
		}

		size_t hash2 = HashFunc2()(key) % len;
		if (!_bs.test(hash2))
		{
			return false;
		}

		size_t hash3 = HashFunc3()(key) % len;
		if (!_bs.test(hash3))
		{
			return false;
		}

		return true;
	}

private:
	bitset<N* X> _bs;
};