二分查找一般运用在有序数组中的查找,一般分为开区间、闭区间和半开半闭区间三种写法
闭区间
闭区间是指包含左右两边元素的区间,例如:区间[a, b]包含元素 a b ,称为闭区间。
代码1
# 左闭右闭 区间写法 在数组 nums 中寻找 target
def left_close_right_close(nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
# 闭区间 [left, right]
while left < right:
mid = (left + right) // 2
if nums[mid] < target:
# 更新闭区间 [mid+1, right]
left = mid + 1
else:
# [left, mid-1]
right = mid - 1
print('left is {} ans num is {}, right is {} and nums is {}'.format(left, nums[left], right, nums[right]))
return left
开区间
开区间是指不包含左右两边元素的区间,例如:区间(a, b)不包含元素 a b,称为闭区间
代码2
# 左开右开区间写法
def left_open_right_open(nums: List[int], target: int) -> int:
# 左开区间,所以 是 -1
left = -1
# 因为是右开区间
right = len(nums)
# 左开右开区间 [left, right)
while left + 1 < right:
mid = (left + right) // 2
print("mid is {}".format(mid))
if nums[mid] < target:
# 更新左开区间 (mid, right)
left = mid
else:
# 更新右开区间 (left, mid)
right = mid
print('left index is {}, right index is {}'.format(left, right))
return right
半开半闭区间
除了闭区间和开区间以外还有半开半闭区间
搞清楚有了几种区间写法之外,接下来举例说明。
分类讨论
- 在有序不重复数组寻找目标元素
- 在有序含有重复元素数组中寻找目标元素
不含重复元素
左闭右闭区间
- 示例数据:
arr = [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14]- 寻找数组位于非边缘位置的元素,以寻找元素 12 为例
- 由 “代码1” 可知,最终返回的数组下标为
left - 运行结果如下
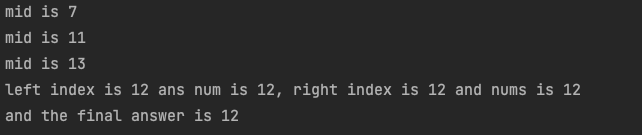
- 图示说明,为什么最终返回
left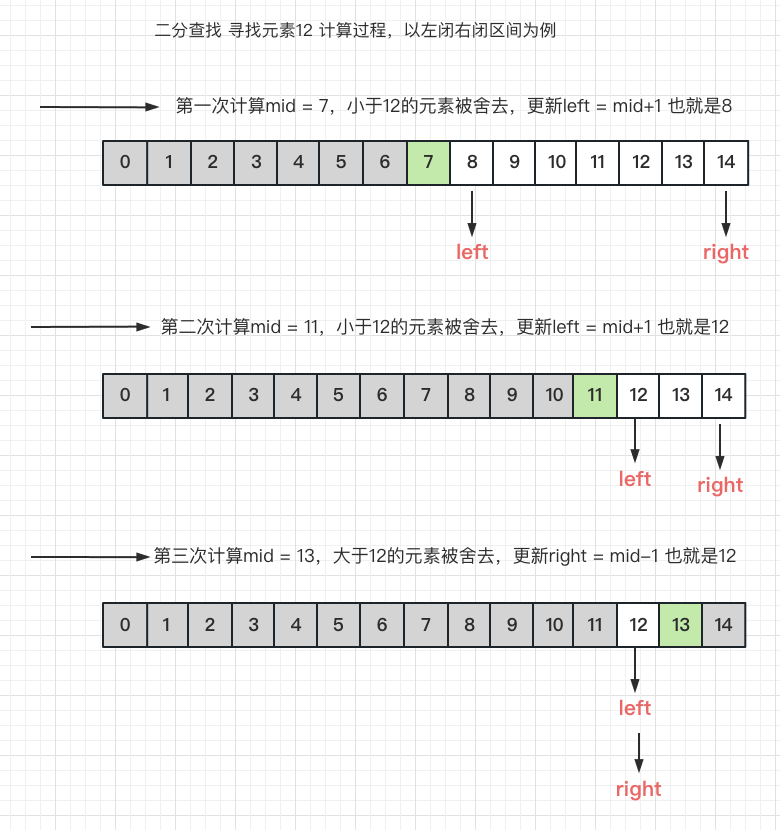
- 由上图可知查找最终的目标元素,当找到的时候需要返回left,如果判断条件是
left < right那么返回right也是同样的
- 代码详尽注释版
# 二分查找左闭右闭区间
def left_close_right_close(nums: List[int], target: int) -> int:
# 因为是左闭合区间,所以左边的开始起点为 left = 0 因为 0 是数组的第一个下标位置
# 如果是左开区间,那么初始化左边起点为 -1
left = 0
# 同理,初始化右边起点为 right = len(nums) - 1
# 如果是 右开区间,那么 right 起点为 len(nums)
right = len(nums)
# 这里如果是 小于等于 的话,最终 left = right + 1 将会重合 (target在数组中存在的情况下)
while left < right:
mid = (left + right) // 2
if nums[mid] > target:
# 更新区间 [left, right = mid - 1]
right = mid - 1
else:
# 更新区间 [left = mid + 1, right]
left = mid + 1
# return left or right 因为 判断条件是 left < right 所以 最终跳出循环 left = right
return left
- 如果要查找的元素在数组中不存在
- **如果查找的元素大于数组中的最大值,结果返回 **
**left = 数组长度** - 如果查找的元素小于数组中的最小值,结果返回
**left = 0** - 总结:左闭右闭区间适用于查找目标元素不在数组边界的元素,这一点要注意
- **如果查找的元素大于数组中的最大值,结果返回 **
左开右开区间
- 直接上代码
# 左开右开区间写法
def left_open_right_open(nums: List[int], target: int) -> int:
# 左开区间,所以 是 -1
left = -1
# 因为是右开区间
right = len(nums)
# 左开右开区间 [left, right)
while left + 1 < right:
mid = (left + right) // 2
print("mid is {}".format(mid))
if nums[mid] < target:
# 更新左开区间 (mid, right)
left = mid
else:
# 更新右开区间 (left, mid)
right = mid
print('left index is {}, right index is {}'.format(left, right))
return right
- 与左闭右闭写法的区别
- 首先是判断条件
left+1 < right那么最终返回的时候left+1 = right - 更新区间不用再进行加减,直接更新 left 或者 right 即可
- 最终返回的元素结果是
right因为判断条件是left + 1 < right - 如果查找的元素不存在,最终
right = 数组长度+1orright = 0 - 需要特别注意的是,查找数组的第一个元素和小于数组中最小值的元素,返回结果相同
- 需要特别注意的是,查找数组的第一个元素和小于数组中最小值的元素,返回结果相同
- 需要特别注意的是,查找数组的第一个元素和小于数组中最小值的元素,返回结果相同
- 首先是判断条件
左开右闭区间
- 直接上代码
# 左开右闭 区间写法
def left_open_right_close(nums: List[int], target: int) -> int:
left = -1
# 因为是右闭区间
right = len(nums) - 1
# 左开右闭 (left, right]
while left < right:
# mid = (left + right + 1) // 2
mid = left + (right + 1 - left) // 2
print("mid is {}".format(mid))
if nums[mid] < target:
# 更新开区间 (mid, right)
left = mid
else:
# 更新闭区间 (left, mid - 1]
right = mid - 1
print('left index is {}, right index is {}'.format(left, right))
return right + 1
- 寻找不同点
- 左开右闭 初始化
left = -1, right = len(nums) - 1 - 计算mid的时候不同
mid = left + (right + 1 - left) // 2- 这里要注意上面的写法等同于
mid = (right + 1 - left) // 2 - 为什么要 进行
right + 1 - left->因为右边是闭合区间,仿照左开右开区间写法,所以进行right + 1
- 这里要注意上面的写法等同于
- 由于判断条件是
left < right,所以最终返回left = right - 最终的返回结果是
left + 1 or right + 1 - 同样的要注意查找数组中最小值的情况
- 左开右闭 初始化
左闭右开区间
- 直接上代码
# 左闭右开区间
def left_close_right_open(nums: List[int], target: int) -> int:
left = 0
right = len(nums)
while left < right:
mid = left + (right - 1 - left) // 2
print('the mid is {}'.format(mid))
if nums[mid] > target:
# 右开区间,直接更新右开区间
right = mid
else:
# 左闭区间,更新左区间 +1
left = mid + 1
print('final the left is {},the right is {}'.format(left, right))
return right - 1
- 寻找不同点
- 左闭右开 初始化
left = 0, right = len(nums) - 计算mid
mid = left + (right - 1 - left)减1计算 - 最终结果
left = right返回left - 1orright - 1 - 注意寻找边界元素的情况
- 左闭右开 初始化
含有重复元素
- 示例数据:
arr1 = [1,2,3,4,4,4,4,5] arr2 = [1,2,2,2,2,2,3,4,5] - 对于含有重复元素的情况,一般需要找到其第一次出现或最后一次出现的位置。
左开右开和左闭右闭
- 测试左开右开和左闭右闭写法的运行效果
- 左闭右闭没有找到正确元素
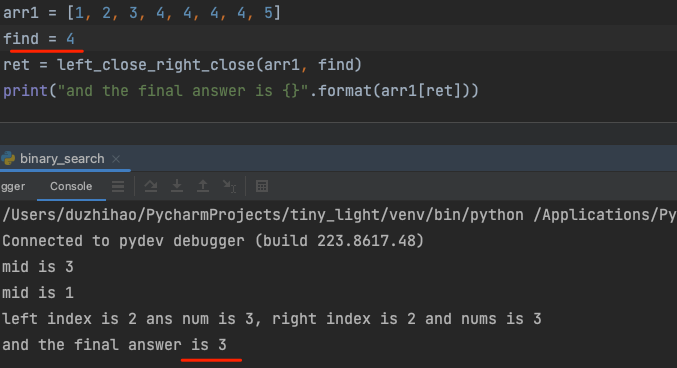
- 左开右开找到了正确元素,但是没有办法正确找到重复元素的右边界
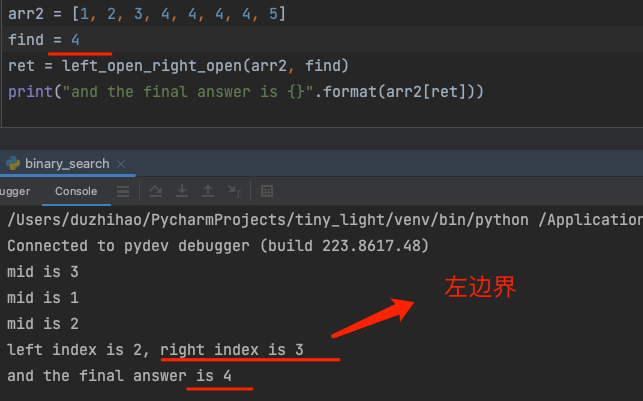
查找左边界和右边界
左开右闭查找左边界
- 测试结果直接上
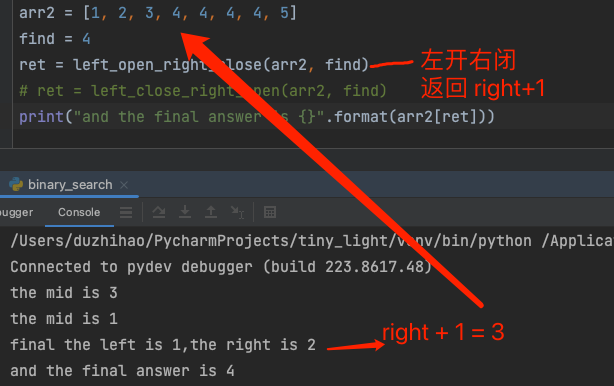
- 为什么?
- 因为左开右闭的区间查找元素最终返回结果是
right + 1向右偏移,最终求得左边界
- 因为左开右闭的区间查找元素最终返回结果是
左闭右开查找右边界
- 同理,左闭右开区间查找右边界