实验目的

通过本次实验，了解算法复杂度的分析方法，掌握递归算法时间复杂度的递推计算过程。

实验内容

二路归并排序的算法设计和复杂度分析。

实验过程

1.算法设计
归并排序：是指将两个或两个以上的的有序序列合并成一个有序序列。
排序思想：
（1）将每一个数据看成一个单独的有序序列，则n个待排序数据就是n个长度唯一的有序子序列；
（2）对所有有序子序列进行两两归并，得到n/2个长度为1或2的有序子序列–这这为一趟归并；
（3）重复（2），直到得到长度为n的有序序列为止。
上述排序过程中，子序列总是两两归并，极为二路归并排序。这算法设计的重点是如何将相邻的两个子序列归并成一个子序列。
算法实验原理：
1、申请一个和原始排序数组空间一样大的额外数组。
2、定义归并初始长度 length。
3、将数组分块。
4、将分块数组进行排序，把数据存入额外一个数组。（下一次用额外数组排序，数据存入原始数组，轮流存储）
5、增加归并长度 length*2。
6、重复3-5步，即可得到排序。
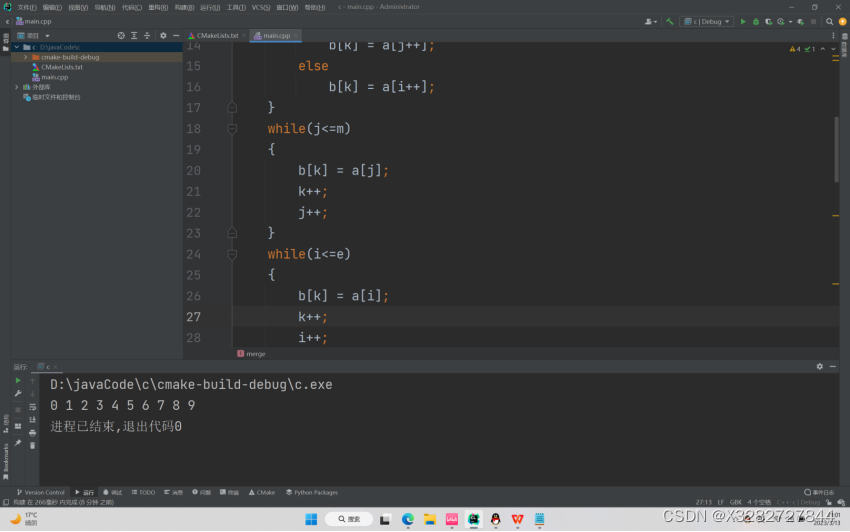
2.程序清单

#include <stdio.h>
#include <stdlib.h>
// 将a[s...m]和a[m+1...e]两个有序子序列归并为有序
// 归并后的序列存放数组b中 
void merge(int a[], int s, int m, int e)
{
    int i,j,k;
    // 申请临时空间存放有序序列
    int *b = (int *)malloc(sizeof(int)*(e-s+1));

    for(i=m+1,k=0,j=s; j<=m && i<=e; ++k)
    {
        if(a[j] <= a[i])
            b[k] = a[j++];
        else
            b[k] = a[i++];
    }
    while(j<=m)
    {
        b[k] = a[j];
        k++;
        j++;
    }
    while(i<=e)
    {
        b[k] = a[i];
        k++;
        i++;
    }
    // 排序完成后，复制到原数组a
    for(i=s,k=0; i<=e; i++,k++)
        a[i] = b[k];
    free(b);
}
// 对a[s...e]序列进行归并排序 
void msort(int a[], int s, int e)
{
    if (s<e)
    {
        // 将整个序列一分为二
        int m = (s+e)/2;
        msort(a,s,m);
        msort(a,m+1,e);
        merge(a,s,m,e);
    }
}
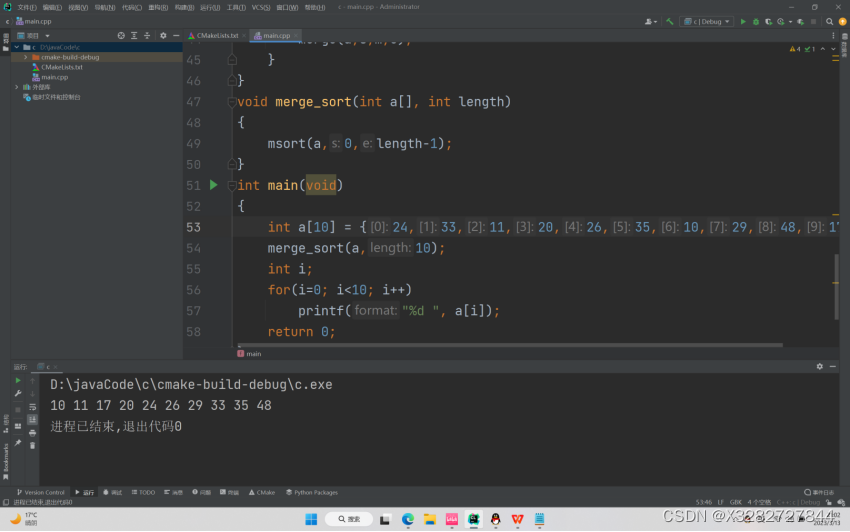
void merge_sort(int a[], int length)
{
    msort(a,0,length-1);
}
int main(void)
{
    int a[10] = {4,3,1,2,6,5,0,9,8,7};
    merge_sort(a,10);
    int i;
    for(i=0; i<10; i++)
        printf("%d ", a[i]);
    return 0;
}

运行结果

复杂度分析