π和e
1. 圆周率π
耳熟能详的π,到底是什么,怎么来的?
圆周率π,圆的周长C=2πr,其中r是圆的半径
1.1 刘徽割圆术
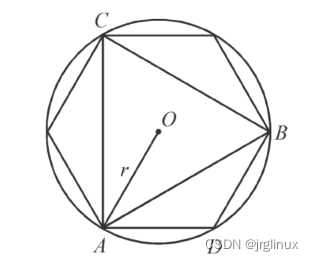
如图中所示,作出圆内的正十二边形,正二十四边形,…,用这种思想去无限逼近圆的周长。这是我国魏晋时期的数学家刘徽的割圆术思想。(是不是形同微积分?)
1.2 π的数学定义
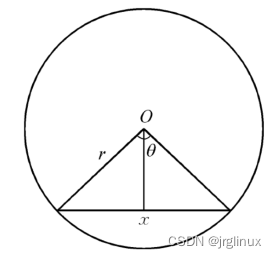
对于圆内的正n边形(n=3,4,5,…),对于上图中的θ角,有θ=360°/n,则对于该正n边形的边长x有
x=2rsin(θ/2),那么通过正n边形的周长即可近似计算圆的周长:
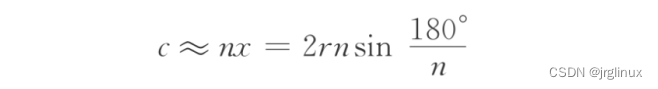
当n趋向于无穷大,nx就无限逼近与圆周长C。 用微积分的数学表述则是:
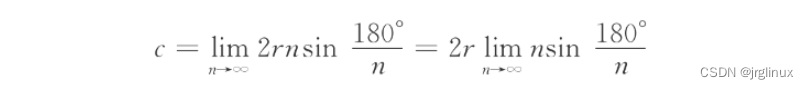
令
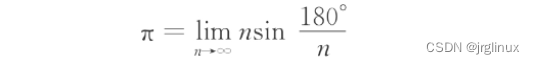
则有圆的周长:
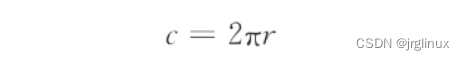
这样便得到π的数学表达式。(注意看,π的数学定义中就有sin()三角函数,大自然奇妙就奇妙在无法解释之处,不是么)
2. 自然底数e
2.1 复利公式
学过初等数学的都知道自然底数e,e=2.71828…,那么e到底怎么来的呢?
据说最初e并不是在数据界诞生的,而是为了解决金融复利问题:
-
假设在银行存款本金1元,年利率是100%(有点疯狂),一年之后本息合计多少钱?
1x(1+100%) = 2元
-
假设按月计息,月利息按100%/12算,一年之后本息是多少?
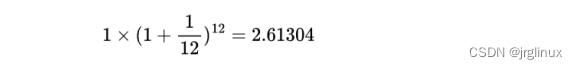
-
假设按周计息呢,周利息按1/52算,一年之后本息是多少?
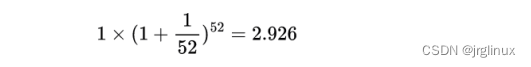
- 将一年时间划分成n份,单位时间内利息为1/n,一年之后本息是多少?考虑极限情况呢?

2.2 e的数学定义
对于上面例子中的,得出e的数学定义
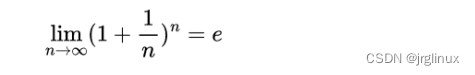
对于上述e的数学定义来说,e到底等于多少呢?是不是一个确定值呢?
这里需要用一下牛顿二项式定理:
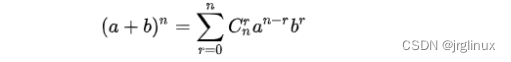
使用牛顿二项式定理对e进行展开计算:
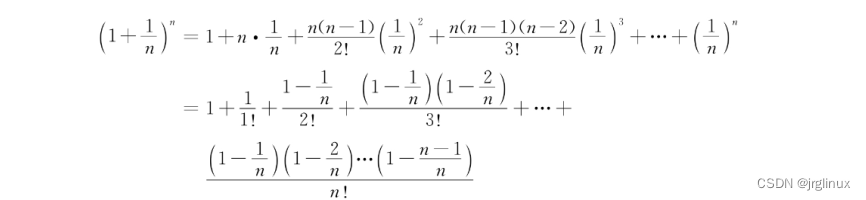
则可推导对于 n -> ∞ 时:
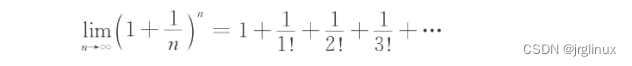
由此,可以推出e的另一个数学表达式,级数展开式:

3. 级数展开式
3.1 π的级数展开式
苏格兰数学家格雷戈里在1671年推出一个公式:
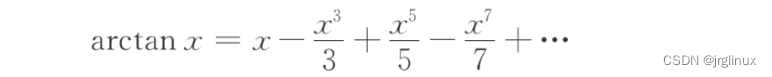
该公式的推导证明比较复杂,涉及泰勒级数、牛顿插值法等,其实它们之间都互推有关系的,而且泰勒生年还在格雷戈里之后呢,那段历史感兴趣的可以去读读,这里就不考古哪个公式到底是谁提的,只看数学公式。将格雷戈里公式中x=1,则可得到π的级数展开式:
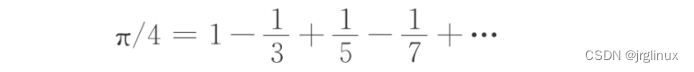
是不是终于感觉π不再神乎其乎的了,可以用完全看得懂阿拉伯数字和加减符号写出来了?就是这么神奇。
3.2 e的级数展开式
上一节中,已经提到了e的级数展开,就是:
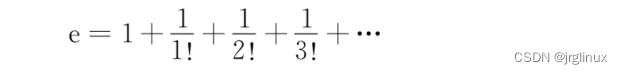
π = 3.14159…
e = 2.71828…
无理数,或称为无限不循环小数,不能写作两整数之比,若将它写成小数形式,则小数部分是无限不循环。π和e都是无理数。证明略。
超越数,超越数是不能作为有理系数多项式方程的根的数,π和e都是超越数。证明略。
4. 欧拉公式
自然底数e也叫欧拉数e,因为欧拉是最早广泛研究它的,并取名e,所以也就叫欧拉数。
公元1748年,欧拉给出了那个让世界为之闪耀的公式欧拉公式:
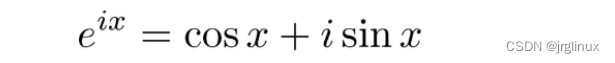
其中,e是自然底数,i是虚数单位。令x=π,则欧拉公式简化为:
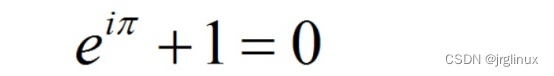
神不神奇,该公式由自然底数e,圆周率π,虚数单位i,自然数单位1,以及永恒的0组成。
看下面这个复平面理解图:x代表点绕Re轴的弧度,Re是实轴,Im是虚轴
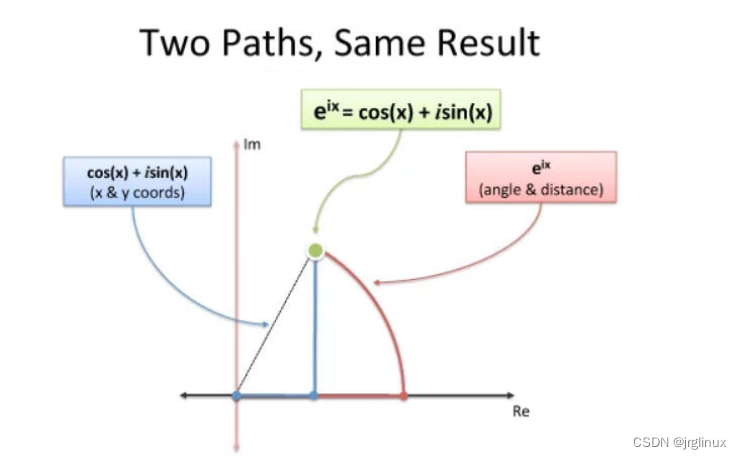
当点在复平面内做圆周运动,便可用欧拉公式来描述。随着时间的改变,复平面内圆周运动轨迹就成了螺旋曲线。
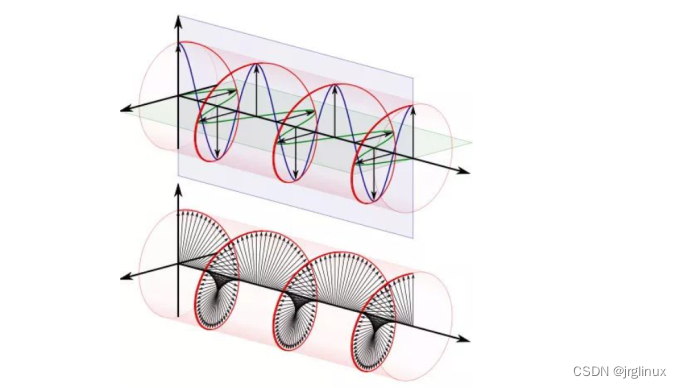
宇宙万物,自旋运动与圆周运动,构成了每个时刻在旋转的浩瀚星系,里面又有个欧拉公式,实在妙哉。
【参考文献】
-
从代数基本定理到超越数:一段经典数学的奇幻之旅/冯承天著.
-
https://betterexplained.com/articles/easy-trig-identities-with-eulers-formula/