1.题目链接:
39. 组合总和
2.解题思路:
2.1.题目要求:
给定一个“无重复数组candidates”和一个“目标和target” ,要求在给定 数组candidates 的范围内,输出和等于 目标和target 的组合,此组合元素可重复。
示例 1: 输入:candidates = [2,3,6,7], target = 7, 所求解集为: [ [7], [2,2,3] ]
2.2.思路:
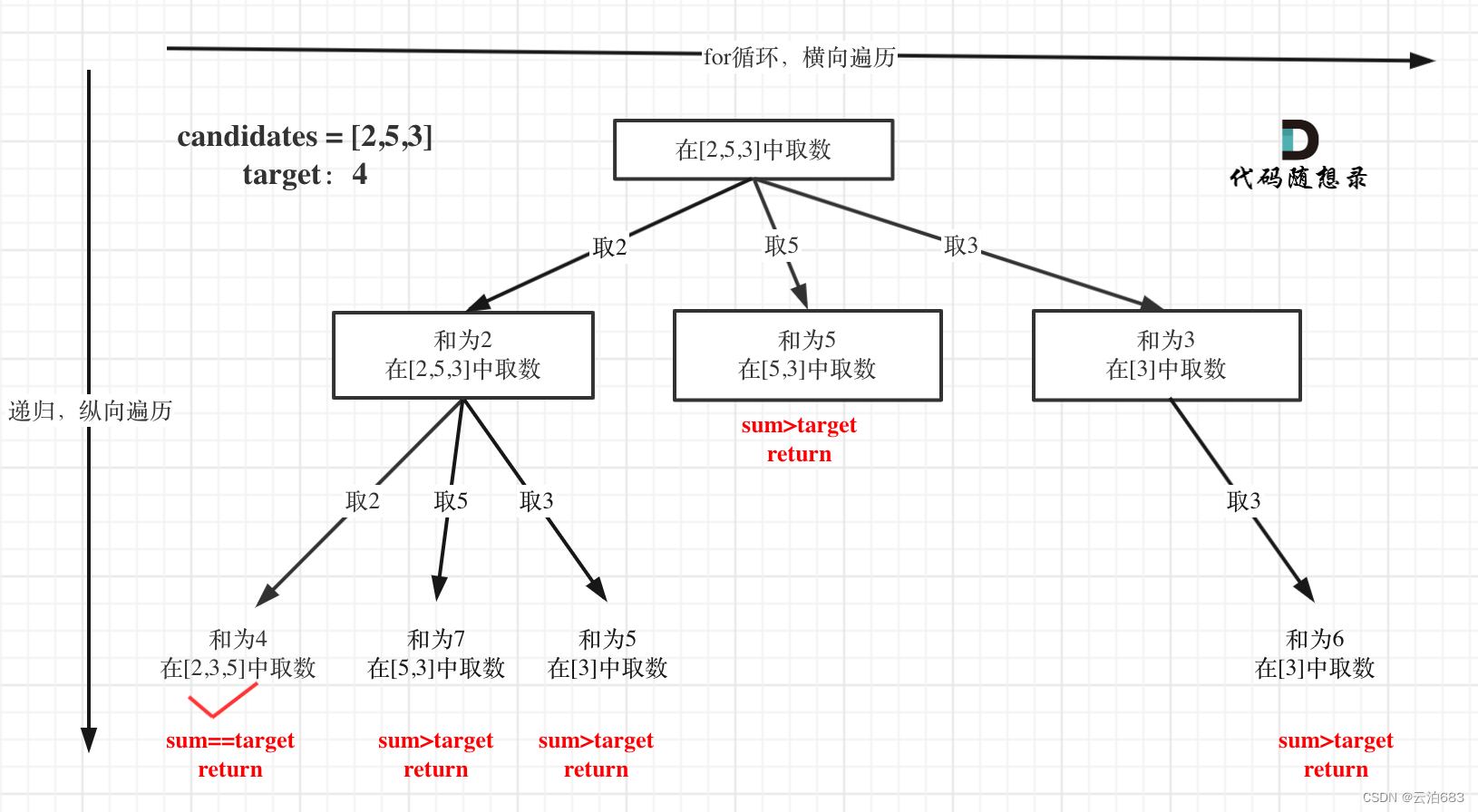
模拟成一个n叉树,终止条件 变成 搜索的和等于目标和
2.3.回溯三部曲:
2.3.1.确定回溯函数参数
定义两个全局变量,一个 一维数组path 暂时存储搜集的结果,一个 二维数组result 存储最终结果集
参数除了默认的 数组candidates 和 目标和target ,还有用于记录搜集递归过程值的sum,还有一个startIndex?感觉用不上这玩意,待会试试看
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
2.3.2.确定终止条件
当 搜集数字的总和sum 等于 目标和target 的时候,可以记录并返回了
同时因为没有层数要求,会不断递归寻找合适的值,所以需要一个条件来限制层数,也就是当总和sum已经大于目标和target的时候。
if (sum > target) return;
if (sum == target) {
result.push_back(path);
return;
}
2.3.3.确定单层遍历逻辑
这里递归到下一层搜索不用像之前那样+1,因为题目说,组合可以重复。
for (int i = startIndex; i < candidates.size(); i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i); // 不用i+1了,表示可以重复读取当前的数
sum -= candidates[i];
path.pop_back();
}
2.4.总代码:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
if (sum > target) {
return;
}
if (sum == target) {
result.push_back(path);
return;
}
for (int i = startIndex; i < candidates.size(); i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i); // 不用i+1了,表示可以重复读取当前的数
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
result.clear();
path.clear();
backtracking(candidates, target, 0, 0);
return result;
}
};
2.5.剪枝优化
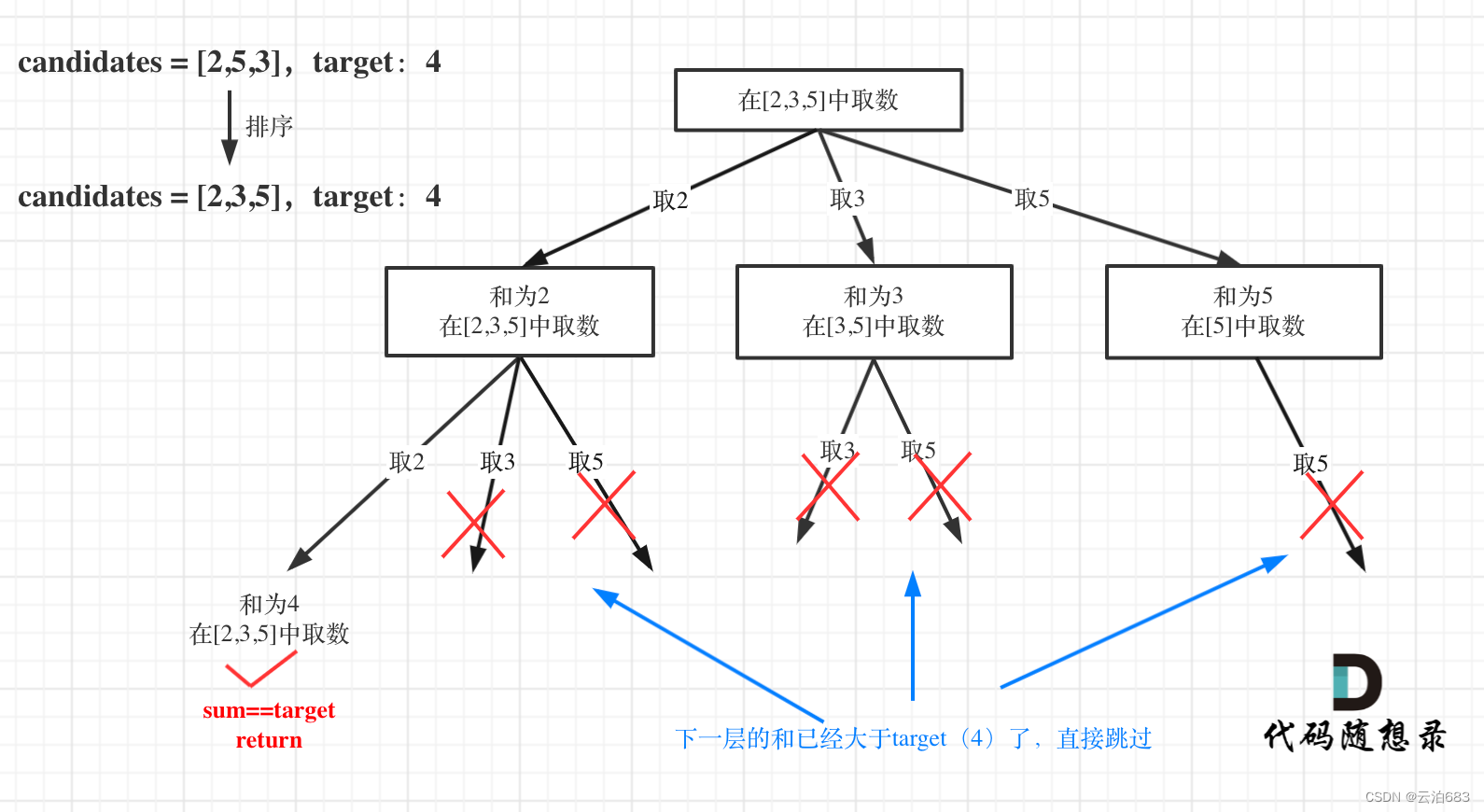
如图所示,当sum > target的时候就会返回,如果可以提前预测下一层的sum 会不会大于 target,如果大于就跳过,这样就可以省去一层遍历了,剪枝成功。
剪枝可以在for循环范围作改动,在范围那提前预测,加上 && sum + candidates[i] <= target ,在预测下一层sum不大于target的前提下继续递归。
注意,剪枝前记得,要先排序,不排序 sum + candidates[i] <= target的代码预测可能不准,因为,如果一开始下一层就遇见很大的数的话(超过target),那这一整层都会被剪掉,这样就缺少了很多组合。
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++)
剪枝代码如下:
class Solution {
private:
vector<vector<int>> result;
vector<int> path;
void backtracking(vector<int>& candidates, int target, int sum, int startIndex) {
if (sum == target) {
result.push_back(path);
return;
}
// 如果 sum + candidates[i] > target 就终止遍历
for (int i = startIndex; i < candidates.size() && sum + candidates[i] <= target; i++) {
sum += candidates[i];
path.push_back(candidates[i]);
backtracking(candidates, target, sum, i);
sum -= candidates[i];
path.pop_back();
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
result.clear();
path.clear();
sort(candidates.begin(), candidates.end()); // 需要排序
backtracking(candidates, target, 0, 0);
return result;
}
};
3.遇见的问题:
3.1starIndex的作用?
写了一遍,一开始感觉是固定每一层递归从0开始。
但下一层递归传的不是starIndex,是 i ?。这是什么原理?
按理来说反正下一层递归 i 默认都是被index赋值等于 0 的,也就是传入啥都可以,不影响
但是这样却报错了,要换成 i 才给过,回忆下过程每一层都是从 0 开始,传入的 i 在我看来根本没意义啊,他起到的作用是什么 ?
哦哦,回看了下之前的 001.组合的代码,那里是 i+1,代表每一次取过的数不再取,哪里的index是用来定位的,
用这里的i类比的话,意思大概就是可以取,取过的数,递归下一层从 i 而不是从0开始,是因为之前的数已经取过了的意思吧
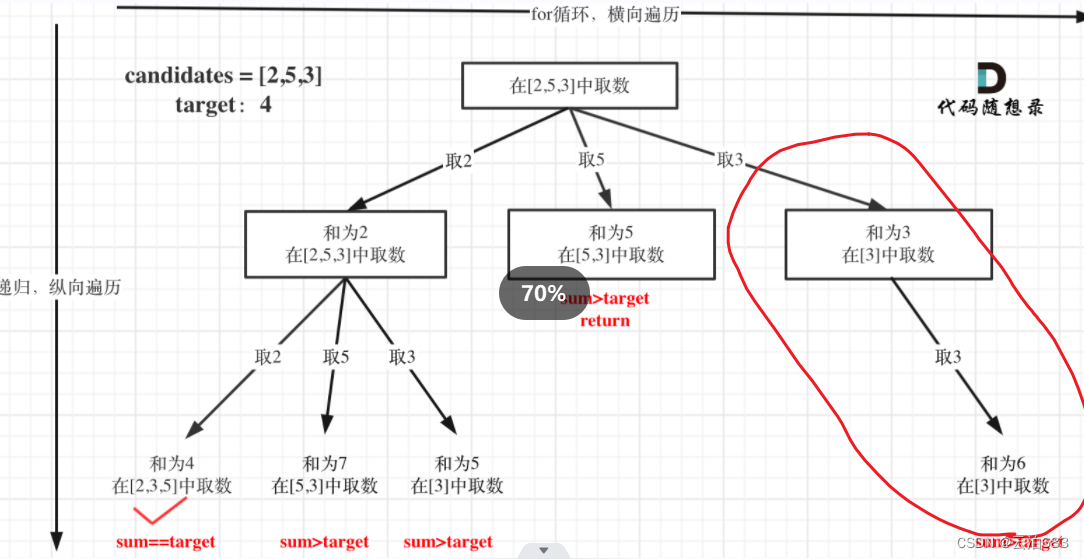
比如画圈这里,2,5已经用过,只能从3取,哦哦,下一层递归的目的是为了避免组合重复出现,第一层已经确认大部分的组合了,后面只是补漏,从 i 取可以避免元素重复。
4.记录:
果然之前的理解还是有很多漏洞,现在补上了(大概..)
与之前题目的不同点:
- 组合没有数量要求
- 元素可无限重复选取