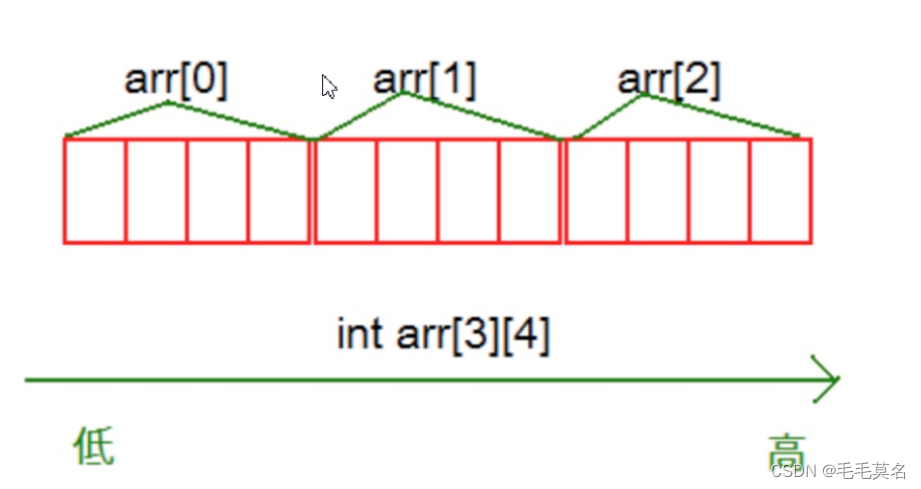
在脚本中通常用Vector3、QUaternion、Transform等类的属性和方法来对物体进行变换，Matrix4x4类通常在一些比较特殊的地方，如对摄像机的非标准投影变换等。本博客主要介绍Matrix4x4类的一些实例和静态方法。

一、Matrix4x4类实例方法

在Matrix4x4类，涉及的实例方法有MultplyPoint方法、MultiplyPoint3x4方法、MultiplyVector方法和SetTRS方法。

1、MultplyPoint方法：投影矩阵变换

(1)基本语法

public VEctor3 MultiplyPoint(VEctor 3 v);

(2)功能说明

此方法的功能用来对点v进行投影矩阵变换。例如，设m1位Matrix4x4实例、v1位Vector3实例，Vector3 v2=m1.MultiplyPoint(v1)，则v2值变换过程如下：v2=v1.m1·M，系统在进行变换时会给v1增加一个w的分量，扩充为四维向量，w默认值为1，而M为投影变换矩阵：

$$M=\left[\begin{array}{cccc}\frac{\cot \Theta }{Aspect}& 0& 0& 0\\ 0& \cot \Theta & 0& 0\\ 0& 0& \frac{f}{f-n}& 1\\ 0& 0& \frac{n\cdot f}{n-f}& 0\end{array}\right]$$
其中f和n为远视口的距离，如图所示，Θ为视口夹角，Aspect为视口的纵横比值。

(3)实例演示

using System.Collections;
using System.Collections.Generic;
using UnityEngine;

public class Aspect_demo : MonoBehaviour
{

    void Start()
    {
        //camera.aspect的默认值即为当前硬件的aspect值
        Debug.Log("camera.aspect的默认值" + GetComponent<Camera>().aspect);
    }


    void OnGUI()
    {
        if (GUI.Button(new Rect(10.0f, 10.0f, 200.0f, 45.0f), "aspect=1.0f"))
        {
            //重置当前摄像机的aspect值
            GetComponent<Camera>().ResetAspect();
            GetComponent<Camera>().aspect = 1.0f;
        }
        if (GUI.Button(new Rect(10.0f, 60.0f, 200.0f, 45.0f), "aspect=2.0f"))
        {
            //重置当前摄像机的aspect值
            GetComponent<Camera>().ResetAspect();
            GetComponent<Camera>().aspect = 2.0f;
        }
        if (GUI.Button(new Rect(10.0f, 110.0f, 200.0f, 45.0f), "aspect还原默认值"))
        {
            //重置当前摄像机的aspect值
            GetComponent<Camera>().ResetAspect();
        }
    }
}

2、MultiplyPoint3x4方法：矩阵变换

(1)基本语法

public VEctor3 MultiplyPoint3x4(VEctor 3 v);

(2)功能说明

此方法的功能是用来对参数值点进行矩阵变换。此方法在对参数v进行矩阵变换时，不涉及投影变换，速度比MultiplyPoint快。例如，设m1为Matrix4x4实例，v1为Vector3实例，则Vector3 v2=m1，MultiplyPoint3线（v1），即为v2=v3*m1，其中v3=(v1，w)，w默认值为1

3、MultiplyVector方法：矩阵变换

(1)基本语法

public VEctor3 MultiplyVector(VEctor 3 v);

(2)功能说明

此方法的功能是用来对方向向量v进行矩阵变换。此方法与方法MultiplyPoint功能类似，但它把v当做方向向量而非坐标点进行变换，当用矩阵与v进行变换时，只是对v的方向进行转换，也即系统会对参与变换的Matrix4x4进行特殊处理：设M为参与变换的Matrix4x4实例，其值为：
$$M=\left[\begin{array}{cccc}m00& m01& m02& m03\\ m10& m11& m12& m13\\ m20& m21& m22& m23\\ m30& m31& m32& m33\end{array}\right]$$

二、Matrix4x4类静态方法

1、Ortho方法：创建正交投影矩阵

2、Perspectice方法：创建透视投影矩阵

(1)基本语法

public static Matrix4x4 Perspective(float fov,float aspect,float zNear,float zFar);

其中参数fov为视口夹角，参数aspect为视口纵横比例，参数zNear为近视口距离，参考zFar为远视口距离。

(2)功能说明

此方法的功能视床架一个透视投影矩阵。若要更改摄像机的透视投影矩阵，可以用如Camera.main.projectionMatrix=Matrix4x4.Perspective(float fov,float aspect,float zNear,float zFar);如果要重置其投影矩阵，需要使用语法
Camera.main.ResetProjectionMatrix();
方法中各个参数图解如图4和图5所示（其中aspect=width/height）