一、背景
在一个理想的连续世界中,任何非线性的东西都可以被线性的东西来拟合,所以理论上线性模型可以模拟物理世界中的绝大多数现象。
线性模型(Linear Model)是机器学习中应用最广泛的模型,指通过样本特征的线性组合来进行预测的模型。给定有d个属性描述的示例,线性模型试图学得一个通过属性的线性组合来进行预测的函数,即:
一般用向量形式写成:
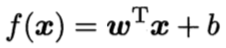
二、线性模型参数求解的本质
不管对 f(x) 施加什么样的变化,从方程求解角度来看,是一个线性方程组。
在这个方程组中,x 是我们已知的,因为我们有训练样本,所以在初始化时,我们的线性方程组看起来是如下形式:
y1 = 1 * w1 + 2 * w2 + .... + 3 * wn; .... yn = 3 * w1 + 4 * w2 + .... + 3 * wn;
每个样本代表线性方程组的一行,样本中完全线性共线的可以约去。
这样,我们就得到了一个 N(样本数) * M(特征维度) 的巨大矩阵。而样本的值和标签即(x,y)共同组成了一个巨大的增广矩阵。注意,是样本组成了系数矩阵,不是我们要求的模型参数!
求解线性模型的参数向量(w,b)就是在求解线性方程组的一个方程解,所有的方程解组成的集合称为线性方程组的解集合。
同时,在机器学习中,我们称 w 和 b 为线性模型的超参数,满足等式条件的(w,b)组合可能不只一种,所有的超参数构成了一个最优参数集合。实际上,根据线性方程组的理论,线性方程组要么有唯一解,要么有无限多的解。
唯一解的条件比较苛刻,在大多数的场景和数据集下,解空间都是无限的,机器学习算法的设计目标就是:
基于一种特定的归纳偏置,选择一个特定的超参数(w,b),使得模型具备最好的泛化能力,机器学习算法的目的不是解方程,而是获得最好的泛化能力。
当超参数通过训练拟合过程确定后,模型就得以确定。
三、线性回归
线性回归(linear regression)试图学得一个线性模型:
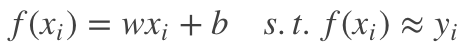
,以尽可能准确地预测实值输出标记。
注意,这里用”尽可能地准确“这个词,是因为在大多数时候,我们是无法得到一个完美拟合所有样本数据的线性方程的,即直接基于输入数据构建的多元线性方程组在大多数时候是无解的。
如下图所示:
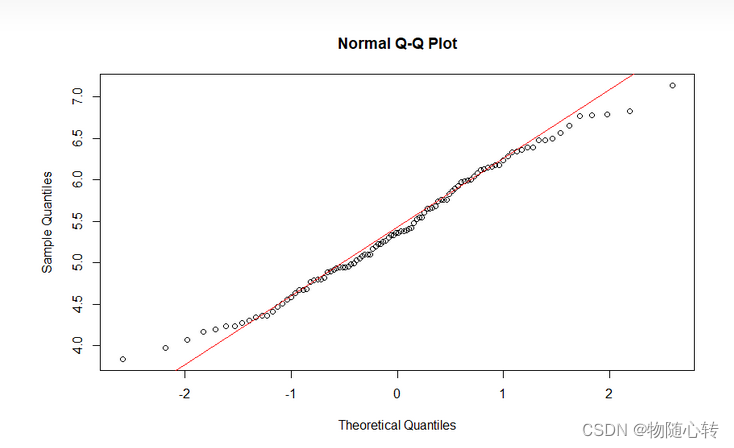
这个时候怎么办呢?数学家高斯发现了最小二乘法,它的主要思想是:寻找一个解向量,它和目标数据点的距离尽可能地小。
所以现代线性回归算法所做的事情是:在一定的线性约束条件下,求解线性目标函数的极值问题,这是一个线性规划问题。
四、损失函数的选择
损失函数用来评价模型的预测值和真实值不一样的程度,损失函数越好,通常模型的性能越好。不同的模型用的损失函数一般也不一样。
我们刚说道,直接基于输入数据求解对应线性方程组是无解的,高斯为了解决这个问题,引入了最小二乘。在此之上,之后的数学家又发展出了多种损失评估函数,其数学形式各异,但其核心思想是一致的。损失函数的选择,本质上就是在选择一种误差评价标准,选择何种损失函数取决于我们如何看待我们的问题场景,以及我们希望得到什么样的解释。
我们讨论主要的常用损失函数:
4.1 最小二乘法
线性模型试图学得
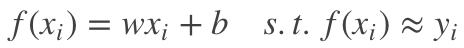
同时在噪声符合高斯分布的假设前提下,均方误差是衡量 f(x) 和 y 之间的差别的最佳损失函数。
因此我们可以试图让均方误差最小化,即:
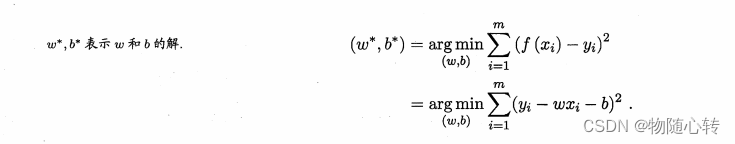
均方误差有非常好的几何意义,它对应了常用的欧几里得距离或简称欧氏距离。基于均方误差误差最小化来进行模型求解的方法称为“最小二乘法(least square method)”。

注意:这里 E(w,b) 是关于 w 和 b 的凸函数,当它关于 w 和 b 的导数均为零时,得到 w 和 b 的最优解。但是对于更高维的线性模型甚至非线性模型,目标函数往往并不是全局凸函数,因此不能继续使用导数为零的方式进行最优解求解,这个时候就需要例如梯度下降法这种递归优化求解算法。
4.2 梯度下降法
线性模型无论多复杂其本质上都是凸函数,凸函数一定可以求得全局最优的极值点,也即最优参数。但是,当函数复杂度继续提高,例如增加了非线性变换之后的复合函数之后,目标函数不一定就是凸函数了(例如深度神经网络),这个时候我们就很难直接求得闭式解,矩阵求逆也不一定可以完成。针对这种复杂函数,GD梯度下降就是一种相对万能通用的迭代式参数求解算法。
我们从某些初始解出发,迭代寻找最优参数值。每次迭代中,我们先计算误差函数在当前点的梯度,然后根据梯度确定搜索方向。例如,由于负梯度方向是函数值下降最快的方向,因此梯度下降法就是沿着负梯度方向搜索最优解.若误差函数在当前点的梯度为零,则已达到局部极小,更新量将为零,因为我们并没有尝试完所有的参数组合,所以不能确定我们得到的局部最小值是否便是全局最小值,选择不同的初始参数组合,可能会找到不同的局部最小值。

下面的h(x)是要拟合的函数,J(theta)损失函数,theta是参数,要迭代求解的值,theta求解出来了那最终要拟合的函数h(theta)就出来了。其中m是训练集的记录条数,j是参数的个数。这里J( θ)中的1/2是为了求导便利.


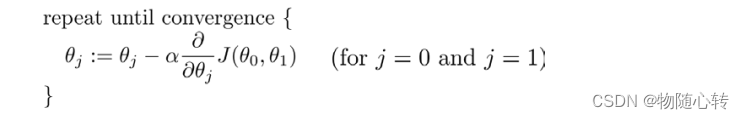
其中 α 是学习率(learning rate) , 它决定了我们沿着能让代价函数下降程度最大的方
向向下迈出的步子有多大,在批量梯度下降中,我们每一次都同时让所有的参数减去学习速
率乘以代价函数的导数。
参考:
Python机器学习之线性模型 - 简书
https://www.cnblogs.com/LittleHann/p/10498579.html#_label0
详解梯度下降算法_梯度下降法_JaysonWong的博客-CSDN博客