1
文法 G 1 G_1 G1为
E → E + T ∣ T T → T ∗ F ∣ F F → ( E ) ∣ i E\rightarrow E+T|T\\ T\rightarrow T*F|F\\ F\rightarrow(E)|i E→E+T∣TT→T∗F∣FF→(E)∣i
请证明 E + T ∗ F E+T*F E+T∗F是他的一个句型(课本写的是E+T*T感觉是印错了),指出它的所有短语,直接短语,句柄
证明过程
E ⇒ E + T ⇒ E + T ∗ F E\Rightarrow E+T\Rightarrow E+T*F E⇒E+T⇒E+T∗F

短语 (句型的语法树的任意一个子树节点组成的符号串都是该句型的短语)
- E + T ∗ F E+T*F E+T∗F (根部E的叶节点符号串)
- T ∗ F T*F T∗F (由E衍生出的根部T的叶节点符号串)
直接短语 (不再包含其他子树的数形成的短语)
- T ∗ F T*F T∗F (由E衍生出的根部T的叶节点符号串) (T不再包含任何子树)
句柄 (直接短语中的最左直接短语)
- T ∗ F T*F T∗F
2
文法 G 2 G_2 G2为
S → a ∣ ∧ ∣ ( T ) T → T , S ∣ S S\rightarrow a|\land|(T)\\ T\rightarrow T,S|S S→a∣∧∣(T)T→T,S∣S
1 给出(a,(a,a))和(((a,a),^,(a)),a)的最左最右推导
(a,(a,a))最左推导
S ⇒ ( T ) ⇒ ( T , S ) ⇒ ( S , S ) ⇒ ( a , S ) ⇒ ( a , ( T ) ) ⇒ ( a , ( S , T ) ) ⇒ ( a , ( T , T ) ) ⇒ ( a , ( a , T ) ) ⇒ ( a , ( a , a ) ) S\Rightarrow (T)\Rightarrow (T,S) \Rightarrow (S,S)\Rightarrow (a,S) \Rightarrow (a,(T))\\\Rightarrow (a,(S,T))\Rightarrow (a,(T,T))\Rightarrow (a,(a,T))\Rightarrow (a,(a,a)) S⇒(T)⇒(T,S)⇒(S,S)⇒(a,S)⇒(a,(T))⇒(a,(S,T))⇒(a,(T,T))⇒(a,(a,T))⇒(a,(a,a))
(a,(a,a))最右推导
S ⇒ ( T ) ⇒ ( T , S ) ⇒ ( T , ( T ) ) ⇒ ( T , ( T , S ) ) ⇒ ( T , ( T , a ) ) ⇒ ( T , ( S , a ) ) ⇒ ( T , ( a , a ) ) ⇒ ( S , ( a , a ) ) ⇒ ( a , ( a , a ) ) S\Rightarrow (T)\Rightarrow (T,S) \Rightarrow (T,(T)) \Rightarrow (T,(T,S)) \Rightarrow (T,(T,a)) \\\Rightarrow (T,(S,a)) \Rightarrow (T,(a,a)) \Rightarrow (S,(a,a)) \Rightarrow (a,(a,a)) S⇒(T)⇒(T,S)⇒(T,(T))⇒(T,(T,S))⇒(T,(T,a))⇒(T,(S,a))⇒(T,(a,a))⇒(S,(a,a))⇒(a,(a,a))
(((a,a),^,(a)),a)最左推导
S ⇒ ( T ) ⇒ ( T , S ) ⇒ ( S , S ) ⇒ ( ( T ) , S ) ⇒ ( ( T , S ) , S ) ⇒ ( ( T , S , S ) , S ) ⇒ ( ( S , S , S ) , S ) ⇒ ( ( ( T ) , S , S ) , S ) ⇒ ( ( ( T , S ) , S , S ) , S ) ⇒ ( ( ( S , S ) , S , S ) , S ) ⇒ ( ( ( a , S ) , S , S ) , S ) ⇒ ( ( ( a , a ) , S , S ) , S ) ⇒ ( ( ( a , a ) , ∧ , S ) , S ) ⇒ ( ( ( a , a ) , ∧ , ( T ) ) , S ) ⇒ ( ( ( a , a ) , ∧ , ( S ) ) , S ) ⇒ ( ( ( a , a ) , ∧ , ( a ) ) , S ) ⇒ ( ( ( a , a ) , ∧ , ( a ) ) , a ) S\Rightarrow (T) \\\Rightarrow (T,S) \\\Rightarrow (S,S) \\\Rightarrow ((T),S) \\\Rightarrow ((T,S),S) \\ \Rightarrow ((T,S,S),S) \\\Rightarrow ((S,S,S),S) \\\Rightarrow (((T),S,S),S) \\ \Rightarrow (((T,S),S,S),S) \\\Rightarrow (((S,S),S,S),S) \\\Rightarrow (((a,S),S,S),S) \\\Rightarrow (((a,a),S,S),S) \\\Rightarrow (((a,a),\land,S),S) \\\Rightarrow (((a,a),\land,(T)),S) \\ \Rightarrow (((a,a),\land,(S)),S) \\\Rightarrow (((a,a),\land,(a)),S) \\\Rightarrow (((a,a),\land,(a)),a) S⇒(T)⇒(T,S)⇒(S,S)⇒((T),S)⇒((T,S),S)⇒((T,S,S),S)⇒((S,S,S),S)⇒(((T),S,S),S)⇒(((T,S),S,S),S)⇒(((S,S),S,S),S)⇒(((a,S),S,S),S)⇒(((a,a),S,S),S)⇒(((a,a),∧,S),S)⇒(((a,a),∧,(T)),S)⇒(((a,a),∧,(S)),S)⇒(((a,a),∧,(a)),S)⇒(((a,a),∧,(a)),a)
(((a,a),^,(a)),a)最右推导
S ⇒ ( T ) ⇒ ( T , S ) ⇒ ( T , a ) ⇒ ( S , a ) ⇒ ( ( T ) , a ) ⇒ ( ( T , S ) , a ) ⇒ ( ( T , ( T ) ) , a ) ⇒ ( ( T , ( S ) ) , a ) ⇒ ( ( T , ( a ) ) , a ) ⇒ ( ( T , S , ( a ) ) , a ) ⇒ ( ( T , ∧ , ( a ) ) , a ) ⇒ ( ( S , ∧ , ( a ) ) , a ) ⇒ ( ( ( T ) , ∧ , ( a ) ) , a ) ⇒ ( ( ( T , S ) , ∧ , ( a ) ) , a ) ⇒ ( ( ( T , a ) , ∧ , ( a ) ) , a ) ⇒ ( ( ( S , a ) , ∧ , ( a ) ) , a ) ⇒ ( ( ( a , a ) , ∧ , ( a ) ) , a ) S\Rightarrow (T) \\\Rightarrow (T,S) \\\Rightarrow (T,a) \\ \Rightarrow (S,a) \\\Rightarrow ((T),a) \\\Rightarrow ((T, S),a) \\\Rightarrow ((T, (T)),a) \\ \Rightarrow ((T, (S)),a) \\\Rightarrow ((T, (a)),a) \\\Rightarrow ((T, S, (a)),a) \\\Rightarrow ((T, \land, (a)),a) \\\Rightarrow ((S, \land, (a)),a) \\\Rightarrow (((T), \land, (a)),a) \\\Rightarrow (((T,S), \land, (a)),a) \\\Rightarrow (((T,a), \land, (a)),a) \\\Rightarrow (((S,a), \land, (a)),a) \\\Rightarrow (((a,a), \land, (a)),a) S⇒(T)⇒(T,S)⇒(T,a)⇒(S,a)⇒((T),a)⇒((T,S),a)⇒((T,(T)),a)⇒((T,(S)),a)⇒((T,(a)),a)⇒((T,S,(a)),a)⇒((T,∧,(a)),a)⇒((S,∧,(a)),a)⇒(((T),∧,(a)),a)⇒(((T,S),∧,(a)),a)⇒(((T,a),∧,(a)),a)⇒(((S,a),∧,(a)),a)⇒(((a,a),∧,(a)),a)
2 (((a,a),^,(a)),a)的规范规约和句柄
规范归约/最左归约是关于是一个最右推导/规范推导的逆过程
由规范推导推出的句型称为规范句型。
于是根据前一问逆向推导得到规范规约
(例子在88页也有)
- ( ( ( a ‾ , a ) , ∧ , ( a ) ) , a ) (((\underline{a},a), \land, (a)),a) (((a,a),∧,(a)),a)
- ( ( ( S ‾ , a ) , ∧ , ( a ) ) , a ) (((\underline{S},a), \land, (a)),a) (((S,a),∧,(a)),a)
- ( ( ( T , a ‾ ) , ∧ , ( a ) ) , a ) (((T,\underline{a}), \land, (a)),a) (((T,a),∧,(a)),a)
- ( ( ( T , S ‾ ) , ∧ , ( a ) ) , a ) (((\underline{T,S}), \land, (a)),a) (((T,S),∧,(a)),a)
- ( ( ( T ) ‾ , ∧ , ( a ) ) , a ) ((\underline{(T)}, \land, (a)),a) (((T),∧,(a)),a)
- ( ( S ‾ , ∧ , ( a ) ) , a ) ((\underline{S}, \land, (a)),a) ((S,∧,(a)),a)
- ( ( T , ∧ ‾ , ( a ) ) , a ) ((T,\underline{\land}, (a)),a) ((T,∧,(a)),a)
- ( ( T , S ‾ , ( a ) ) , a ) ((\underline{T,S}, (a)),a) ((T,S,(a)),a)
- ( ( T , ( a ‾ ) ) , a ) ((T, (\underline{a})),a) ((T,(a)),a)
- ( ( T , ( S ‾ ) ) , a ) ((T, (\underline{S})),a) ((T,(S)),a)
- ( ( T , ( T ) ‾ ) , a ) ((T, \underline{(T)}),a) ((T,(T)),a)
- ( ( T , S ‾ ) , a ) ((\underline{T, S}),a) ((T,S),a)
- ( ( T ) ‾ , a ) (\underline{(T)},a) ((T),a)
- ( S ‾ , a ) (\underline{S},a) (S,a)
- ( T , a ‾ ) (T,\underline{a}) (T,a)
- ( T , S ‾ ) (\underline{T,S}) (T,S)
- ( T ) ‾ \underline{(T)} (T)
- S S S
栈内部的内容需要和输入串的内容一致
| 步骤 | 符号栈 | 输入串 | 动作 |
|---|---|---|---|
| 0 | # | ( ( ( a , a ) , ∧ , ( a ) ) , a ) (((a,a), \land, (a)),a) (((a,a),∧,(a)),a) | initial |
| 1 | # ( ( ( | ( ( a , a ) , ∧ , ( a ) ) , a ) ((a,a), \land, (a)),a) ((a,a),∧,(a)),a) | 移进 |
| 2 | # ( ( (( (( | ( a , a ) , ∧ , ( a ) ) , a ) (a,a), \land, (a)),a) (a,a),∧,(a)),a) | 移进 |
| 3 | # ( ( ( ((( ((( | a , a ) , ∧ , ( a ) ) , a ) a,a), \land, (a)),a) a,a),∧,(a)),a) | 移进 |
| 4 | # ( ( ( a (((a (((a | , a ) , ∧ , ( a ) ) , a ) ,a), \land, (a)),a) ,a),∧,(a)),a) | 移进 |
| 5 | # ( ( ( S (((S (((S | , a ) , ∧ , ( a ) ) , a ) ,a), \land, (a)),a) ,a),∧,(a)),a) | 归约 S → a S\rightarrow a S→a |
| 6 | # ( ( ( T (((T (((T | , a ) , ∧ , ( a ) ) , a ) ,a), \land, (a)),a) ,a),∧,(a)),a) | 归约 T → S T\rightarrow S T→S |
| 7 | # ( ( ( T , (((T, (((T, | a ) , ∧ , ( a ) ) , a ) a), \land, (a)),a) a),∧,(a)),a) | 移进 |
| 8 | # ( ( ( T , a (((T,a (((T,a | ) , ∧ , ( a ) ) , a ) ), \land, (a)),a) ),∧,(a)),a) | 移进 |
| 9 | # ( ( ( T , S (((T,S (((T,S | ) , ∧ , ( a ) ) , a ) ), \land, (a)),a) ),∧,(a)),a) | 归约 S → a S\rightarrow a S→a |
| 10 | # ( ( ( T (((T (((T | ) , ∧ , ( a ) ) , a ) ), \land, (a)),a) ),∧,(a)),a) | 归约 T → T , S T\rightarrow T,S T→T,S |
| 11 | # ( ( ( T ) (((T) (((T) | , ∧ , ( a ) ) , a ) , \land, (a)),a) ,∧,(a)),a) | 移进 |
| 12 | # ( ( S ((S ((S | , ∧ , ( a ) ) , a ) , \land, (a)),a) ,∧,(a)),a) | 规约 S → ( T ) S\rightarrow(T) S→(T) |
| 13 | # ( ( T ((T ((T | , ∧ , ( a ) ) , a ) , \land, (a)),a) ,∧,(a)),a) | 规约 T → S T\rightarrow S T→S |
| 14 | # ( ( T , ((T, ((T, | ∧ , ( a ) ) , a ) \land, (a)),a) ∧,(a)),a) | 移进 |
| 15 | # ( ( T , ∧ ((T,\land ((T,∧ | , ( a ) ) , a ) , (a)),a) ,(a)),a) | 移进 |
| 16 | # ( ( T , S ((T,S ((T,S | , ( a ) ) , a ) , (a)),a) ,(a)),a) | 规约 S → ∧ S\rightarrow \land S→∧ |
| 17 | # ( ( T ((T ((T | , ( a ) ) , a ) , (a)),a) ,(a)),a) | 规约 T → T , S T\rightarrow T,S T→T,S |
| 18 | # ( ( T , ((T, ((T, | ( a ) ) , a ) (a)),a) (a)),a) | 移进 |
| 19 | # ( ( T , ( ((T,( ((T,( | a ) ) , a ) a)),a) a)),a) | 移进 |
| 20 | # ( ( T , ( a ((T,(a ((T,(a | ) ) , a ) )),a) )),a) | 移进 |
| 21 | # ( ( T , ( S ((T,(S ((T,(S | ) ) , a ) )),a) )),a) | 归约 S → a S\rightarrow a S→a |
| 22 | # ( ( T , ( T ((T,(T ((T,(T | ) ) , a ) )),a) )),a) | 归约 T → S T\rightarrow S T→S |
| 23 | # ( ( T , ( T ) ((T,(T) ((T,(T) | ) , a ) ),a) ),a) | 移进 |
| 24 | # ( ( T , S ((T,S ((T,S | ) , a ) ),a) ),a) | S → ( T ) S\rightarrow(T) S→(T) |
| 25 | # ( ( T ((T ((T | ) , a ) ),a) ),a) | T → T , S T\rightarrow T,S T→T,S |
| 26 | # ( ( T ) ((T) ((T) | , a ) ,a) ,a) | 移进 |
| 27 | # ( S (S (S | , a ) ,a) ,a) | 规约 S → ( T ) S\rightarrow (T) S→(T) |
| 28 | # ( T (T (T | , a ) ,a) ,a) | 规约 T → S T\rightarrow S T→S |
| 29 | # ( T , (T, (T, | a ) a) a) | 移进 |
| 30 | # ( T , a (T,a (T,a | ) ) ) | 移进 |
| 31 | # ( T , S (T,S (T,S | ) ) ) | 规约 S → a S\rightarrow a S→a |
| 32 | # ( T (T (T | ) ) ) | 规约 T → T , S T\rightarrow T,S T→T,S |
| 33 | # ( T ) (T) (T) | 移进 | |
| 34 | # S S S | 规约 S → ( T ) S\rightarrow (T) S→(T) |
5
文法
S
→
A
S
∣
b
A
→
S
A
∣
a
S\rightarrow AS|b\\ A\rightarrow SA|a
S→AS∣bA→SA∣a

如果你的起始符号不止一个产生式就得加S’,只有一个产生式可以不加
加入 S’->S
1. 所有的LR(0)项目
S
′
→
⋅
S
(
这个需要自己添加
)
S'\rightarrow \cdot S(这个需要自己添加)
S′→⋅S(这个需要自己添加)
S
→
⋅
A
S
S
→
A
⋅
S
S
→
A
S
⋅
S\rightarrow \cdot AS\quad S\rightarrow A\cdot S\quad S\rightarrow AS \cdot
S→⋅ASS→A⋅SS→AS⋅
S
→
⋅
b
S
→
b
⋅
S\rightarrow \cdot b \quad S\rightarrow b\cdot
S→⋅bS→b⋅
A
→
⋅
S
A
A
→
S
⋅
A
A
→
S
A
⋅
A\rightarrow \cdot SA\quad A\rightarrow S\cdot A\quad A\rightarrow SA \cdot
A→⋅SAA→S⋅AA→SA⋅
A
→
⋅
a
A
→
a
⋅
A\rightarrow \cdot a \quad A\rightarrow a\cdot
A→⋅aA→a⋅
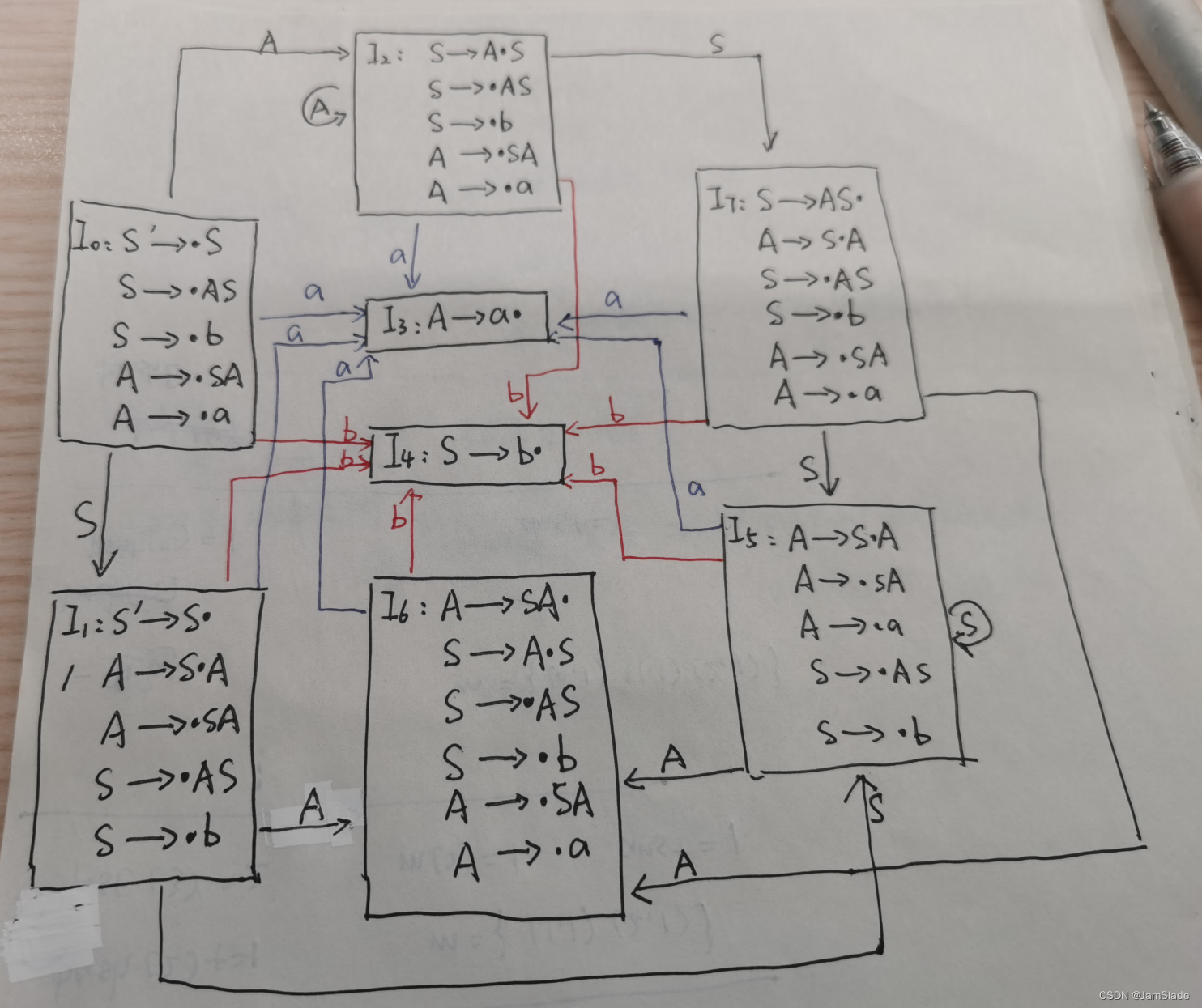
2. 文法的LR(0)项目规范组和识别活前缀的DFA
I 0 I_0 I0
拿出最开始的规约
①
S
′
→
⋅
S
①S'\rightarrow \cdot S
①S′→⋅S
找出所有满足
S
→
⋅
s
o
m
e
t
h
i
n
g
S\rightarrow \cdot something
S→⋅something的情况,根据前文有
②
S
→
⋅
A
S
③
S
→
⋅
b
②S\rightarrow \cdot AS\quad ③S\rightarrow \cdot b
②S→⋅AS③S→⋅b, 此时注意到
S
→
⋅
A
S
S\rightarrow \cdot AS
S→⋅AS,需要再考虑所有满足
A
→
⋅
s
o
m
e
t
h
i
n
g
A\rightarrow \cdot something
A→⋅something的情况
④
A
→
⋅
a
⑤
A
→
⋅
S
A
④A\rightarrow \cdot a\quad⑤ A\rightarrow \cdot SA
④A→⋅a⑤A→⋅SA
于是我们得到
I
0
I_0
I0
①
S
′
→
⋅
S
②
S
→
⋅
A
S
(
由于①获得
)
③
S
→
⋅
b
(
由于①获得
)
④
A
→
⋅
a
(
由于②获得
)
⑤
A
→
⋅
S
A
(
由于②获得
)
①S'\rightarrow \cdot S\\ ②S\rightarrow \cdot AS(由于①获得)\\ ③S\rightarrow \cdot b(由于①获得)\\ ④A\rightarrow \cdot a(由于②获得) \\ ⑤A\rightarrow \cdot SA(由于②获得)
①S′→⋅S②S→⋅AS(由于①获得)③S→⋅b(由于①获得)④A→⋅a(由于②获得)⑤A→⋅SA(由于②获得)
I 1 I_1 I1
观察 I 0 I_0 I0数据,不难发现 ⋅ \cdot ⋅后面接的数据有 S , A , b , a S,A,b,a S,A,b,a,所以可以在 I 0 I_0 I0的基础上状态转移,这里首先转移出S,发现 ⋅ \cdot ⋅后接S的有 ①和⑤ ①和⑤ ①和⑤
I
1
I_1
I1一开始
①
S
′
→
S
⋅
②
A
→
S
⋅
A
①S'\rightarrow S\cdot\\ ②A\rightarrow S\cdot A
①S′→S⋅②A→S⋅A
不难发现①的dot后面没有数据了,所以无法在加项目集,观察②,dot后方为A,所以还需要加
A
→
⋅
s
o
m
e
t
h
i
n
g
A\rightarrow \cdot something
A→⋅something
①
S
′
→
S
⋅
②
A
→
S
⋅
A
③
A
→
⋅
a
(
由于②获得
)
④
A
→
⋅
S
A
(
由于②获得
)
①S'\rightarrow S\cdot\\ ②A\rightarrow S\cdot A\\ ③A\rightarrow \cdot a(由于②获得) \\ ④A\rightarrow \cdot SA(由于②获得)
①S′→S⋅②A→S⋅A③A→⋅a(由于②获得)④A→⋅SA(由于②获得)
再根据④,考虑
S
→
⋅
s
o
m
e
t
h
i
n
g
S\rightarrow \cdot something
S→⋅something
①
S
′
→
S
⋅
②
A
→
S
⋅
A
③
A
→
⋅
a
(
②
)
④
A
→
⋅
S
A
(
②
)
⑤
S
→
⋅
A
S
(
④
)
⑥
S
→
⋅
b
(
④
)
①S'\rightarrow S\cdot\\ ②A\rightarrow S\cdot A\\ ③A\rightarrow \cdot a(②) \\ ④A\rightarrow \cdot SA(②)\\ ⑤S\rightarrow \cdot AS(④)\\ ⑥S\rightarrow \cdot b(④)\\
①S′→S⋅②A→S⋅A③A→⋅a(②)④A→⋅SA(②)⑤S→⋅AS(④)⑥S→⋅b(④)
I 2 I_2 I2
I
0
I_0
I0从A出发,一开始
①
S
→
A
⋅
S
① S\rightarrow A\cdot S
①S→A⋅S
找 S → ⋅ s o m e t h i n g S\rightarrow \cdot something S→⋅something
② S → ⋅ A S ③ S → ⋅ b ②S\rightarrow \cdot AS\\ ③S\rightarrow \cdot b ②S→⋅AS③S→⋅b
找 A → ⋅ s o m e t h i n g A\rightarrow \cdot something A→⋅something
④ A → ⋅ a ⑤ A → ⋅ S A ④A\rightarrow \cdot a\\ ⑤A\rightarrow \cdot SA ④A→⋅a⑤A→⋅SA
没有新的LR(0)项目,结束 I 2 I_2 I2更新
I 3 I_3 I3
I
0
I_0
I0从a出发
A
→
a
⋅
A\rightarrow a\cdot
A→a⋅
I 4 I_4 I4
I
0
I_0
I0从b出发
S
→
b
⋅
S\rightarrow b\cdot
S→b⋅
I 5 I_5 I5
I 1 I_1 I1从a和b出发为 I 3 和 I 4 I_3和I_4 I3和I4,还可以从S和A出发,这里先从S出发
①
A
→
S
⋅
A
① A\rightarrow S\cdot A
①A→S⋅A
根据前面的推导,可以直接把
S
→
⋅
s
o
m
e
t
h
i
n
g
S\rightarrow \cdot something
S→⋅something和
A
→
⋅
s
o
m
e
t
h
i
n
g
A\rightarrow \cdot something
A→⋅something放进去
① A → S ⋅ A ② A → ⋅ a ③ A → ⋅ S A ④ S → ⋅ A S ⑤ S → ⋅ b ① A\rightarrow S\cdot A \\ ②A\rightarrow \cdot a \\ ③A\rightarrow \cdot SA\\ ④S\rightarrow \cdot AS\\ ⑤S\rightarrow \cdot b\\ ①A→S⋅A②A→⋅a③A→⋅SA④S→⋅AS⑤S→⋅b
I 6 I_6 I6
I
1
I_1
I1从A出发
①
A
→
S
A
⋅
②
S
→
A
⋅
S
①A\rightarrow SA\cdot\\ ②S\rightarrow A\cdot S
①A→SA⋅②S→A⋅S
根据前面的推导,可以直接把 S → ⋅ s o m e t h i n g S\rightarrow \cdot something S→⋅something和 A → ⋅ s o m e t h i n g A\rightarrow \cdot something A→⋅something放进去
① A → S A ⋅ ② S → A ⋅ S ③ A → ⋅ a ④ A → ⋅ S A ⑤ S → ⋅ A S ⑥ S → ⋅ b ①A\rightarrow SA\cdot\\ ②S\rightarrow A\cdot S\\ ③A\rightarrow \cdot a \\ ④A\rightarrow \cdot SA\\ ⑤S\rightarrow \cdot AS\\ ⑥S\rightarrow \cdot b\\ ①A→SA⋅②S→A⋅S③A→⋅a④A→⋅SA⑤S→⋅AS⑥S→⋅b
I 7 I_7 I7
观察
I
2
I_2
I2,不难发现A返回自己,a变成
I
3
I_3
I3,b变成
I
4
I_4
I4,剩下S
S
→
A
S
⋅
A
→
S
⋅
A
S\rightarrow AS\cdot \\ A\rightarrow S\cdot A
S→AS⋅A→S⋅A
拓展得到
①
S
→
A
S
⋅
②
A
→
S
⋅
A
③
A
→
⋅
a
④
A
→
⋅
S
A
⑤
S
→
⋅
A
S
⑥
S
→
⋅
b
①S\rightarrow AS\cdot \\ ②A\rightarrow S\cdot A\\ ③A\rightarrow \cdot a \\ ④A\rightarrow \cdot SA\\ ⑤S\rightarrow \cdot AS\\ ⑥S\rightarrow \cdot b\\
①S→AS⋅②A→S⋅A③A→⋅a④A→⋅SA⑤S→⋅AS⑥S→⋅b
剩余的情况
经过检验
I
3
到
I
7
I_3到I_7
I3到I7都无法产生新的状态,不妨写出状态转换对
<
I
0
,
S
,
I
1
>
<
I
0
,
A
,
I
2
>
<
I
0
,
a
,
I
3
>
<
I
0
,
b
,
I
4
>
<
I
1
,
S
,
I
5
>
<
I
1
,
A
,
I
6
>
<
I
1
,
a
,
I
3
>
<
I
1
,
b
,
I
4
>
<
I
2
,
S
,
I
7
>
<
I
2
,
A
,
I
2
>
<
I
2
,
a
,
I
3
>
<
I
2
,
b
,
I
4
>
<
I
5
,
S
,
I
5
>
<
I
5
,
A
,
I
6
>
<
I
5
,
a
,
I
3
>
<
I
5
,
b
,
I
4
>
<
I
6
,
S
,
I
7
>
<
I
6
,
A
,
I
2
>
<
I
6
,
a
,
I
3
>
<
I
6
,
b
,
I
4
>
<
I
7
,
S
,
I
5
>
<
I
7
,
A
,
I
6
>
<
I
7
,
a
,
I
3
>
<
I
7
,
b
,
I
4
>
<I_0,S,I_1>\quad <I_0,A,I_2> \quad <I_0,a,I_3>\quad <I_0,b,I_4>\\ <I_1,S,I_5>\quad <I_1,A,I_6> \quad <I_1,a,I_3>\quad <I_1,b,I_4>\\ <I_2,S,I_7>\quad <I_2,A,I_2> \quad <I_2,a,I_3>\quad <I_2,b,I_4>\\ <I_5,S,I_5>\quad <I_5,A,I_6> \quad <I_5,a,I_3>\quad <I_5,b,I_4>\\ <I_6,S,I_7>\quad <I_6,A,I_2> \quad <I_6,a,I_3>\quad <I_6,b,I_4>\\ <I_7,S,I_5>\quad <I_7,A,I_6> \quad <I_7,a,I_3>\quad <I_7,b,I_4>
<I0,S,I1><I0,A,I2><I0,a,I3><I0,b,I4><I1,S,I5><I1,A,I6><I1,a,I3><I1,b,I4><I2,S,I7><I2,A,I2><I2,a,I3><I2,b,I4><I5,S,I5><I5,A,I6><I5,a,I3><I5,b,I4><I6,S,I7><I6,A,I2><I6,a,I3><I6,b,I4><I7,S,I5><I7,A,I6><I7,a,I3><I7,b,I4>
图如下
3. 是否为SLR?是则列出SLR分析表
首先如何判断?
- 看所有移进项目,点后面跟的终结符作为一个集合
- 找到所有规约项目,每个规约项目的左半部分构造FOLLOW
- 要求1这个集合与2创造出的所有集合两两相交为空
I 1 , I 6 , I 7 I_1,I_6,I_7 I1,I6,I7有移进规约冲突
针对 I 1 I_1 I1的
S
′
→
S
⋅
(
规约
)
A
→
⋅
a
(
移进
)
S
→
⋅
b
(
移进
)
S'\rightarrow S\cdot (规约)\\ A\rightarrow \cdot a (移进)\\ S\rightarrow \cdot b (移进)
S′→S⋅(规约)A→⋅a(移进)S→⋅b(移进)
可以考虑
F
O
L
L
O
W
(
S
′
)
=
{
#
}
FOLLOW(S') = \{\#\}
FOLLOW(S′)={#},不包含 a 或 b.
令
A
C
T
I
O
N
(
1
,
#
)
=
a
c
c
ACTION(1,\#) = acc
ACTION(1,#)=acc解决
I
6
I_6
I6
A
→
S
A
⋅
(
规约
)
A
→
⋅
a
(
移进
)
S
→
⋅
b
(
移进
)
A\rightarrow SA\cdot(规约)\\ A\rightarrow \cdot a (移进)\\ S\rightarrow \cdot b (移进)
A→SA⋅(规约)A→⋅a(移进)S→⋅b(移进)
此时考察规约项目 A → S A ⋅ A\rightarrow SA\cdot A→SA⋅,查看 F O L L O W ( A ) = { a , b } FOLLOW(A) = \{a,b\} FOLLOW(A)={a,b},而后续跟的是终结符 # \# #,无法用SLR解决
I 6 I_6 I6
S → A S ⋅ ( 规约 ) A → ⋅ a ( 移进 ) S → ⋅ b ( 移进 ) S\rightarrow AS\cdot (规约)\\ A\rightarrow \cdot a (移进)\\ S\rightarrow \cdot b (移进) S→AS⋅(规约)A→⋅a(移进)S→⋅b(移进)
考虑规约项目
S
→
A
S
⋅
S\rightarrow AS\cdot
S→AS⋅
F
O
L
L
O
W
(
S
)
=
{
#
,
a
,
b
}
FOLLOW(S) = \{\#,a,b\}
FOLLOW(S)={#,a,b}
同理无法用SLR解决
综上,不是SLR文法
4. 是否为LALR或LR(1)
先构造出拓广文法
S ′ → S S → A S S → b A → S A A → a S'\rightarrow S\\ S\rightarrow AS\\ S\rightarrow b\\ A \rightarrow SA\\ A \rightarrow a S′→SS→ASS→bA→SAA→a
I 0 I_0 I0
首先先将最初始的
S
′
→
⋅
S
S'\rightarrow \cdot S
S′→⋅S放入,由于S后方为空串,所以这里应该为
①
S
′
→
⋅
S
,
#
① S'\rightarrow \cdot S,\#
①S′→⋅S,#
现在由于右边为
⋅
S
\cdot S
⋅S,我们需要把S有关的产生式都放入内部
S
→
A
S
S
→
b
S\rightarrow AS\quad S\rightarrow b
S→ASS→b, 注意到这两个产生式是源于①的,①的展望串为#,所以② ③的展望串接着S
② S → ⋅ A S , # ③ S → ⋅ b , # ② S\rightarrow \cdot AS,\#\\ ③ S\rightarrow \cdot b,\# ②S→⋅AS,#③S→⋅b,#
观察到②的点后为A,A的后方为S,这说明,我们需要将 A A A有关的产生式放进来,并且展望串应该等价于 F I R S T ( S ) = { a , b } FIRST(S) = \{a,b\} FIRST(S)={a,b}
A
→
⋅
S
A
,
a
A
→
⋅
S
A
,
b
A
→
⋅
a
,
a
A
→
⋅
a
,
b
A\rightarrow \cdot SA, a \\ A\rightarrow \cdot SA, b \\ A\rightarrow \cdot a, a \\ A\rightarrow \cdot a, b \\
A→⋅SA,aA→⋅SA,bA→⋅a,aA→⋅a,b
合并成为
④
A
→
⋅
S
A
,
a
/
b
⑤
A
→
⋅
a
,
a
/
b
④A\rightarrow \cdot SA, a/b \\ ⑤A\rightarrow \cdot a, a/b \\
④A→⋅SA,a/b⑤A→⋅a,a/b
根据④我们又可以重新考虑
S
S
S的产生式,并且由于这是因为④引入的产生式,我们要将
F
I
R
S
T
(
A
)
=
{
a
,
b
}
FIRST(A) = \{a,b\}
FIRST(A)={a,b}作为展望串
S
→
⋅
A
S
,
a
/
b
S
→
⋅
b
,
a
/
b
S\rightarrow \cdot AS,a/b\\ S\rightarrow \cdot b,a/b
S→⋅AS,a/bS→⋅b,a/b
与② ③合并得到
I
0
I_0
I0
① S ′ → ⋅ S , # ② S → ⋅ A S , # / a / b ③ S → ⋅ b , # / a / b ④ A → ⋅ S A , a / b ⑤ A → ⋅ a , a / b ① S'\rightarrow \cdot S,\# \\ ②S\rightarrow \cdot AS,\#/a/b\\ ③S\rightarrow \cdot b,\#/a/b\\ ④A\rightarrow \cdot SA, a/b \\ ⑤A\rightarrow \cdot a, a/b \\ ①S′→⋅S,#②S→⋅AS,#/a/b③S→⋅b,#/a/b④A→⋅SA,a/b⑤A→⋅a,a/b
I 1 I_1 I1
从 I 0 I_0 I0出发,识别S
①
S
′
→
S
⋅
,
#
②
A
→
S
⋅
A
,
a
/
b
① S'\rightarrow S\cdot,\# \\ ②A\rightarrow S\cdot A, a/b \\
①S′→S⋅,#②A→S⋅A,a/b
显然①没有啥能拓展的,考虑②,需要考虑所有A的产生式,且展望式包括a,b,并且A后方没有数字了,这时候展望串直接继承a/b
③ A → ⋅ S A , a / b ④ A → ⋅ a , a / b ③A\rightarrow \cdot SA, a/b \\ ④A\rightarrow \cdot a, a/b \\ ③A→⋅SA,a/b④A→⋅a,a/b
再考虑S的产生式 —— 由于S后方为A,不能直接继承③的展望式,而是FIRST(A)作为展望式 (虽然没区别但是本质不太一样)
⑤
S
→
⋅
A
S
,
a
/
b
⑥
S
→
⋅
b
,
a
/
b
⑤S\rightarrow \cdot AS, a/b\\ ⑥S\rightarrow\cdot b, a/b
⑤S→⋅AS,a/b⑥S→⋅b,a/b
考虑⑤,发现新产生的式子和③④一致,结束
I 2 I_2 I2
从 I 0 I_0 I0出发,识别A
① S → A ⋅ S , # / a / b ① S\rightarrow A\cdot S, \#/a/b ①S→A⋅S,#/a/b
S的产生式(①的S后面没有数据,直接继承它的展望式)
②
S
→
⋅
A
S
,
#
/
a
/
b
③
S
→
⋅
b
,
#
/
a
/
b
②S\rightarrow \cdot AS, \#/a/b\\ ③S\rightarrow\cdot b, \#/a/b
②S→⋅AS,#/a/b③S→⋅b,#/a/b
A的产生式由于③被纳入,且A后接着S,展望式为,FIRST(S)
④ A → ⋅ S A , a / b ⑤ A → ⋅ a , a / b ④A\rightarrow \cdot SA, a/b \\ ⑤A\rightarrow \cdot a, a/b \\ ④A→⋅SA,a/b⑤A→⋅a,a/b
I 3 I_3 I3
I 0 I_0 I0识别 a
A → a ⋅ , a / b A\rightarrow a\cdot, a/b A→a⋅,a/b
I 4 I_4 I4
I 0 I_0 I0识别 b
S → b ⋅ , a / b S\rightarrow b\cdot, a/b S→b⋅,a/b
依次类推
得到下图
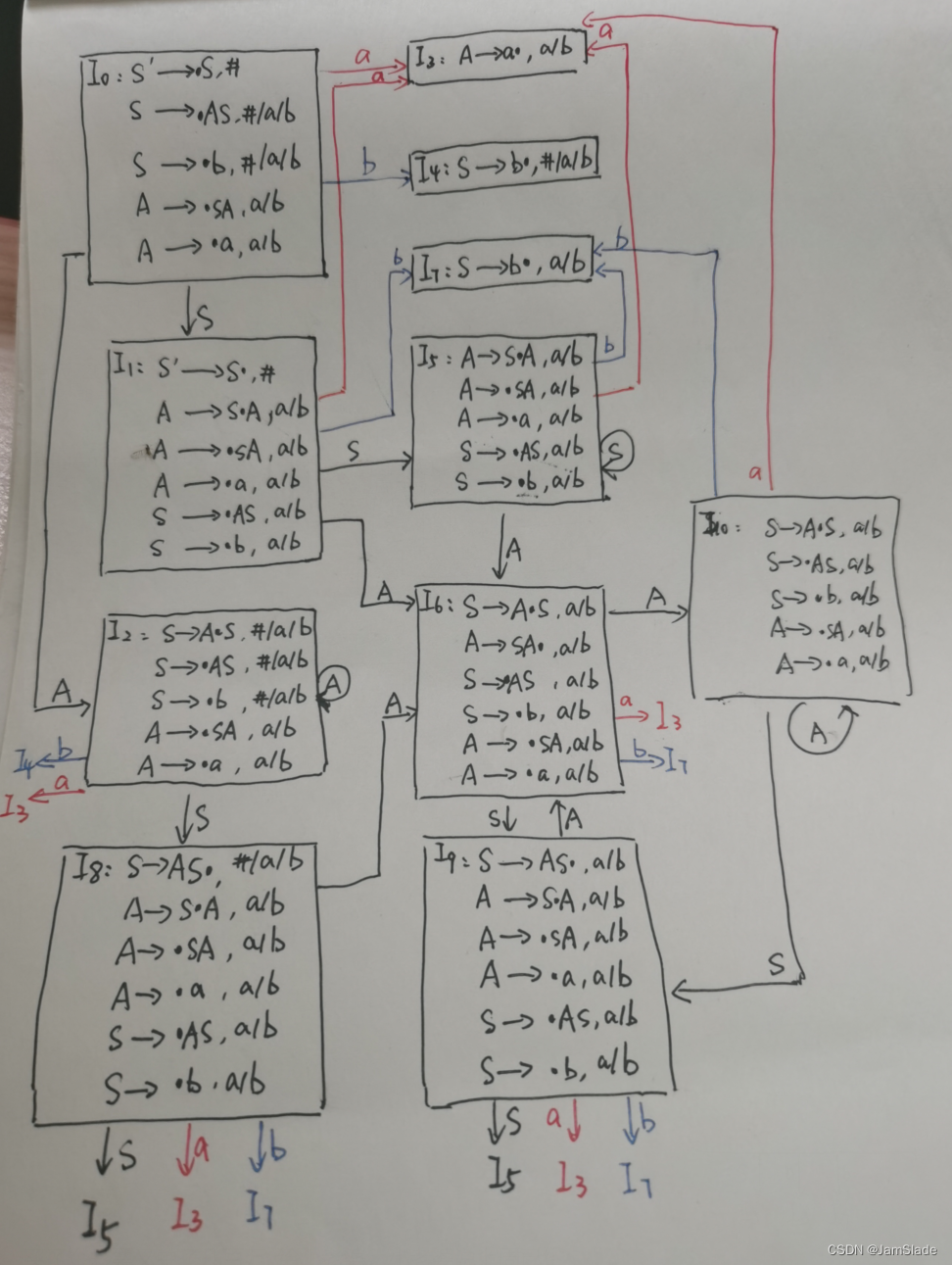
其中 I 6 I_6 I6的 A → S A ⋅ , a / b A\rightarrow SA\cdot, a/b A→SA⋅,a/b要求输入a或b的时候使用 A → S A 规约 A\rightarrow SA规约 A→SA规约
但是 S → ⋅ b , a / b A → ⋅ a , a / b S\rightarrow \cdot b, a/b\quad A\rightarrow \cdot a, a/b S→⋅b,a/bA→⋅a,a/b要求移进,冲突,所以不是 L R ( 1 ) LR(1) LR(1)文法
证明下面的文法SLR(1) 不是LR(0)
S → A A → A b ∣ b B a B → a A c ∣ a ∣ a A b S\rightarrow A\\ A\rightarrow Ab|bBa\\ B\rightarrow aAc|a|aAb S→AA→Ab∣bBaB→aAc∣a∣aAb

状态2存在 移进规约冲突(点·的前方完全一样,后缀不一样)
S
→
A
⋅
A
→
A
⋅
b
S\rightarrow A\cdot \\ A\rightarrow A\cdot b
S→A⋅A→A⋅b
状态5存在 移进规约冲突(点·的前方完全一样,后缀不一样)
B
→
a
⋅
A
c
B
→
a
⋅
B
→
a
⋅
A
b
B\rightarrow a\cdot Ac \\ B\rightarrow a\cdot \\ B\rightarrow a\cdot Ab
B→a⋅AcB→a⋅B→a⋅Ab
状态9存在规约规约冲突(点的前方的后缀(完全/部分)相同)
B → a A b ⋅ A → A b ⋅ B\rightarrow aAb\cdot \\ A\rightarrow Ab\cdot B→aAb⋅A→Ab⋅
所以他不是LR0文法

对于 I 2 I_2 I2
F O L L O W ( S ) = { # } 我们有 F O L L O W ( S ) ∩ { b } = ∅ 可以令 A C T I O N ( 2 , # ) = r 1 , A C T I O N ( 2 , b ) = S 6 FOLLOW(S) = \{\#\}我们有FOLLOW(S)\cap \{b\} = \empty \quad 可以令ACTION(2,\#) = r_1, ACTION(2,b) = S_6 FOLLOW(S)={#}我们有FOLLOW(S)∩{b}=∅可以令ACTION(2,#)=r1,ACTION(2,b)=S6
I 5 I_5 I5
F O L L O W ( B ) = { a } 显然他和 { ϵ } 交集为 ∅ , 令 A C T I O N ( 5 , a ) = r 5 FOLLOW(B) = \{a\}显然他和\{\epsilon\}交集为\empty, 令ACTION(5,a) = r_5 FOLLOW(B)={a}显然他和{ϵ}交集为∅,令ACTION(5,a)=r5
I 9 I_9 I9
需要考虑产生式A和B
F
O
L
L
O
W
(
A
)
=
{
#
,
b
,
c
}
FOLLOW(A) = \{\#,b,c\}
FOLLOW(A)={#,b,c}
F O L L O W ( A ) ∪ F O L L O W ( B ) = ∅ FOLLOW(A)\cup FOLLOW(B) = \empty FOLLOW(A)∪FOLLOW(B)=∅
得到SLR(1)分析表
| ACTION | GOTO | |||||
| a | b | c | # | A | B | |
| 0 | S2 | 1 | ||||
| 1 | S3 | ACC | ||||
| 2 | S5 | 4 | ||||
| 3 | R1 | R1 | R1 | |||
| 4 | S6 | |||||
| 5 | R4 | S2 | 7 | |||
| 6 | R2 | R2 | R2 | |||
| 7 | S9 | S8 | ||||
| 8 | R5 | |||||
| 9 | R5 | R1 | R1 | R1 | ||
没重复定义,为SLR1文法
addition
拓广文法
S ′ → S S → i C t S S → i C t S e S S → a C → b S'\rightarrow S\\ S\rightarrow iCtS \\ S \rightarrow iCtSeS \\ S \rightarrow a \\ C \rightarrow b S′→SS→iCtSS→iCtSeSS→aC→b
LR0规范族
I
0
I_0
I0
S
′
→
⋅
S
S
→
⋅
i
C
t
S
S
→
⋅
i
C
t
S
e
S
S
→
⋅
a
S'\rightarrow \cdot S\\ S\rightarrow \cdot iCtS \\ S \rightarrow \cdot iCtSeS \\ S \rightarrow \cdot a
S′→⋅SS→⋅iCtSS→⋅iCtSeSS→⋅a
I
1
I_1
I1
S
′
→
S
⋅
S'\rightarrow S\cdot
S′→S⋅
I 2 I_2 I2
S ′ → a ⋅ S'\rightarrow a\cdot S′→a⋅
I 3 I_3 I3
S → i ⋅ C t S S → i ⋅ C t S e S C → ⋅ b S\rightarrow i\cdot CtS \\ S \rightarrow i\cdot CtSeS \\ C \rightarrow \cdot b S→i⋅CtSS→i⋅CtSeSC→⋅b
I
4
I_4
I4
C
→
b
⋅
C \rightarrow b \cdot
C→b⋅
I 5 I_5 I5
S → i C ⋅ t S S → i C ⋅ t S e S S\rightarrow i C\cdot tS \\ S \rightarrow i C\cdot tSeS \\ S→iC⋅tSS→iC⋅tSeS
I 6 I_6 I6
S → i C t ⋅ S S → i C t ⋅ S e S S → ⋅ i C t S S → ⋅ i C t S e S S → ⋅ a S\rightarrow i C t\cdot S \\ S \rightarrow i C t \cdot SeS \\ S\rightarrow \cdot iCtS \\ S \rightarrow \cdot iCtSeS \\ S \rightarrow \cdot a S→iCt⋅SS→iCt⋅SeSS→⋅iCtSS→⋅iCtSeSS→⋅a
I 7 I_7 I7
S → i C t S ⋅ S → i C t S ⋅ e S S\rightarrow i C t S\cdot \\ S \rightarrow i C t S\cdot eS S→iCtS⋅S→iCtS⋅eS
I
8
I_8
I8
S
→
i
C
t
S
e
⋅
S
S
→
⋅
i
C
t
S
S
→
⋅
i
C
t
S
e
S
S
→
⋅
a
S \rightarrow i C t S e\cdot S S\rightarrow \cdot iCtS \\ S \rightarrow \cdot iCtSeS \\ S \rightarrow \cdot a
S→iCtSe⋅SS→⋅iCtSS→⋅iCtSeSS→⋅a
I
9
I_9
I9
S
→
i
C
t
S
e
S
⋅
S \rightarrow i C t S e S\cdot
S→iCtSeS⋅
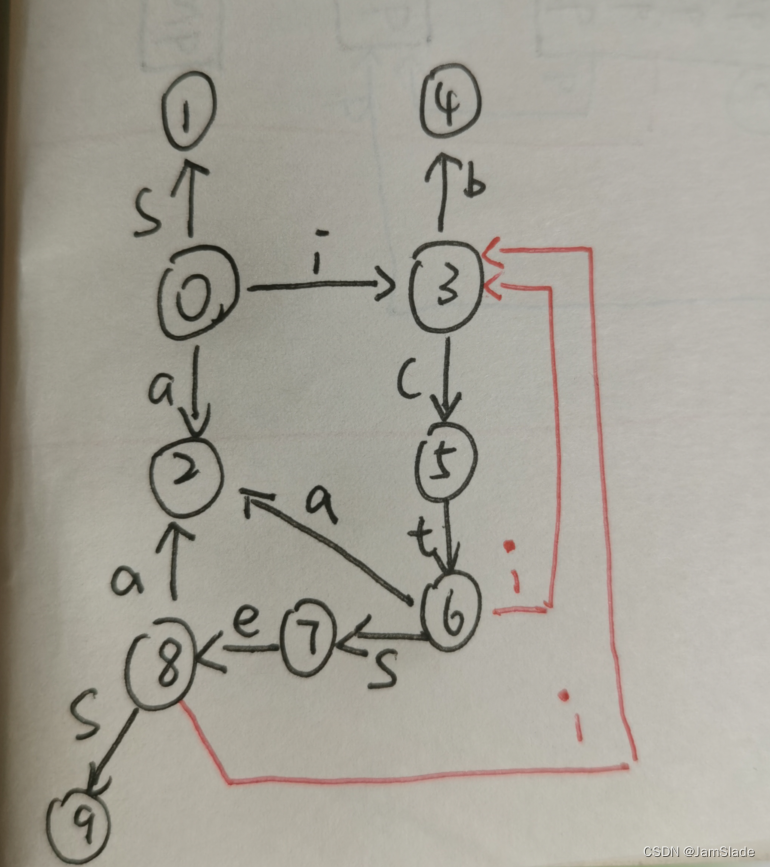
| ACTION | GOTO | |||||||
| i | t | e | a | b | # | S | C | |
| 0 | s3 | s2 | 1 | |||||
| 0 | acc | |||||||
| 2 | r3 | r3 | r3 | r3 | r3 | r3 | ||
| 3 | s4 | 5 | ||||||
| 4 | r4 | r4 | r4 | r4 | r4 | r4 | ||
| 5 | s6 | |||||||
| 6 | s3 | s2 | 7 | |||||
| 7 | r1 | r1 | s8 | r1 | r1 | r1 | ||
| 8 | s3 | s2 | 9 | |||||
| 9 | r2 | r2 | r2 | r2 | r2 | r2 | ||





![【PWN刷题__ret2text】[BJDCTF 2020]babystack](https://img-blog.csdnimg.cn/1ab107b013584c0c973b5251a57fb9f0.png)