1 章节概述

运筹学是一门专门的学科，博大精深，在我们信息系统项目管理师考试中通常会考察3-4分，且计算量很大， 如果花大量时间专门去复习它，性价比不高，并且这部分题目你如果不复习，依靠一些常识以及你的一些基础，足够解题！
【复习建议】：复习时在运筹学上花的时间要适可而止，没有太多时间的，重点掌握我们视频课里的题型即可。但一定要会举一反三。历年真题及详细解析必须搞懂；
◆ 常见题型1-2分+正确思路或代入法解题1-2分+运气
◆ 思路比记住以往考题更重要
◆ 优先考虑看能不能用代入法实在没思路，看能不能用穷举法
◆ 能用某种计算思路凑对答案选项的，可以优先选
◆ 注意：很多题的计算方法并不只有一种!
◆ 尽量得分，实在不会，穷举法，没有时间的话就猜吧，B或者C，哈哈！
➢ 运筹学中常考的有最短和最长路径问题、线性规划的问题、最小生成树、匈牙利法、最大流量、后悔值的问题、传输运输学解决资源分配！希望大家这个7个必须掌握！
➢ 其他的类型的题目一般可以通过穷举法去解题，如果这里实在有困难，可以放弃处理！.

1.1 运筹学计算涉及到的题型

序	常考问题	说明	重要程度
1	线性规划	如：最大利润的生产安排，列方程组求解	熟练掌握
2	动态规划	如：最大利润的分配方案安排	掌握
3	最小生成树	如：改造路线最小长度方案	熟练掌握
4	匈牙利法	如：每人只能做一项任务，如何进行任务的分配	熟练掌握
5	最短（长）路径问题	如：计算网络图最短路径;路径上最少花费;复杂图里计算最长路径、关键路径	熟练掌握
6	网络与最大流量	如：最大运力计算	掌握
7	决策论	不确定型决策：如乐观主义、悲观主义、折中主义、等可能、后悔值准则等;灵敏度分析	熟练掌握
8	伏格尔法	如：涉及需求量和供给量，供给如何分配到需求总费用最低	掌握
9	加工顺序最优安排	车床铣床、需求设计顺序开工最优工序安排问题：参见视频课《时标网络图专题》	掌握
10	其他/总结	参见计算题总结	掌握

2 最优的函数值

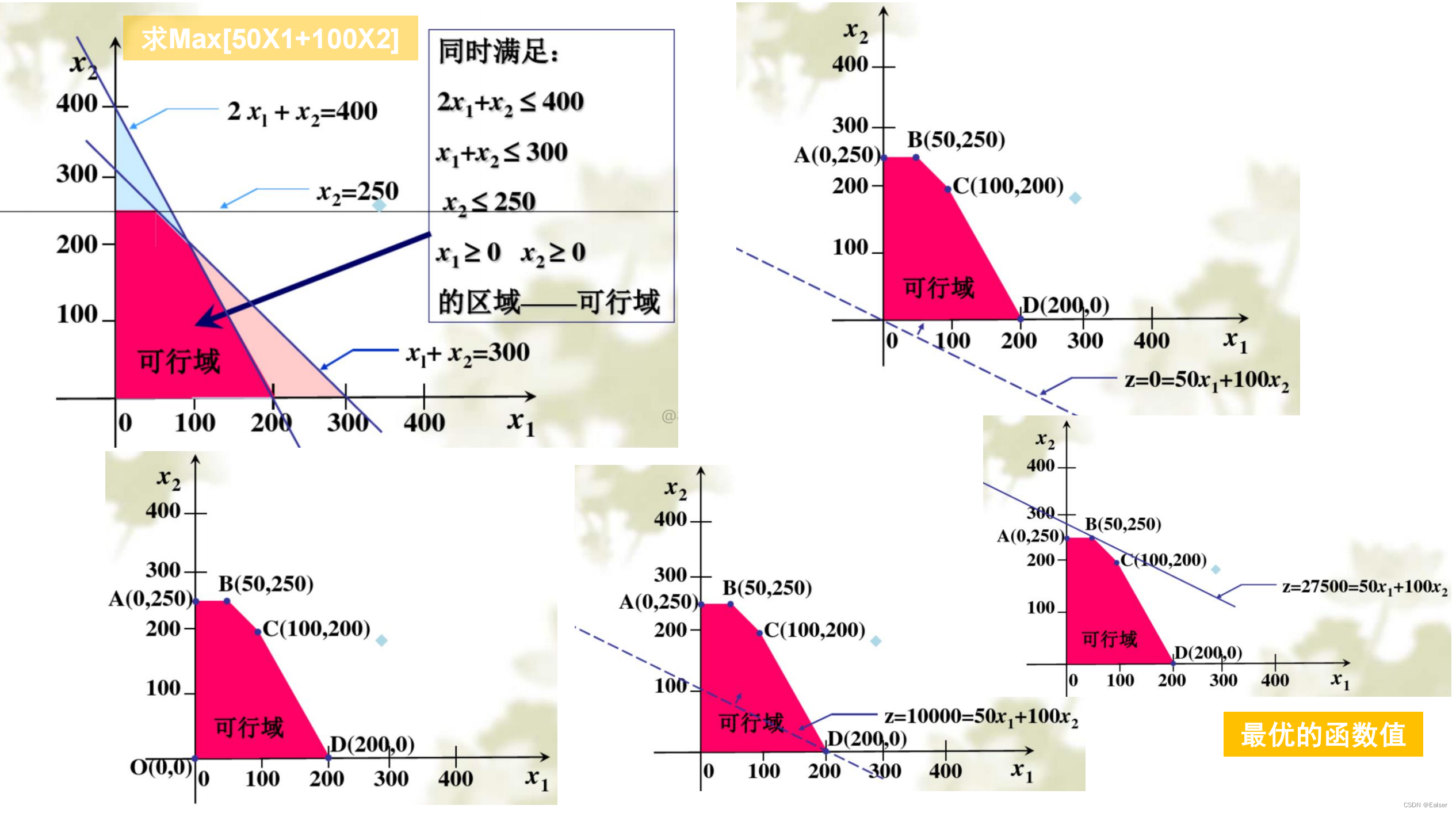
3 线性规划

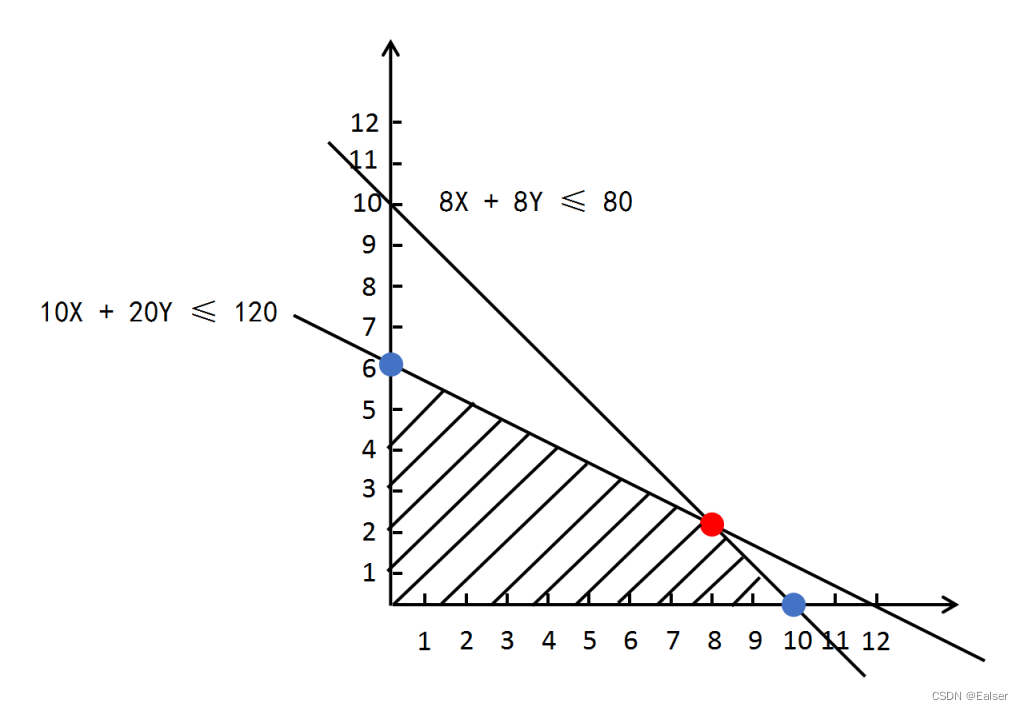
题1

【例1-10上】
某工厂生产两种产品S和K，受到原材料供应和设备加工工时的限制。单件产品的利润、原材料消耗及加工工时如下表所示。为获得最大利润，S应生产（）件。 P875-877/883

A.7 B.8 C.9 D.10

题2

【例2-21下】
已知某公司生产AB两种产品，其中生产1件A产品需要1个单位的甲资源，3个单位的丙资源；
生产1件B产品需要2个单位的乙资源和2个单位的丙资源。已知现有甲乙丙三种资源4个单位、12个单位和18个单位。通过市场预测，可知A产品的单位市场利润为2元，B产品的单位市场利润为5元。该公司获得最大的市场利润应生产A产品（68）件，此时（69）资源仍有剩余。
（68）A.0 B.2 C.4 D.6
（69）A.甲 B.乙 C.丙 D.甲及丙

题3

【例3-22上】
某炼油厂每季度需供应合同单位汽油15吨，煤油12吨，重油12吨，该厂从甲乙两处运回原油提炼，已知两处炼油成分如表所示，从甲处采购原油价格为2000元/吨，乙处为2900元/吨，为了使成本最低，炼油厂应从甲处购（66）吨，乙处采购（67）吨。

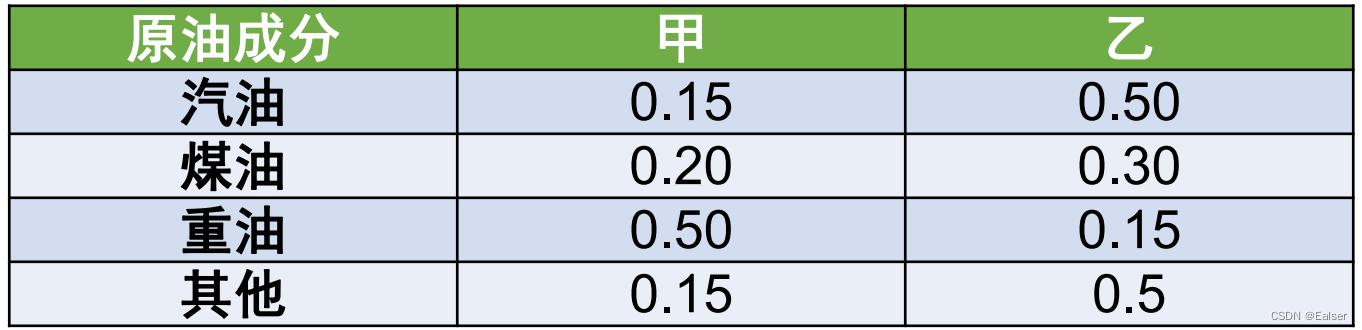
（66）A.15 B.20 C.25 D.30
（67）A.20 B.25 C.30 D.35

4 动态规划 投资收益最大的问题

【例4-11下】某公司现有400 万元用于投资甲、乙、丙三个项目，投资额以百元为单位， 知甲、乙、丙三项投资的可能方案及相应获得的收益如下表所示:则该公司能够获得的最大收益值是（ ）百万元。

A.17 B.18 C.20 D.21
—穷举法去解题也是不错的方法

5 最小生成树

题1

【例5-14下】
煤气公司想要在某地区高层住宅楼之间铺设煤气管道并与主管道相连，位置如下图所示，节点代表各住宅的楼和主管道位置，线上数字代表两节点间距离（单位:百米），则煤气公司铺设的管道总长最短为（）米。
A.1800 B.2200 C.2000 D.2100

题2

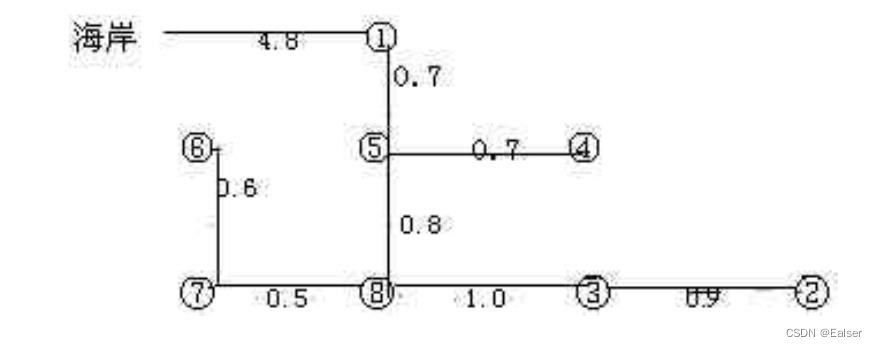
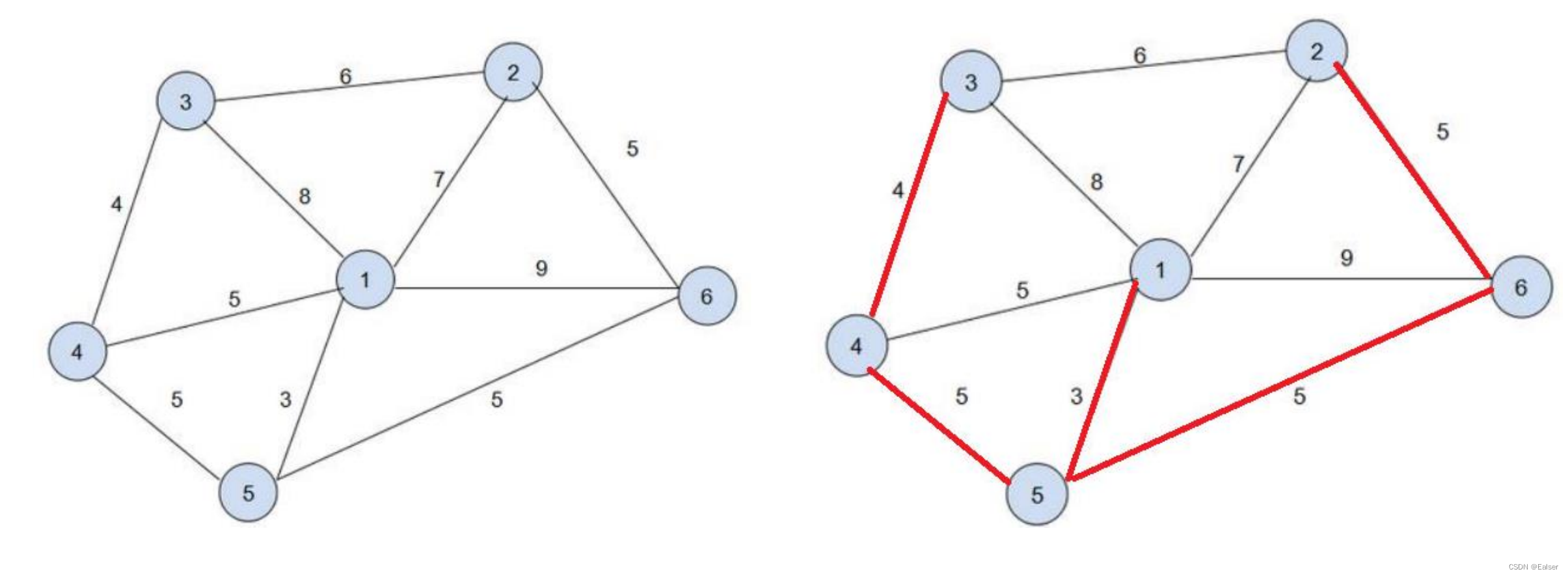
【例6-19上】
有8口海上油井，相互间距离如下表所示（单位:海里）。其中1号井离海岸最短长度，为5海里，先要从海岸经1号井铺设油管将各井连接起来，则铺设输油管道的最短长度（）海里。

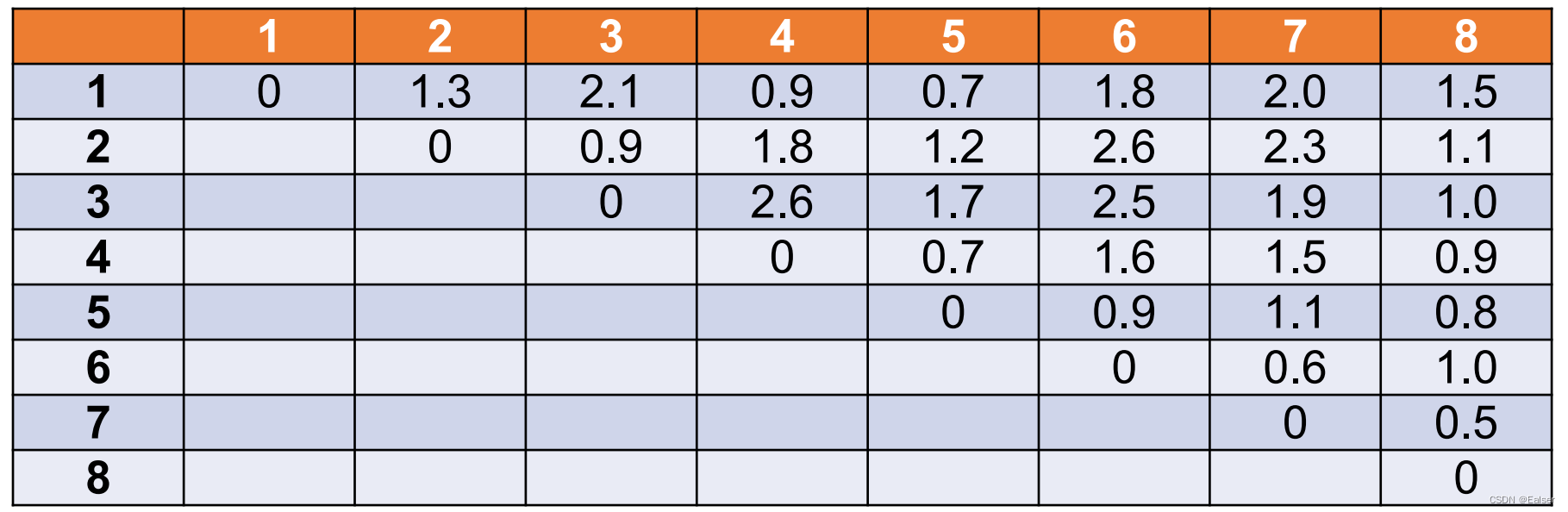
A.9.1 B.9.2 C.10.1 D.10.2

首先定位问题，这属于管理科学及运筹学基础知识中的最小生成树问题。
解法如下:
1）根据上表画出个节点，但不建议将节点之间用线连接，如果连接后，会发现很乱，会看不清楚，考试的时候，图尽量用铅笔在草稿纸上画:
2）然后用「贪心算法」，根据题干给的表，找出各短边、用铅笔在图上画出，判断各点是否连通，最终得出下图:
3）最后算出上图中长度合计:0.7+0.9+1.0+0.7+0.8+0.6+0.5=5.2海里，再加上1号井离海岸最短长度为5海里，所以为10.2海里。 考试的时候做这样的题需要耐心，建议是放到最后来做。用铅笔画图是为了容易擦除。

题3

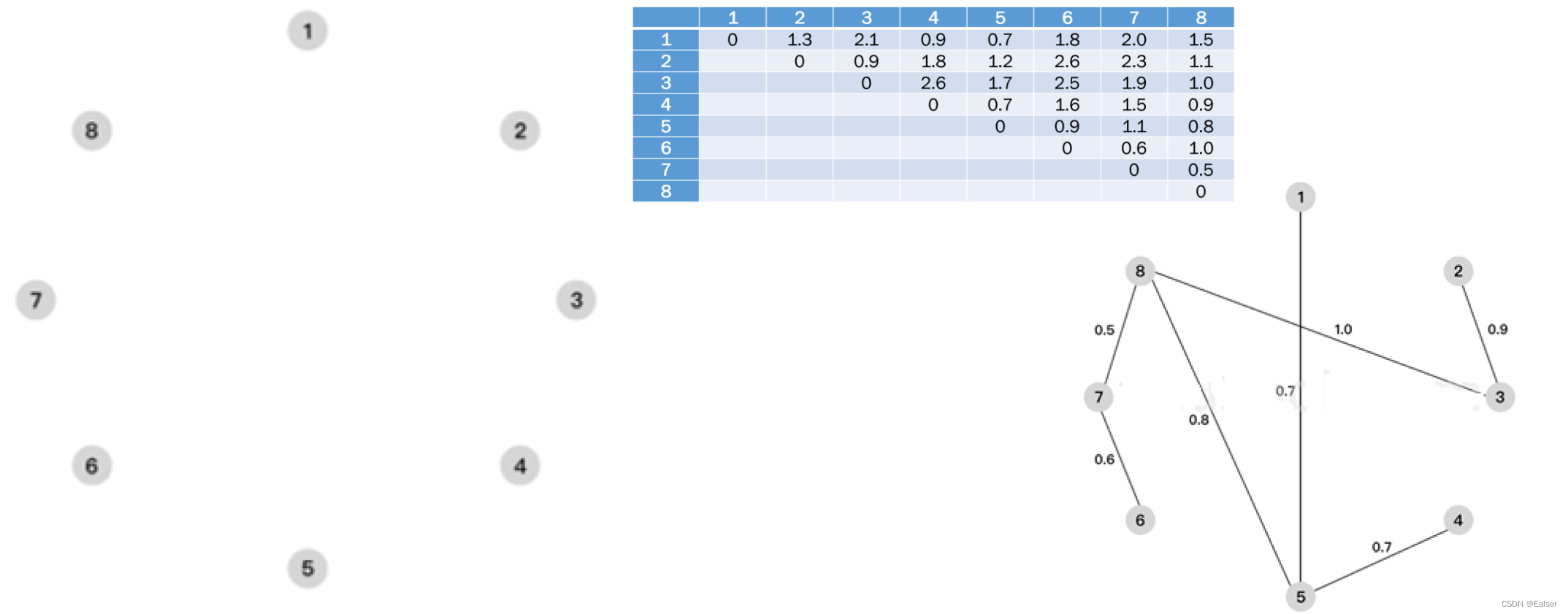
【例7-19下】
下图为某地区的通信线路图，图中节点为8个城市，节点间标识的数字为城市间拟铺设通信线路的长度，为了保持8个城市通讯连接，则至少铺设（）千米的线路。

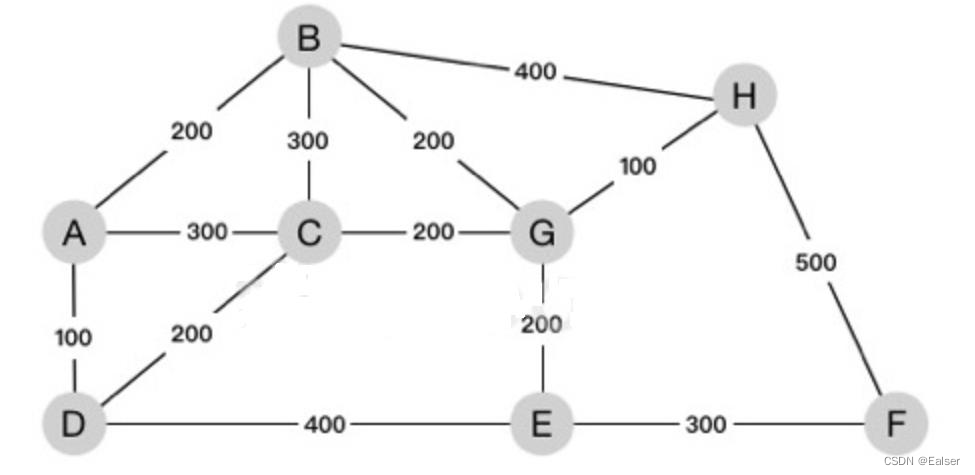
A.1000 B.1100 C.1200 D.1300

6 匈牙利法

题1

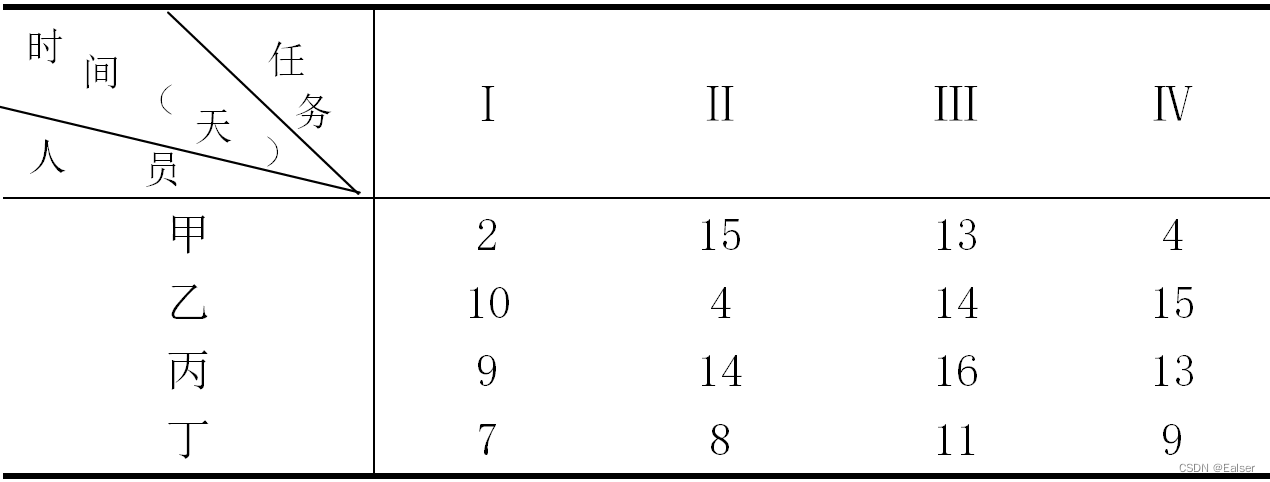
【例8-10下】某项目有I、III 、III、 IV 四项不同任务，恰有甲、乙、丙、丁四个人去完成各项不同的任务，由于任务性质及每人的技术水平不同，他们完成各项任务所需时间也不同，具体如下表所示:项目要求每个人只能完成一项任务，为了使项目花费的总时间最短，应该指派丁完成（）任务。

A.I B.II C.III D.IV

解题：
采用行列矩阵法解答此题，根据表中给定的数据，先用该数据减每行的最小值，得出:

再用该矩阵减每列的最小值，得出:

结论:根据该矩阵中0的位置判断，乙和丙的位置固定了，乙为II，丙为I，则甲只能为IV(甲可以为I或IV，但I已经确定为丙)，故丁为III。

题2

【例9-21下】分配甲、乙、丙、丁四人去完成五项任务。每人完成各项任务时间如表所示，由于任务多于人数，故其中有1人可兼完成2项任务，其余3人每人完成一项。为了花费时间最少，（）应该完成两项任务。

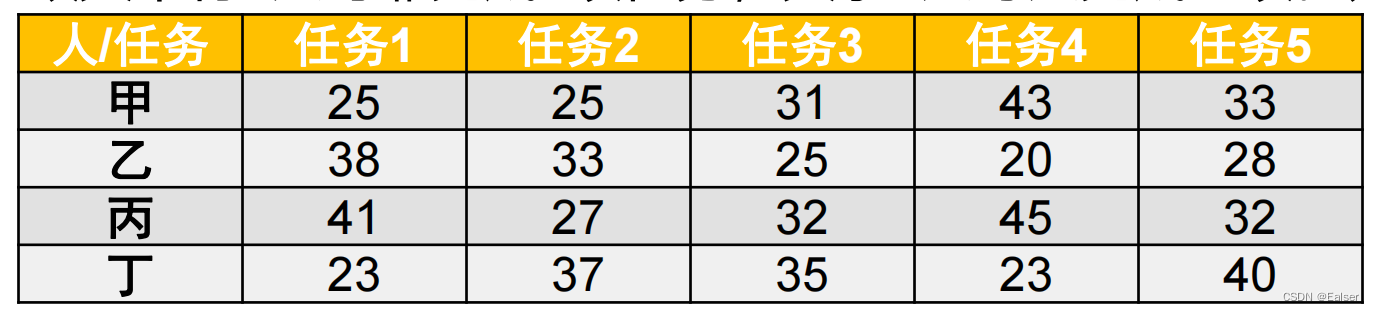
A.甲 B.乙 C.丙 D.丁

解决：

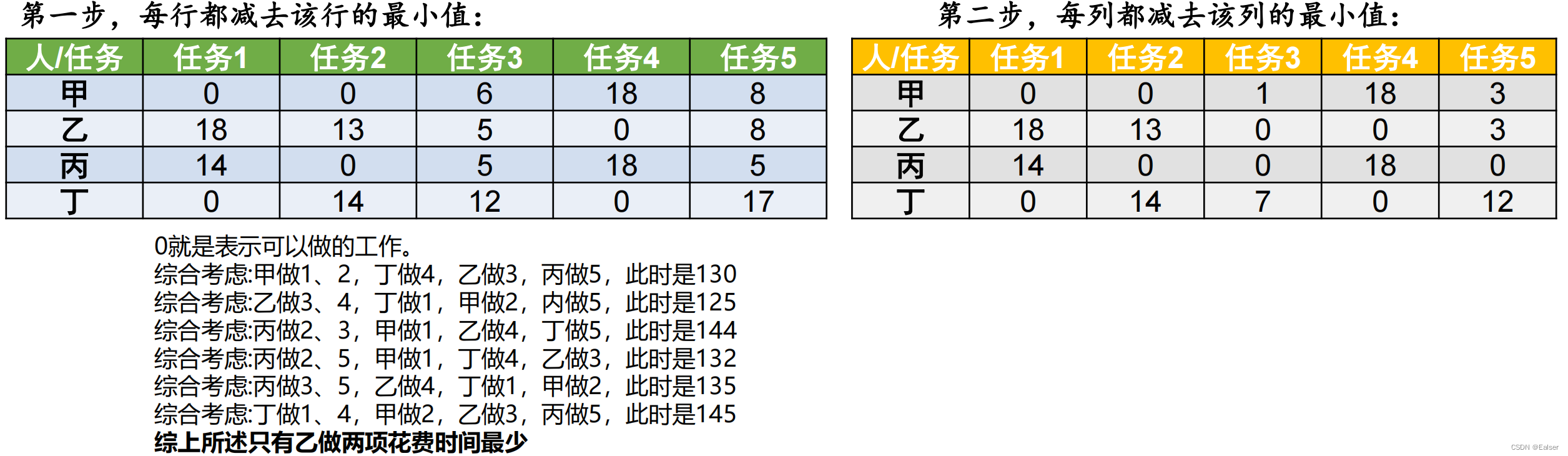
7 最短最长路径问题

题1

【例10-13上】下图中，从A到E的最短长度是（）（图中每条旁的数字为该条边的长度）。

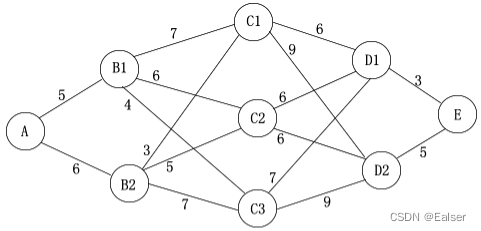
A、17 B、18 C、19 D、20

题2

【例11-14上】下图中，从①到⑧的最短路径有（）条。

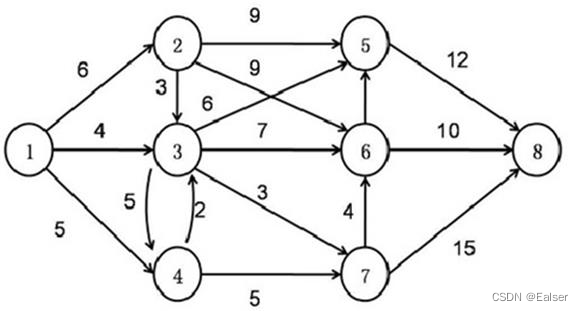
A.1 B.2 C.3 D.4

题3

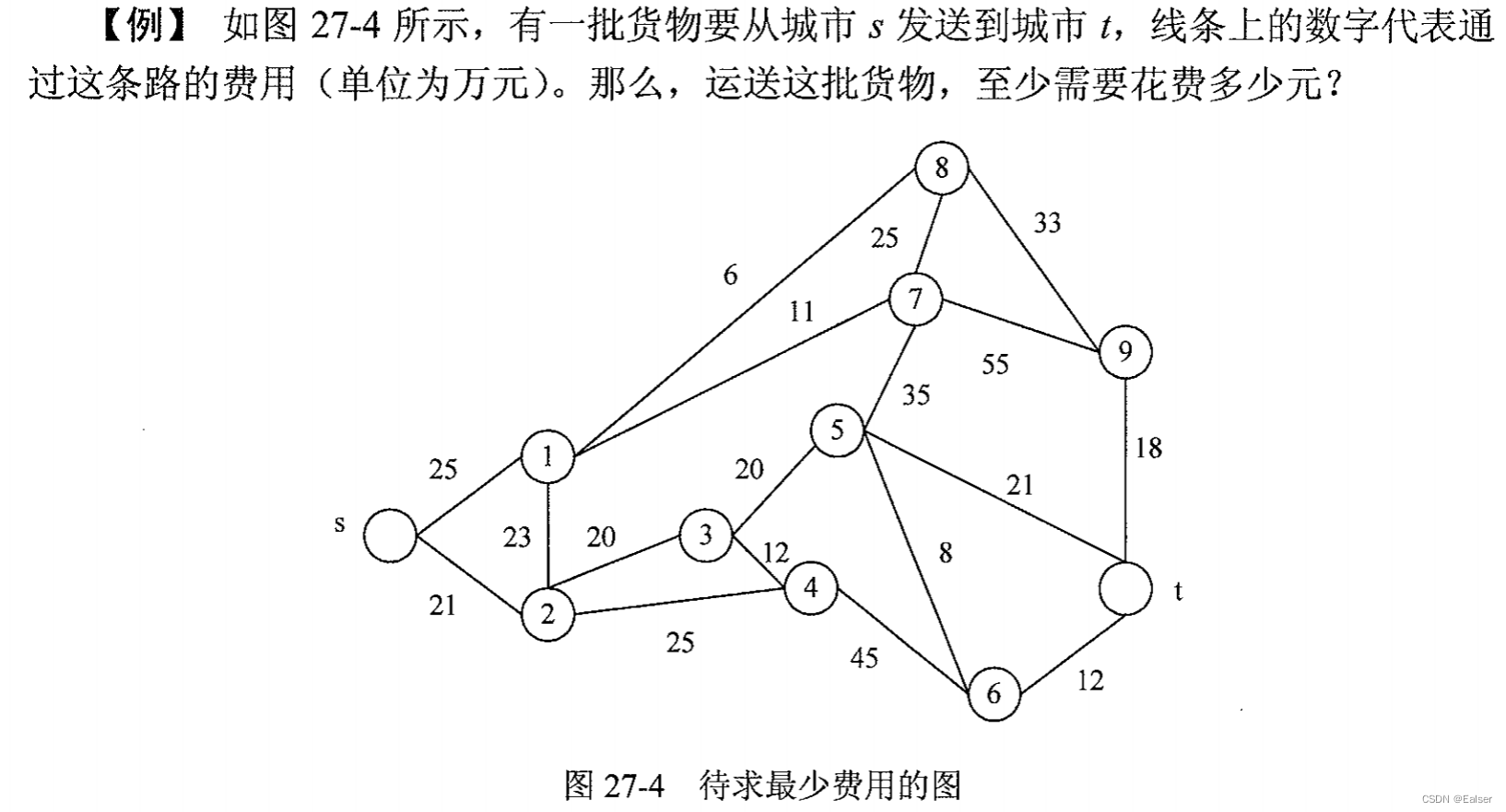
题4

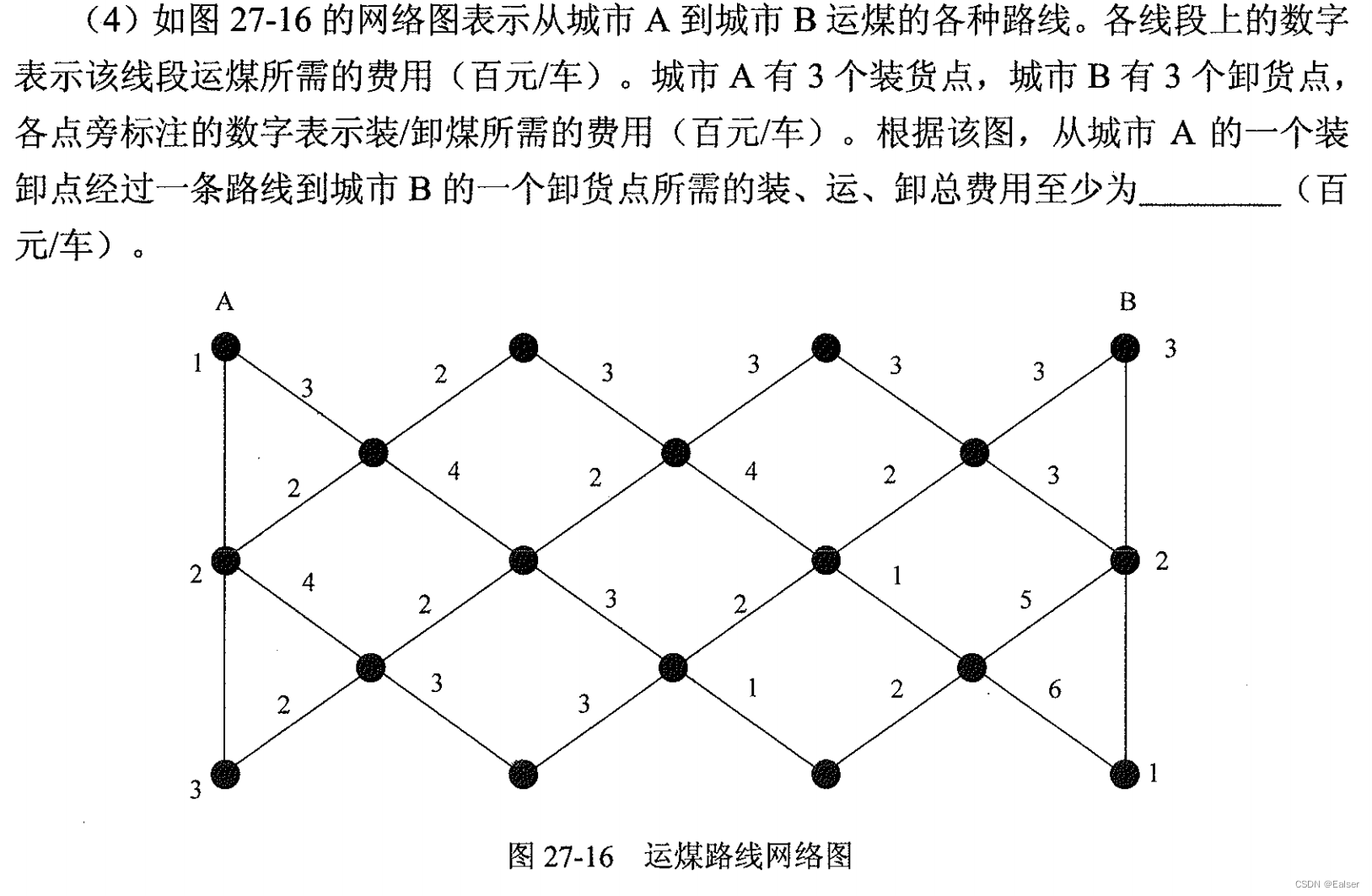
题5

【例14-18下】工程师小张需要完成图中所有区域的巡检工作，圈中圆圈代表巡检地点，两点之间的连接线为可行的交通路径，连接线为可行的交通路径，连接线上所标识的数字为两点之间所需的交通费用（单位:元），从地点1开始完成巡检（不需要按数字顺序也无需返回起点）所需的最少交通费为（）元。
A.392 B.450 C.400 D.470

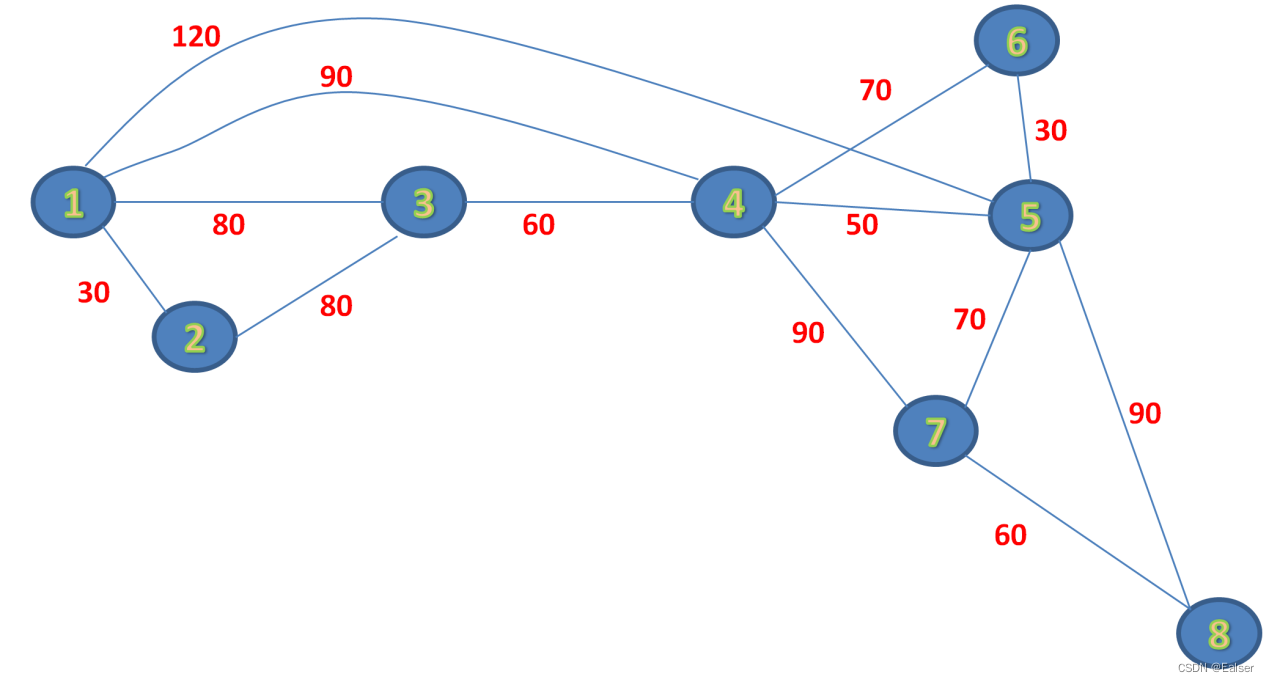
题6

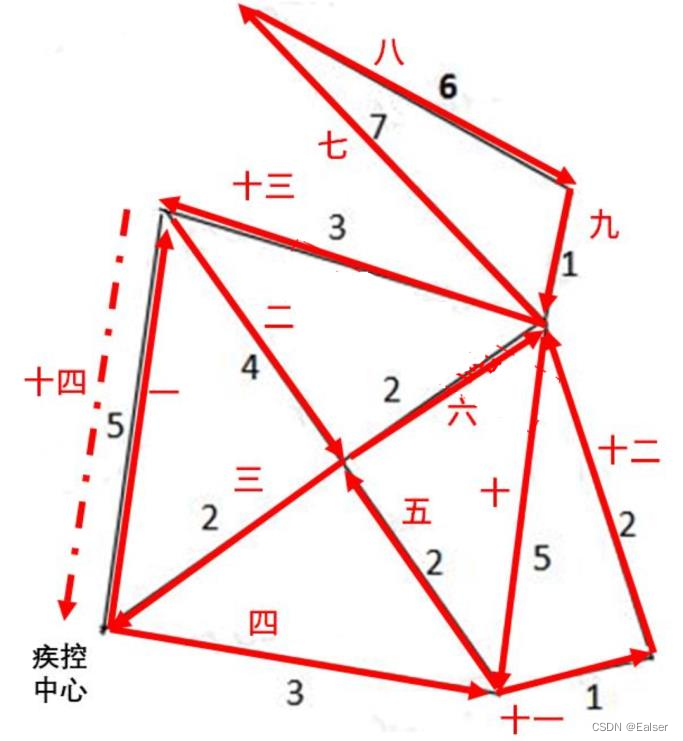
【例15-22上】下图是某地的街区网络图（单位：公里），疫情防控期间，一辆消毒车中心出发，需要消杀所有的街道并返回疾控中心，消杀车完成消杀工作至少需要运行（）公里。

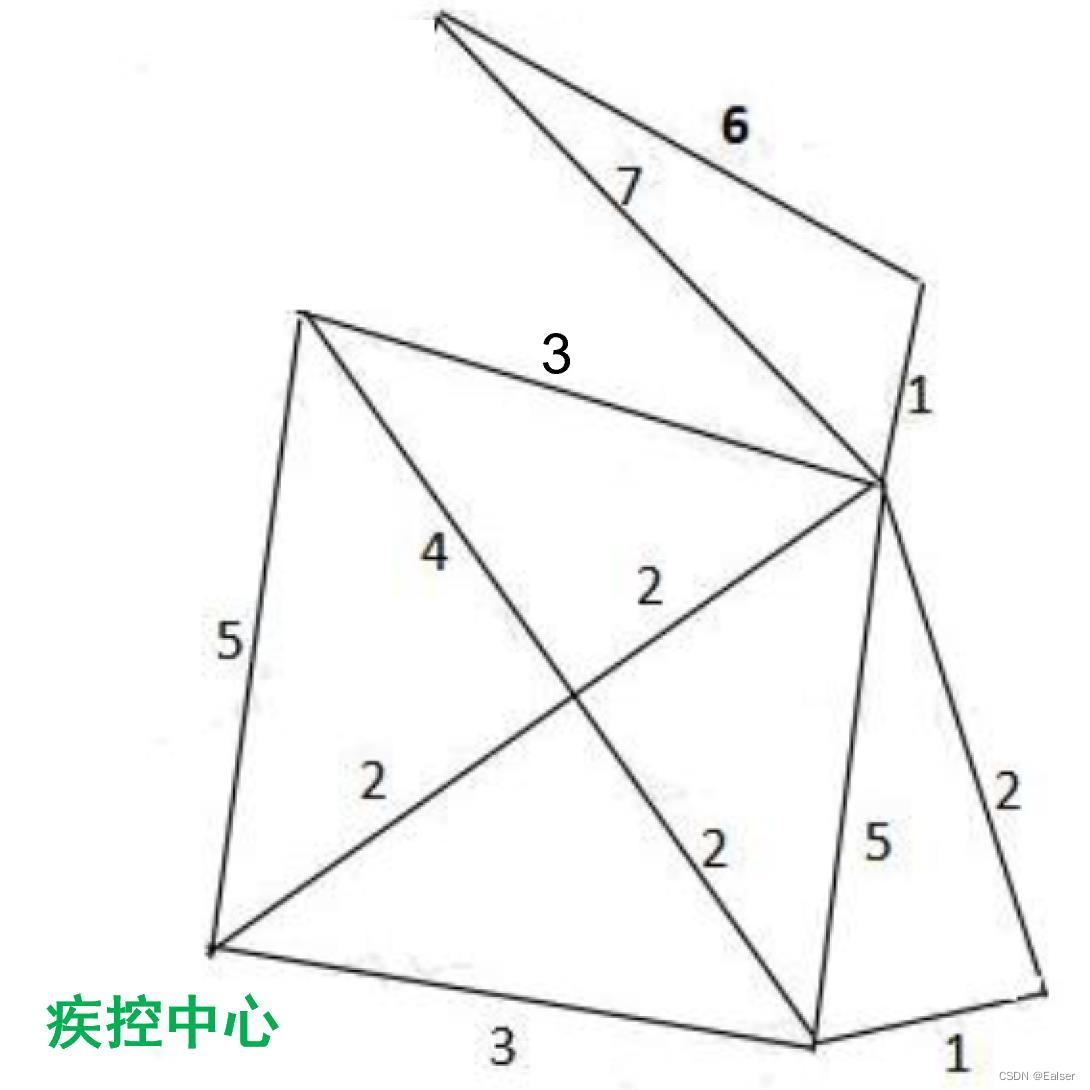
A.43 B.45 C.46 D.48
解答：

因为出发点（控制中心）的上面的相邻点也是奇数点，而出发点（控制中心）右边的相邻点是偶数点，基于（一笔画理论或者说是遍历理论）奇数点上不能所有线都只走一遍，必定有一点线会多走一次，偶数点可以所有线都只走一遍，所以出发点和出发点上面的点都是必须要多走一次的，多
走一次，那么就是所有线路先加起来，再加上多走一次的线路长度。思路是同一条路尽量不要往返，最好只走一次。先把全部路径的公里数算出来：（1+1）+（2+2+2+2）+（3+3）+4+（5+5）+6+7=43见图，大写数字为顺序，最后第十四步虚线这条路要多走一次，所以43+5=48大家可以多试试，可能不只一种走法，但应该至少都要48公里

题7

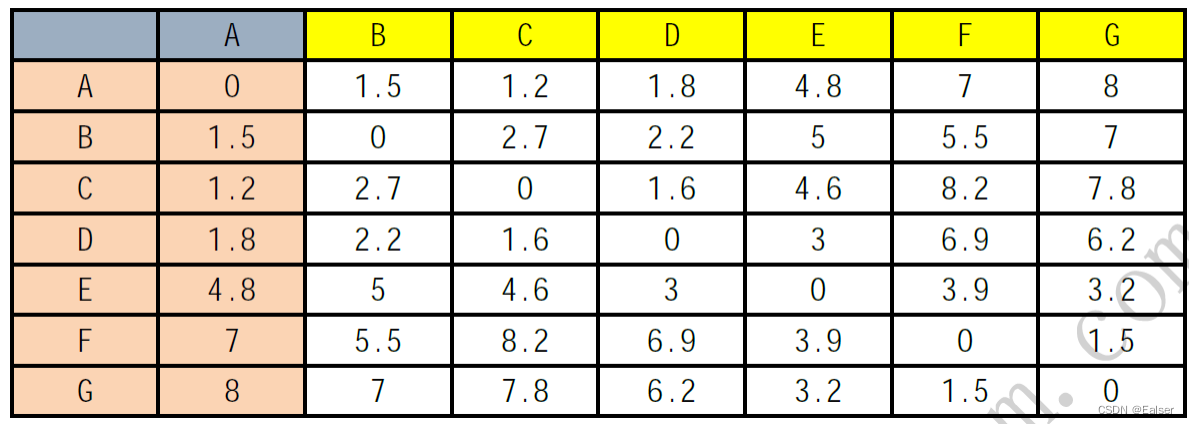
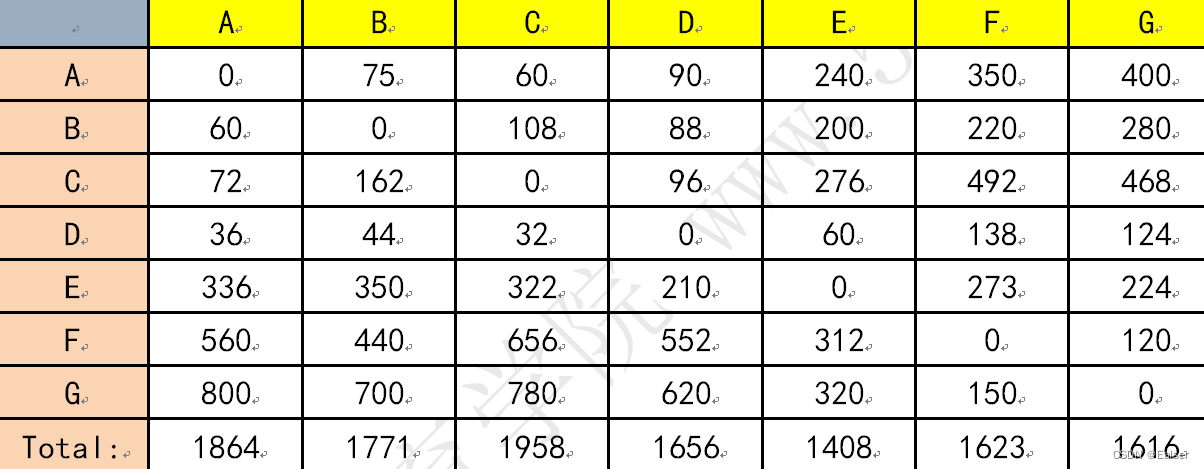
【例16-12下】 A、B、C、D、E、F、G代表七个村落，村落之间的道路连通情况如下图所示（边上的数据为距离，单位为公里）。这七个村落拟合建一所小学，已知A村有小学生50人、B村有小学生40人、C村有小学生60人、D村有小学生20人、E村有小学生70人、F村有小学生80、G村有小学生100人。则拟合建小学应建在（）村落，才能使学生上学所走的总路程最短。
A.C B.A C.F D.E

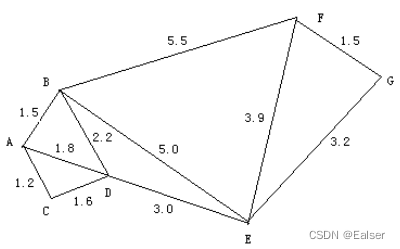
解法一:
题目为最短路径问题，可以将选项中的4个村的最短路径分别计算出来，进行比较即可:
在C村落的总路程为50x1.2+40x2.7+20x1.6+70x4.6+80x8.2+100x7.8=1958
在A村落的总路程为40x1.5+60x1.2+20x1.8+70x4.8+80x7+100x8=1864
在F村落的总路程为50x7+40x5.5+60x8.2+20x6.9+70x3.9+100x1.5=1623
在E村落的总路程为50x4.8+40x5+60x4.6+20x3+80x3.9+100x3.2=1408
在E村落的总路程最短。
此题如果时间不够计算，可以只计算E, F的路程。因为E, F村落人最多。相比来看，A, B, C, D距
离E更近。直接选择E

解法二:
首先得出一个到达矩阵如下 ，每一列代表一个学校可选的地方，第一行代表从A到这些地方的距离，第二行代表从B到所有的距离:

再用A的人数乘以这个矩阵第一行，B的人数乘以第二行，。。。得到如下:

8 最大流量问题

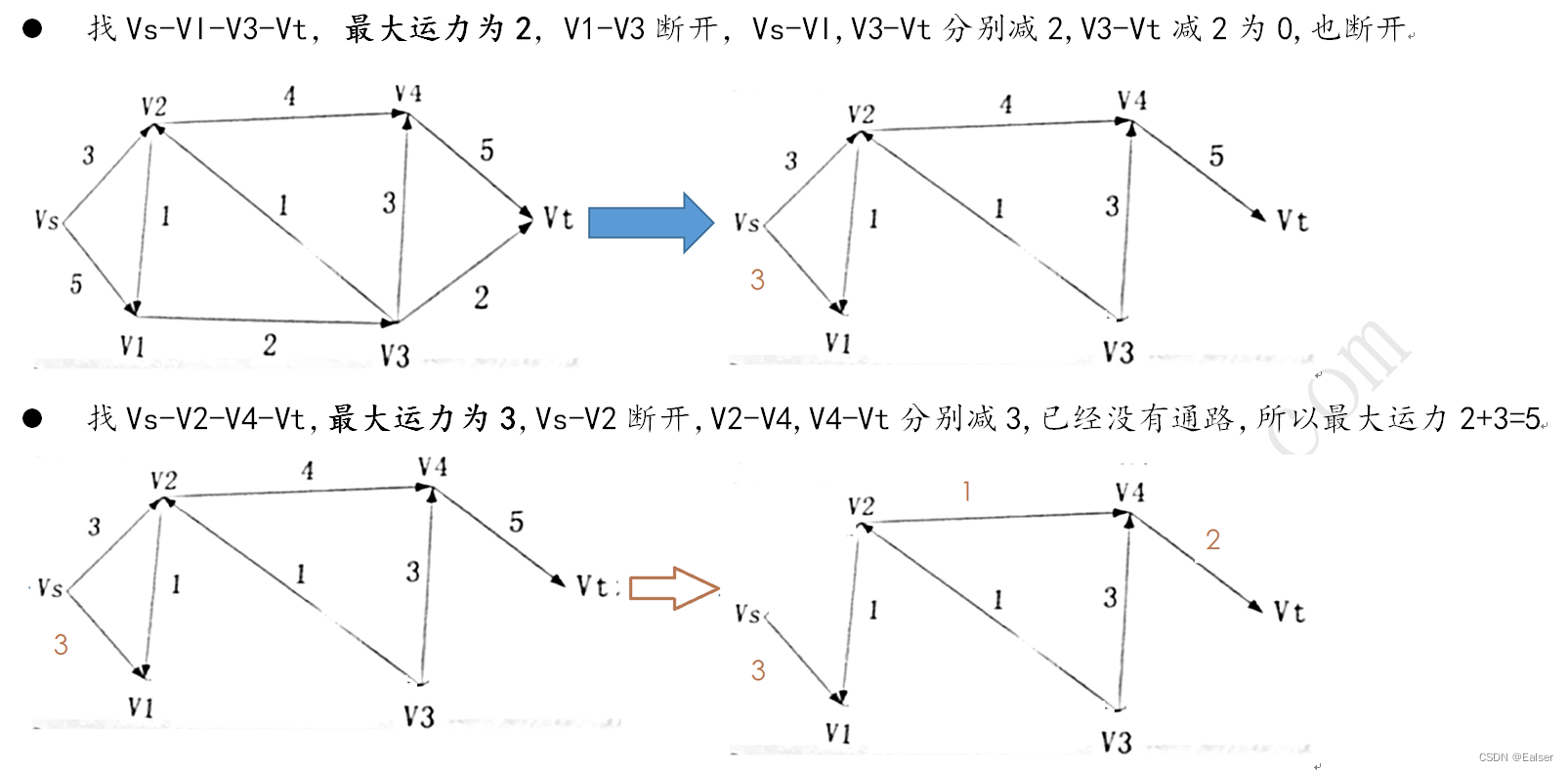
【例17-17上】下图标出了某产品从产地Vs到销地Vt的运输网，剪线上的数字表示这条输线的最大通过能力（流量）（单位:万吨/小时）。产品经过该运输网从Vs到Vt的最大运输能力可以达到（）万吨/小时。

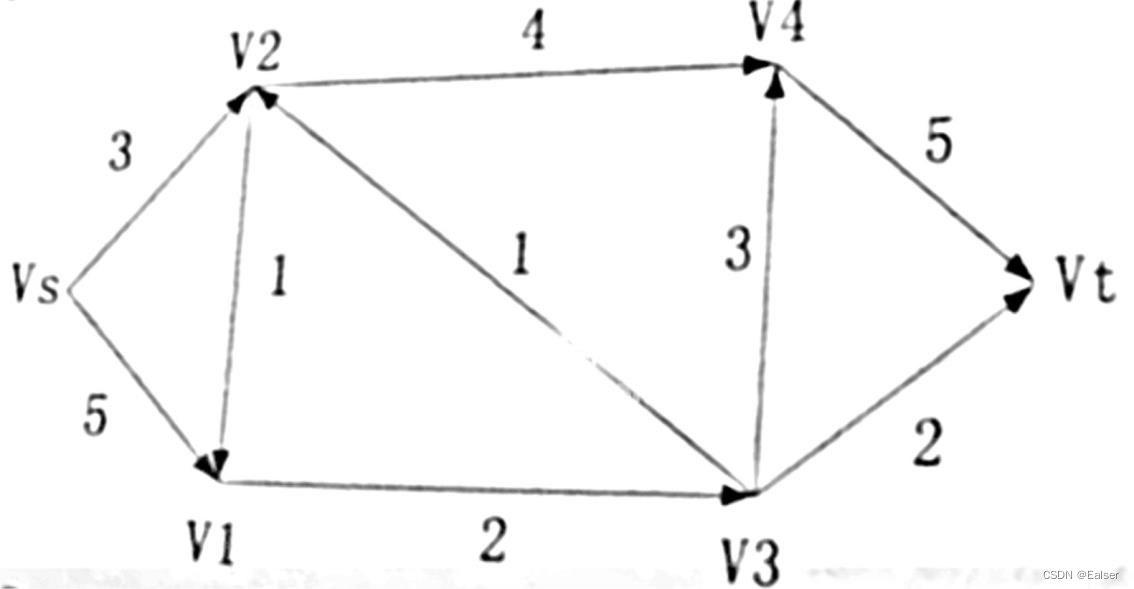
A.5 B.6 C.7 D.8

此题是求关键路径？？我想这是很多人的思路。不是
解题时，每找出一条路径算出流量后，该路径上各段线路上的流量应扣除已经算过的流量，形成剩余流量。剩余流量为0的线段应将其删除（断开）。这种做法比较简单直观。—教材P868类似

解答：

最大运输能力问题，参见2006年11月第63题，这个运筹学讲课里也有重点讲解。
解题时，找出每条路径中的流量瓶颈（路径中的最小流量值，如珠海到深圳要经过虎门大桥，不管前面的路有多宽，到虎门大桥后，由于虎门大桥流量只有10,所以这个10就是本路径的最大运力）。然后将其断开，路径上的其他运力减去该值。然后重复。过程见下图:

9 决策论 最大最小（max min）最小最大（min max）

✓最大最小（max min）:先取最小，然后取最大。步骤与意思相反 （对应题1）
✓最小最大（min max）:先取最大，然后取最小。步骤与意思相反 （对应2012.5 69 题）
1、乐观主义准则也称为最大最大准则(maxmax准则），其决策的原则是“大中取大”
2、悲观主义准则也称为最大最小准则(maxmin准则），其决策的原则是“小中取大”
3、后悔值准则也称为最小最大后悔值(minmax准则），每列最大值减去其他，算出最大后悔值，再从所有的最大值里面取最小值

题1

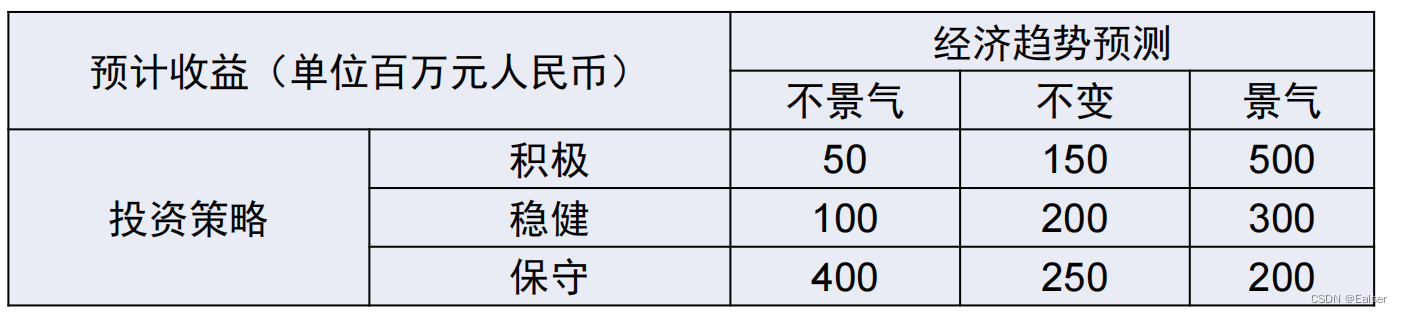
【例18-06下】某公司需要根据下一年度宏观经济的增长趋势预测决定投资策略。宏观经济增长趋势有不景气、不变和景气3种，投资策略有积极、稳健和保守3种，各种状态的收益如下表所示。基于max min 悲观准则的最佳决策是（）。教材P873-874

题2

【例19-12上】某企业开发了一种新产品，拟定的价格方案有三种:较高价.中等价.较低价，估计这种产品的销售状态也有三种:销路较好.销路一般.销路较差。根据以往的销售经验，他们算出。这三种价格方案在三种销路状态下的收益值如表3 所示:教材P883

企业一旦选择了某种决策方案，在同样的销路状态下，可能会产生后悔值（即所选决策方案产生的收益与最佳决策收益值的差值）。例如，如果选择较低价决策，在销路较好时，后悔值就为8万元。因此，可以根据上述收益值表制作后悔值如表4所示（空缺部分有待计算）:

企业做定价决策前，首先需要选择决策标准。该企业决定采用最小-最大后悔值决策标准（坏中求好的保守策略），为此，该企业应选择决策方案（）。
A.较高价 B.中等价 C.较低价 D.中等价或较低价

题3

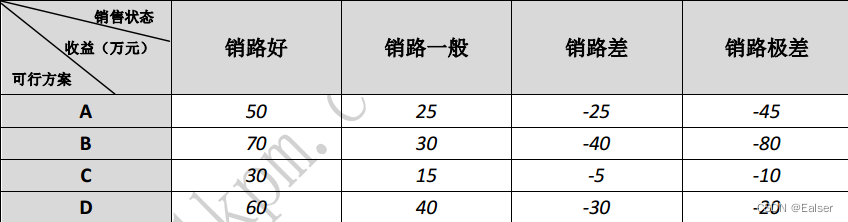
【例20-14下】三个备选投资方案的决策损益表如下，如果采用最大最小决策标准（悲观主义），则选择（）。教材P873-874

A.方案A B.方案B C.方案C D.方案D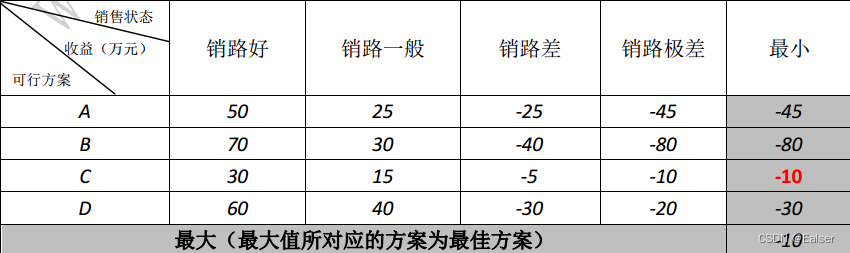

10 伏格尔法

伏格尔方法解传输运输学问题
伏格尔方法（Vogel） 主旨:最大差额处，优先按最小运价进行调运。
✓Vogel法的思想是:一地的产品如果不能按照最小运费就近供应，就考虑次小运费，这就有差额，差额越大，说明不能按最小运费调运时，运费增加得越多。因而差额越大处，就应当采用最小运费调运。
✓第一步:计算单位运价表中同行、同列的最小运费与次小运费之差，分别列在单位运价表的最右列和最下行（行差和列差）。
✓第二步:对行差和列差进行对比，找出最大差额。以与最大差额值同行（或同列）的最小运价为准，倾所在行的产量，最大限度地满足所在列的需求；一旦需求（或库存）被彻底满足（或库存调光），则随即划去该列（或行）的所有运价信息。（注意产量和销量的变化）
✓第三步:重新计算同行同列的最小运费与次小运费之差，并对其它未被确定调拨值的行列，重复第二步的处理，直至构造出调拨方案。
-----此种 方法很有技巧性，希望大家掌握，非常神奇的一种方法

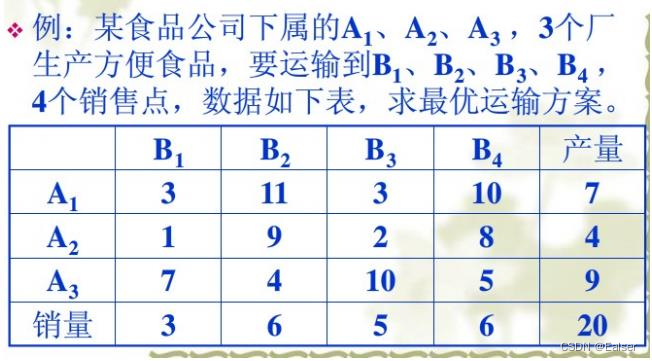
题1

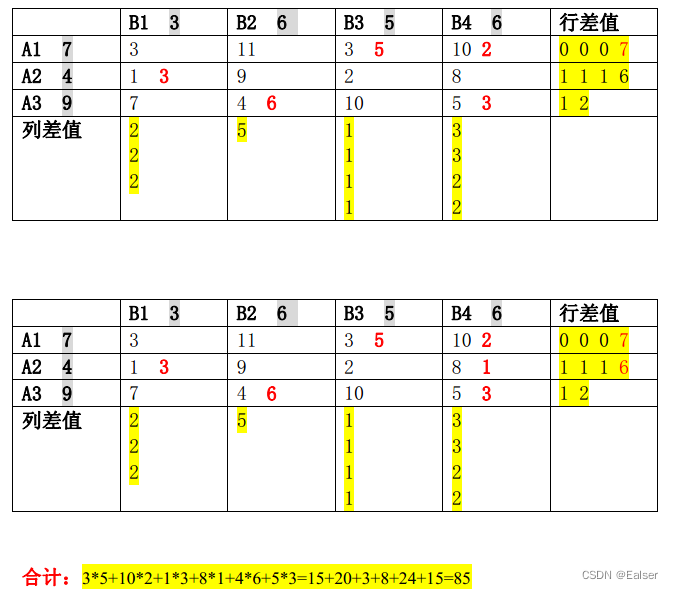
题2

【例21-12上】两家工厂A1 和A2 向三个零售店B1、B2和B3 供应某种商品。A1 和A2 可供应的商品件数是200 和300 ，而B1、B2 和B3 的需求量是100件200件和50件。各工厂和零售店之间可以进行转运。如果运输的单位成本如下所示（例如:表中第4列第3 行的数字“5”表示将一件商品从A2运到B1的成本）:

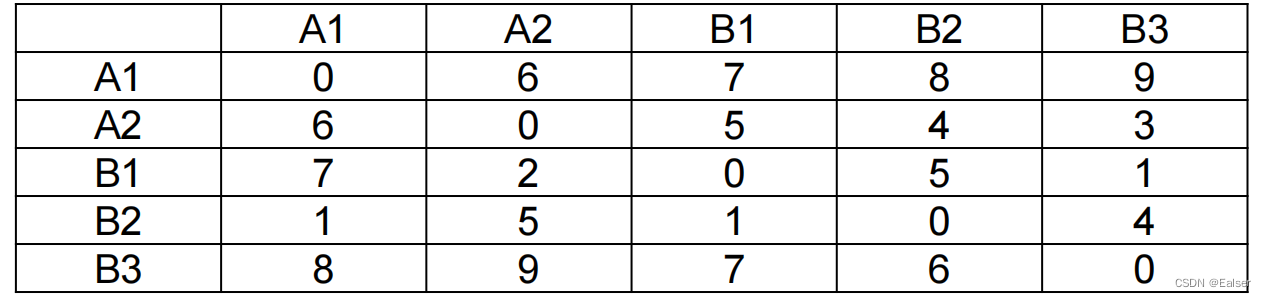
在最优的转运安排中，满足各零售商品需求的运输总成本是（）。
A.1750 B.1550 C.1350 D.850

题3

【例22-13上】某部门有3个生产同类产品的工厂（产地），生产的产品由4个销售点（销地）出售，各工厂的生产量（单位:吨）、各销售点的销售量（单位:吨）以及各工厂到各销售点的单位运价（百元/吨）示于表4中:

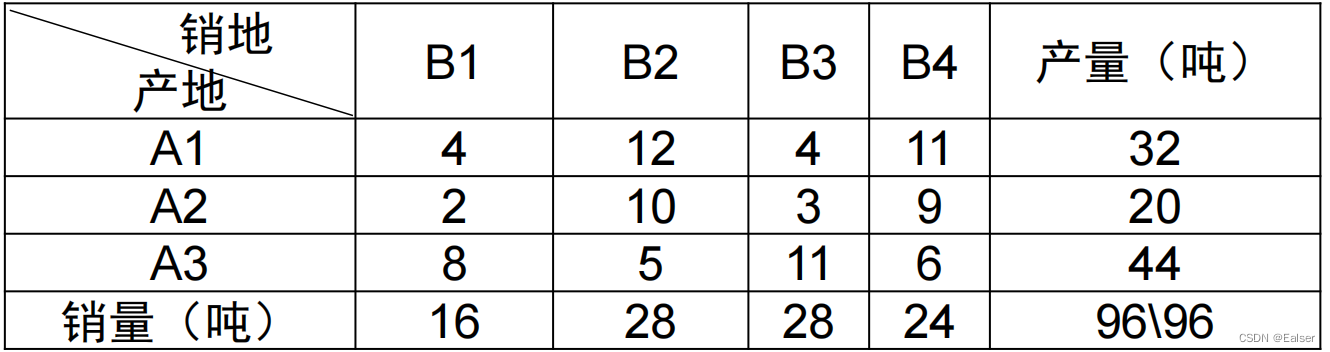
适当安排调运方案，最小总运费为（）。

A.450 B.455 C.460 D.465

题4

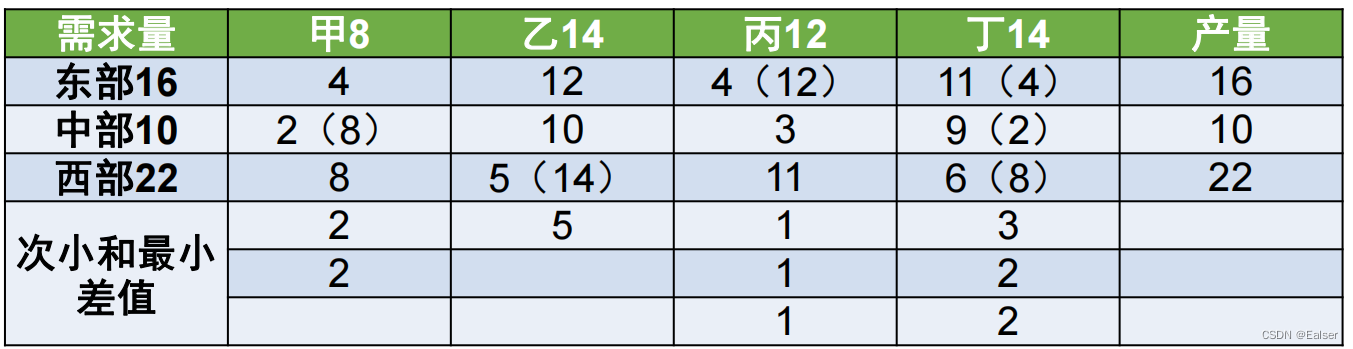
【例23-22上】某公司有东部、中部、西部三个生产基地，生产的产品需要运送带甲、乙、丙、丁四个市场，从生产基地到各个市场的单位运价及产量和需求量如表所示，完输任务所需的最小运费为（）。

A.242 B.244 C.289 D.302

11车床铣床问题

一个学员提出的解题思路:
就是有关车床和铣床的最短时间的命题:（以08高下69为例）
错误的做法是:不是要先找车床工序的最小值，再找铣床工序的最小值，再找车床工序的第二最小值，再找铣床工序的第二最小值。
纠正的结论是:先找第一最小值，第二最小值...依次如果是车床就从前到后、如果是铣床就从后到前排列。
下面以08高下69为例:先找第一最小值，如果是车床就放第一位，如果是铣床就放最后一位。此命题是2是铣床所以C是最后一位。
先找第二最小值，如果是车床就放第一位，如果是铣床就放倒数第二位。此命题是4是车床所以B是第一位。
再找第三最小值，如果是车床就放第二位，如果是铣床就放倒数第二位。此命题是5是铣床所以D是倒数第二位。
最后，剩余A是第二位。所以BADC。
在统计最小值时，已经排好顺序的零件的工时不在本次统计范围内。

11.1 题1

【例24-09下】某车间需要用一台车床和一台铣床加工A、B、C、D四个零件。每个零件都需要先用车床加工，再用铣床加工。车床与铣床加工每个零件所需的工时（包括加工前的准备时间以及加工后的处理时间）如下表:

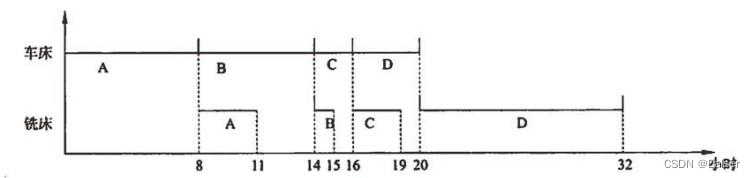
若以A、B、C、D零件顺序安排加工，则共需32小时。适当调整零件加工顺序，可使所需总工时最短。在这种最短总工时方案中，零件A在车床上的加工顺序安排在第（69）位，四个零件加工共需（70）小时。
（69）A.1 B.2 C.3 D.4
（70）A.21 B.22 C.23 D.24
这种题目的调整原则如下:

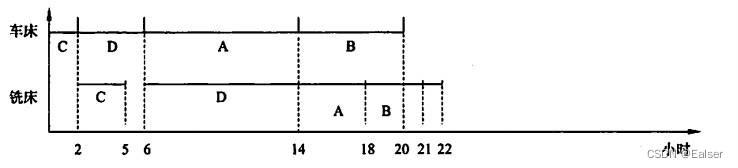
◆ 第一步:将车床耗时最短的活动放在车床工作的第一位；
◆ 第二步:将铣床耗时最短的活动放在铣床工作的倒数一位；
◆ 第三步:将剩下工作中车床耗时最短的活动放在车床工作的第二位；
◆ 第四步:将剩下工作中铣床耗时最短的活动放在铣床工作的倒数第二位；
以顺序安排加工A-B-C-D 4个零件为例，人们可以用甘特图将工作进度计划描述如下:

这样，最优方案应是按CDAB零件的顺序来加工，其甘特图如下:

11.1 题2

【例25-13下】某企业计划研发甲、乙、丙、丁四种产品。每种产品必须依次由设计部门、制造部门和检验部门进行设计、制造和检验，而每个部门必须按同样的顺序处理这几种产品。各种产品的各项工作所需的时间如下表所示。

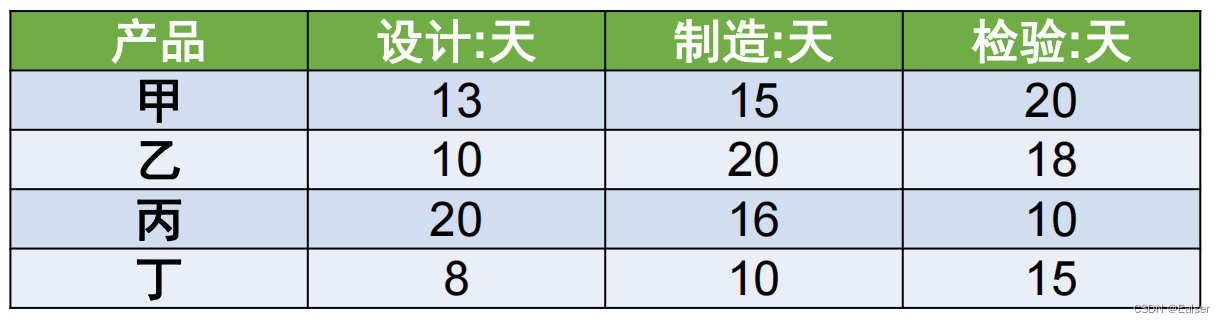
只要适当安排好产品研究的顺序，企业最快可以在（）天内全部完成这四种产品的研发。
A.84 B.86 C.91 D.93

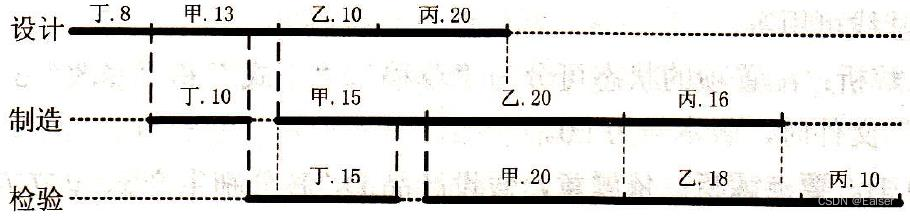
【解题思路】先找出第一道工序里面时间最短的排第一 ，再找出第二道工序里面时间最最短的排最后，然后再找次小的排第二，剩下的就排最后
每种产品必须依次经过设计、制造和检验3个环节，每个部门 按同样的顺序处理产品甲、乙、丙、丁。为了缩短项目总工时，应适当安排各产品的工作顺序，以缩短设计环节最先的工作时间（产品制造之前需要等待的时间），并缩短其检验环节最后的工作时间。因此应采取如下原则来安排各产品研发的工作顺序:在下所示的工时表中找出最小值，如 果它是设计时间，则其对应的产品应最先研发，如果它是检验时间;则其对应的产品应最后研发。 除去某最短设计时间的产品之后，再按此原则继续进行安排,如下图所示:

从如图所示的可以看出，该企业按照“丁、甲、乙、丙”的产品研发顺序，总共需要
8+13+15+20+18+10=84 天

12 设备更换问题

【例26-12上】一家公司需要确定使用期为5年的一种设备的更换策略。已知各年购买设备的价格和各年龄设备的维修价格如表5和表6所示:

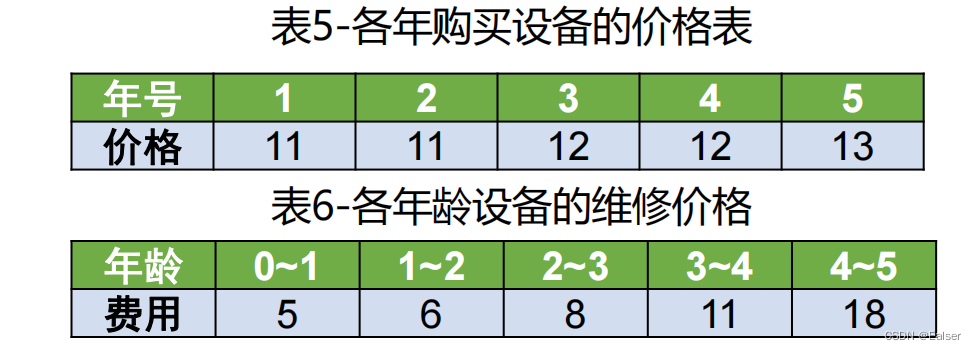
最优的设备更换策略中，总费用是（）。
A.50 B.53 C.59 D.71

13 换算方案问题

【例27-19下】为响应环保号召，某电池生产厂家承诺用3块旧电池可以换1块新电池，小李有21块旧电池，请问他一共可以换取（）新电池。
A.7 B.9 C.10 D.1

这题是埋坑了，如果是 21/3= 7 （选了A），就是踩坑了。
用21块旧电池，可以马上换7块新电池（+7）。但是，这7块新电池用完了，还可以换的，可以换 7/3 = 2块新电池（+2），还剩余一块旧电池。
2块新电池用完了，小李手里就又有了3块旧电池（外加之前剩余的一个旧电池），这样还可以换一块新电池（+1）。
这块新电池用完了，小李手上只有一块旧的电池，不够换一块新电池了。 所以:小李总共换了:7+2+1=10块电池。