一、整数规划
定义：数学规划中的变量（部分或全部）限制为整数时，称为整数规划。
若在线性规划模型中，变量限制为整数，则称为整数线性规划。
分类：（1）变量全部限制为整数时，称为纯（完全）整数规划；（2）变量部分限制为整数时，称为混合整数规划。
特点：
（1）原线性规划有最优解，当自变量限制为整数后，其整数规划解出现下述情况。
原线性规划最优解全是整数，则整数规划最优解与线性规划最优解一致
整数规划无可行解
有可行解（存在最优解），但最优解值变差
（2）整数规划最优解不能按照实数最优解简单取值而获得。
求解方法分类：
分枝定界法——可求完全或混合整数线性规划
割平面法——可求完全或混合整数线性规划
隐枚举法——求解“0－1”整数规划
匈牙利法——解决指派问题
蒙特卡洛法——求解各种类型规划
二、非线性规划的Matlab标准形式及问题求解

   

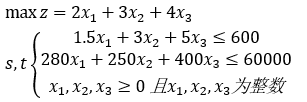
c=[2;3;4];
a=[1.5,3,5;280,250,400];
b=[600;60000];
intcon=[1,2,3];
[x,y]=intlinprog(-c,intcon,a,b,[],[],zeros(3,1))
x,y=-y

 

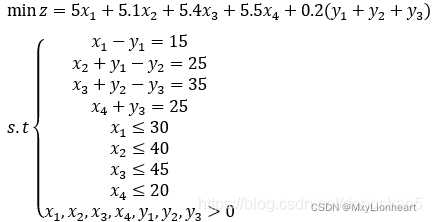
f=[5;5.1;5.4;5.5;0.2;0.2;0.2];
a=[1 0 0 0 0 0 0;0 1 0 0 0 0 0 ;0 0 1 0 0 0 0;0 0 0 1 0 0 0];
b=[30;40;45;20];
aeq=[1 0 0 0 -1 0 0;0 1 0 0 1 -1 0 ;0 0 1 0 0 1 -1;0 0 0 1 0 0 1];
beq=[15;25;35;25];
intcon=[1,2,3,4,5,6,7];
[x,y]=intlinprog(f,intcon,a,b,aeq,beq,zeros(7,1))

 四、整数非线性规划的代码实现（matlab）
max z = x(1)2+x(2)2+3x(3)2+4*x(4)2+2x(5)^2-8x(1)-2x(2)-3x(3)-x(4)-2x(5)
约束条件为：
x1 + x2 + x3 + x4 + x5 <= 400
x1 + 2x2 + 2x3 + x4 + 6x5 <= 800
2x1 + x2 + 6x3 <= 200
x3 + x4 + 5x5 <= 200
0=< xi <= 99 , i = 1,2,3,4,5

function myfun
x0 = [50 99 0 99 20];
A = [1,1,1,1,1;1,2,2,1,6;2,1,6,0,0;0,0,1,1,5];
b = [400,800,200,200];
Aeq = [];
beq = [];
VLB = [0;0;0;0;0];
VUB = [99;99;99;99;99];
[x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,VLB,VUB)
end

function ff = fun(x)
    ff = -(x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)^2-8*x(1)-2*x(2)-3*x(3)-x(4)-2*x(5));
end

五、蒙特卡罗法求解整数非线性规划
max z = x12+x22+3x32+4*x42+2x5^2-8x1-2x2-3x3-x4-2x5
约束条件为：
x1 + x2 + x3 + x4 + x5 <= 400
x1 + 2x2 + 2x3 + x4 + 6x5 <= 800
2x1 + x2 + 6x3 <= 200
x3 + x4 + 5x5 <= 200
0=< xi <= 99 , i = 1,2,3,4,5
 

% 主函数
rand('state',sum(clock));
p0=0;
tic
for i=1:100
   x1=randi([0,99],5,1);
   [f,g]=mengte(x1);
    if sum(g<=0)==4
       if p0<=f
          x0=x1;p0=f;
       end
    end
end
x0,p0
toc

function [f,g]=mengte(x);
f=x(1)^2+x(2)^2+3*x(3)^2+4*x(4)^2+2*x(5)-8*x(1)-2*x(2)-3*x(3)...
   -x(4)-2*x(5);
g(1)=sum(x)-400;
g(2)=x(1)+2*x(2)+2*x(3)+x(4)+6*x(5)-800;
g(3)=2*x(1)+x(2)+6*x(3)-200;
g(4)=x(3)+x(4)+5*x(5)-200;
end