一、策略网络的小结:
重要概念回顾:
1、动作价值函数QΠ(st,at)
动作价值函数是未来奖励总和Ut的条件期望,如果已知了策略函数Π与当前的状态st,QΠ就可以对所有的动作a打分,以此来决定选择哪个a
其实顾名思义就是给所有当前状态下所有动作打分的函数
2、状态价值函数VΠ(st)=EA[QΠ(st,A)],A~(·|st)
顾名思义就是给当前所处状态打分,得到一个值来判断当前状态是好是坏
1、策略学习的最终目标
》学习到一个策略函数Π,比如在当前状态下,agent需要做动作,但是它不知道应该做什么,就调用Π(a|s)函数,来决定当下最应该做出什么动作
在这里,调用Π(a|s)函数会得到一个数组(0.2,0.1,0.7),数组里的每个元素代表相应动作被选择的概率,然后agent从里面随机抽一个动作来执行
2、但是现实中可能有无数个状态/动作,而且我们无法预知未来,得到这个上帝函数Π(绝对正确),那么应该怎么办呢?
》使用策略神经网络Π(a|s;θ)来近似Π(a|s),所以我们的目标就是学习到一个最好的神经网络参数θ,来使Π(a|s;θ)无限接近Π(a|s)
3、我如何评价神经网络参数θ的好坏呢?
》使用V(st;θ)=。。。。。。。。。。。。来评价策略网络Π(a|s;θ)的好坏,进而评价θ的好坏,我们可以通过求V(st;θ)的极大值来获得局部最大值,也可以通过求V(st;θ)的条件期望J(θ)=ES[(S,θ)]来获得全局最大值,在本文的线性模型当中,求V(st;θ)的极大值就是全局的最大值了
4、那么如何求V(st;θ) max呢?
》先随机初始化参数θ,然后通过梯度上升,使得θ朝着极大值点的方向移动
5、如何求策略梯度
 呢?
呢?

1)假如动作是离散的,即A={"left","right","up"}
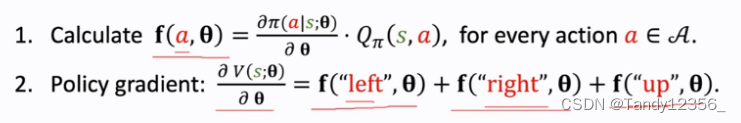
这样我们计算出来策略梯度,就可以更新参数θ了
2)假如动作是连续的,我们使用蒙特卡洛近似:

由于:![]()
所以:![]()
因此我们可以使用g(a hat,θ)来代替策略梯度
最后还有一个问题就是QΠ怎么算?
》
我们不知道QΠ,所以没法算qt,那么如何近似去算qt呢?
法一:用策略网络Π来控制agent运动,从一开始一直玩到游戏结束,把整个游戏的轨迹都记录下来,s1,a1,r1,s2,a2,r2,...sn,an,rn,观测到所有奖励r,我们就可以算出ut
由于价值函数QΠ是Ut的期望,我们可以用大Ut的观测值小ut来近似QΠ,所以reinforce强化算法就是使用观测到的ut来代替QΠ函数,reinforce算法需要玩完一局游戏,观测到所有的奖励,然后才能更新策略网络

法二:用一个神经网络来做近似:
原本已经用神经网络近似了策略函数Π,现在用另一个神经网络来近似价值函数QΠ,这样就有了两个神经网络,一个被称为Actor,一个被称为Critic,这样就有了actor-critic方法
总结一下策略梯度算法:
1、在第t个时间点,观测到了状态st
2、使用蒙特卡洛近似来计算策略梯度,把策略网络Π作为概率密度函数,用它随机抽样得到一个动作at,比如at是向左的动作
3、计算价值函数QΠ的值,把结果记作qt
4、对策略网络Π求导,算出logΠ关于θ的导数,得到的结果dθ,t是向量、矩阵或者是张量,dθ,t的大小和θ是一样的,如果θ是100*100的矩阵,那么dθ,t也是100*100的矩阵,tensorflow和pytorch这些系统都支持自动求梯度你告诉系统当前at,st还有当前参数θt,系统可以自动求出来梯度dθ,t
5、近似地计算策略梯度,用一个样本a来算策略梯度的蒙特卡洛近似
6、最后一步,有了近似的策略梯度,就可以用它来更新策略网络的参数θ了
二、价值网络小结:
写技术类的文章好烦,研究的人不多,没怎么有人看,如果没人互动的话,就不更新了,Tandy Monkey只能自我提升了。。。。。。。。。。。。。。。