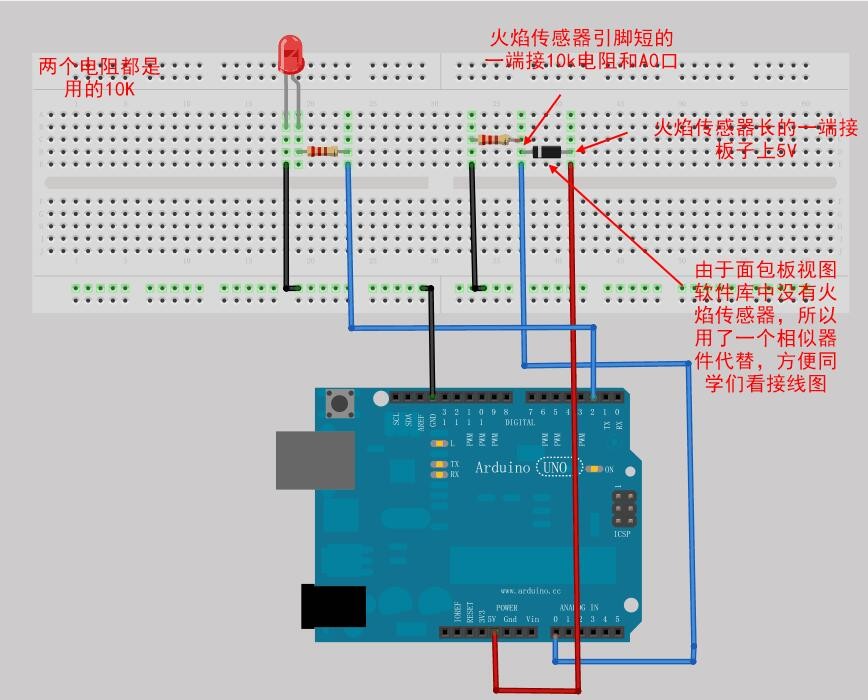
省一了,占个坑,今天晚上来补蓝桥的题
试题 A: 幸运数
本题总分:5 分
【问题描述】
小蓝认为如果一个数含有偶数个数位,并且前面一半的数位之和等于后面
一半的数位之和,则这个数是他的幸运数字。例如
2314
是一个幸运数字,因为
它有
4
个数位,并且
2 + 3 = 1 + 4
。现在请你帮他计算从
1
至
100000000
之间
共有多少个不同的幸运数字。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 B: 有奖问答
本题总分:5 分
【问题描述】
小蓝正在参与一个现场问答的节目。活动中一共有
30
道题目,每题只有答
对和答错两种情况,每答对一题得
10
分,答错一题分数归零。
小蓝可以在任意时刻结束答题并获得目前分数对应的奖项,之后不能再答
任何题目。最高奖项需要
100
分,所以到达
100
分时小蓝会直接停止答题。
已知小蓝最终实际获得了
70
分对应的奖项,请问小蓝所有可能的答题情况
有多少种?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一
个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
试题 C: 平方差
时间限制
: 1.0s
内存限制
: 256.0MB
本题总分:10 分
【问题描述】
给定
L
,
R
,问
L
≤
x
≤
R
中有多少个数
x
满足存在整数
y
,
z
使得
x
=
y
2
−
z
2
。
【输入格式】
输入一行包含两个整数 L, R,用一个空格分隔。
【输出格式】
输出一行包含一个整数满足题目给定条件的 x 的数量。
【样例输入】
1 5
【样例输出】
4
【样例说明】
1 = 1
2
−
0
2
;
3 = 2
2
−
1
2
;
4 = 2
2
−
0
2
;
5 = 32 − 2 2 。
【评测用例规模与约定】
对于
40
%
的评测用例,
L R
≤
5000
;
对于所有评测用例,
1
≤
L
≤
R
≤
10
9
。
试题 D: 更小的数
时间限制
: 1.0s
内存限制
: 256.0MB
本题总分:10 分
【问题描述】
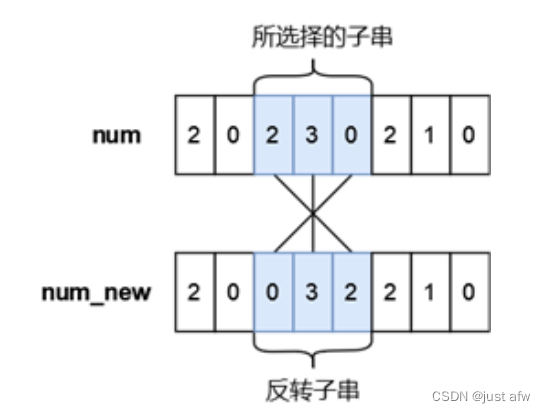
小蓝有一个长度均为 n 且仅由数字字符 0 ∼ 9 组成的字符串,下标从 0 到 n − 1,你可以将其视作是一个具有 n 位的十进制数字 num,小蓝可以从 num 中 选出一段连续的子串并将子串进行反转,最多反转一次。
小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 numnew 满足条件 numnew < num, 请你帮他计算下一共有多少种不同的子串选择方案,只要两个子串在 num 中的 位置不完全相同我们就视作是不同的方案。
注意,我们允许前导零的存在,即数字的最高位可以是 0 ,这是合法的。
【输入格式】
输入一行包含一个长度为
n
的字符串表示
num
(仅包含数字字符
0
∼
9
),
从左至右下标依次为 0 ∼ n − 1。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
210102
【样例输出】
8
【样例说明】
一共有 8 种不同的方案:
1
)所选择的子串下标为
0
∼
1
,反转后的
num
new
= 120102
<
210102
;
2
)所选择的子串下标为
0
∼
2
,反转后的
num
new
= 012102
<
210102
;
3
)所选择的子串下标为
0
∼
3
,反转后的
num
new
= 101202
<
210102
;
4
)所选择的子串下标为
0
∼
4
,反转后的
num
new
= 010122
<
210102
;
5
)所选择的子串下标为
0
∼
5
,反转后的
num
new
= 201012
<
210102
;
6
)所选择的子串下标为
1
∼
2
,反转后的
num
new
= 201102
<
210102
;
7
)所选择的子串下标为
1
∼
4
,反转后的
num
new
= 201012
<
210102
;
8)所选择的子串下标为 3 ∼ 4 ,反转后的 numnew = 210012 < 210102 ;
【评测用例规模与约定】
对于
20
%
的评测用例,
1
≤
n
≤
100
;
对于
40
%
的评测用例,
1
≤
n
≤
1000
;
对于所有评测用例,
1
≤
n
≤
5000
。
试题 E: 颜色平衡树
时间限制
: 1.0s
内存限制
: 256.0MB
本题总分:15 分
【问题描述】
给定一棵树,结点由
1
至
n
编号,其中结点
1
是树根。树的每个点有一个
颜色
C
i
。
如果一棵树中存在的每种颜色的结点个数都相同,则我们称它是一棵颜色
平衡树。
求出这棵树中有多少个子树是颜色平衡树。
【输入格式】
输入的第一行包含一个整数
n
,表示树的结点数。
接下来
n
行,每行包含两个整数
C
i
,
F
i
,用一个空格分隔,表示第
i
个结点
的颜色和父亲结点编号。
特别地,输入数据保证
F
1
为
0
,也即
1
号点没有父亲结点。保证输入数
据是一棵树。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
6
2 0
2 1
1 2
3 3
3 4
1 4
【样例输出】
4
【样例说明】
编号为 1, 3, 5, 6 的 4 个结点对应的子树为颜色平衡树。
【评测用例规模与约定】
对于
30
%
的评测用例,
n
≤
200
,
C
i
≤
200
;
对于
60
%
的评测用例,
n
≤
5000
,
C
i
≤
5000
;
对于所有评测用例,
1
≤
n
≤
200000
,
1
≤
C
i
≤
200000
,
0
≤
F
i
<
i
。
试题 F: 买瓜
时间限制
: 1.0s
内存限制
: 256.0MB
本题总分:15 分
【问题描述】
小蓝正在一个瓜摊上买瓜。瓜摊上共有
n
个瓜,每个瓜的重量为
A
i
。
小蓝刀功了得,他可以把任何瓜劈成完全等重的两份,不过每个瓜只能劈
一刀。
小蓝希望买到的瓜的重量的和恰好为
m
。
请问小蓝至少要劈多少个瓜才能买到重量恰好为
m
的瓜。如果无论怎样小
蓝都无法得到总重恰好为 m 的瓜,请输出 −1 。
【输入格式】
输入的第一行包含两个整数
n
,
m
,用一个空格分隔,分别表示瓜的个数和
小蓝想买到的瓜的总重量。
第二行包含
n
个整数
A
i
,相邻整数之间使用一个空格分隔,分别表示每个
瓜的重量。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
3 10
1 3 13
【样例输出】
2
【评测用例规模与约定】
对于
20
%
的评测用例,
n ≤ 10 ;
对于
60
%
的评测用例,
n ≤ 20 ;
对于所有评测用例,
1
≤
n ≤ 30,1 ≤ A
i
≤
10
9
,
1
≤
m
≤
10
9
。
试题 G: 网络稳定性
时间限制
: 1.5s
内存限制
: 256.0MB
本题总分:20 分
【问题描述】
有一个局域网,由
n
个设备和
m
条物理连接组成,第
i
条连接的稳定性为
w
i
。
对于从设备
A
到设备
B
的一条经过了若干个物理连接的路径,我们记这条
路径的稳定性为其经过所有连接中稳定性最低的那个。
我们记设备
A
到设备
B
之间通信的稳定性为
A
至
B
的所有可行路径的稳
定性中最高的那一条。
给定局域网中的设备的物理连接情况,求出若干组设备
x
i
和
y
i
之间的通信
稳定性。如果两台设备之间不存在任何路径,请输出 −1 。
【输入格式】
输入的第一行包含三个整数
n
,
m
,
q
,分别表示设备数、物理连接数和询问
数。
接下来
m
行,每行包含三个整数
u
i
,
v
i
,
w
i
,分别表示
u
i
和
v
i
之间有一条稳
定性为
w
i
的物理连接。
接下来
q
行,每行包含两个整数
x
i
,
y
i
,表示查询
x
i
和
y
i
之间的通信稳定
性。
【输出格式】
输出 q 行,每行包含一个整数依次表示每个询问的答案。
【样例输入】
5 4 3
1 2 5
2 3 6
3 4 1
1 4 3
1 5
2 4
1 3
【样例输出】
-1
3
5
【评测用例规模与约定】
对于
30
%
的评测用例,
n
,
q
≤
500
,
m
≤
1000
;
对于
60
%
的评测用例,
n
,
q
≤
5000
,
m
≤
10000
;
对于所有评测用例,
2
≤
n
,
q
≤
10
5
,
1
≤
m
≤
3
×
10
5
,
1
≤
u
i
,
v
i
,
x
i
,
y
i
≤
n
,
1
≤
w
i
≤
10
6
,
u
i
,
v
i
,
x
i
,
y
i
。
试题 H: 异或和之和
时间限制
: 1.0s
内存限制
: 256.0MB
本题总分:20 分
【问题描述】
给定一个数组
A
i
,分别求其每个子段的异或和,并求出它们的和。或者说,
对于每组满足
1
≤
L
≤
R
≤
n
的
L
,
R
,求出数组中第
L
至第
R
个元素的异或和。
然后输出每组 L, R 得到的结果加起来的值。
【输入格式】
输入的第一行包含一个整数
n
。
第二行包含
n
个整数
A
i
,相邻整数之间使用一个空格分隔。
【输出格式】
输出一行包含一个整数表示答案。
【样例输入】
5
1 2 3 4 5
【样例输出】
39
【评测用例规模与约定】
对于
30
%
的评测用例,
n
≤
300
;
对于
60
%
的评测用例,
n
≤
5000
;
对于所有评测用例,
1
≤
n
≤
10
5
,
0
≤
A
i
≤
2
20
。
试题 I: 像素放置
时间限制
: 1.0s
内存限制
: 256.0MB
本题总分:25 分
【问题描述】
小蓝最近迷上了一款名为《像素放置》的游戏,游戏在一个
n
×
m
的网格
棋盘上进行,棋盘含有
n
行,每行包含
m
个方格。玩家的任务就是需要对这
n
×
m
个方格进行像素填充,填充颜色只有黑色或白色两种。有些方格中会出现
一个整数数字
x
(0
≤
x
≤
9)
,这表示当前方格加上周围八个方向上相邻的方格
(分别是上方、下方、左方、右方、左上方、右上方、左下方、右下方)共九个
方格内有且仅有
x
个方格需要用黑色填充。
玩家需要在满足所有数字约束下对网格进行像素填充,请你帮助小蓝来完
成。题目保证所有数据都有解并且解是唯一的。
【输入格式】
输入的第一行包含两个整数
n
,
m
,用一个空格分隔,表示棋盘大小。
接下来
n
行,每行包含
m
个字符,表示棋盘布局。字符可能是数字
0
∼
9
,
这表示网格上的数字;字符还有可能是下划线(
ASCII
码为
95
),表示一个不
带有数字的普通网格。
【输出格式】
输出
n
行,每行包含
m
个字符,表示答案。如果网格填充白色则用字符
0
表示,如果网格填充黑色则用字符
1
表示。
【样例输入】
6 8
_1__5_1_
1_4__42_
3__6__5_
___56___
_688___4
_____6__
【样例输出】
00011000
00111100
01000010
11111111
01011110
01111110
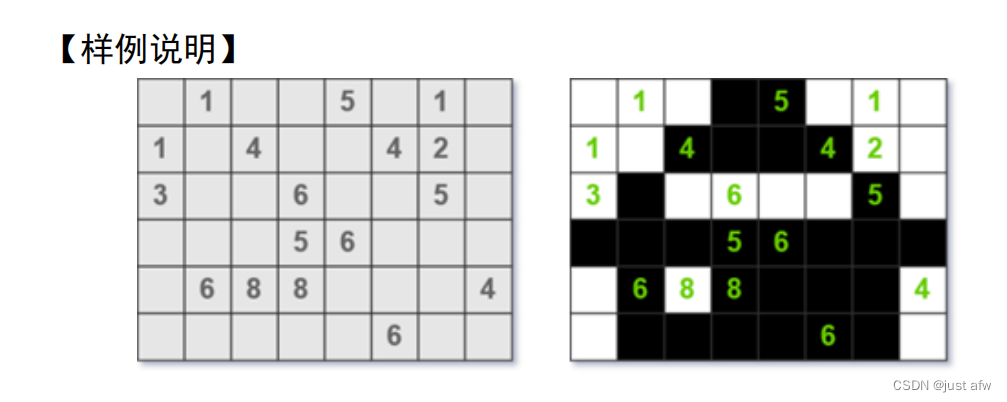
上图左是样例数据对应的棋盘布局,上图右是此局游戏的解。例如第
3
行
第
1
列处的方格中有一个数字
3
,它周围有且仅有
3
个格子被黑色填充,分别
是第 3 行第 2 列、第 4 行第 1 列和第 4 行第 2 列的方格。
【评测用例规模与约定】
对于
50
%
的评测用例,
1
≤
n
,
m
≤
5
;
对于所有评测用例,
1
≤
n
,
m
≤
10
。
试题 J: 翻转硬币
时间限制
: 3.0s
内存限制
: 256.0MB
本题总分:
25
分
【问题描述】
给定
n
个按顺序摆好的硬币,一开始只有第
1
个硬币朝下,其他硬币均朝
上。你每次操作可以选择任何一个整数
i
并将所有满足
j
mod
i
= 0
的位置
j
的
硬币翻转。
求最少需要多少次操作可以让所有硬币都朝上。
【输入格式】
输入一行包含一个整数
n
。
【输出格式】
输出一行包含一个整数表示最少需要的操作次数。
【样例输入
1
】
7
【样例输出
1
】
6
【样例输入
2
】
1131796
【样例输出
2
】
688042
【评测用例规模与约定】
对于
30
%
的评测用例,
n
≤
5
×
10
6
;
试题
J:
翻转硬币
16
第十四届蓝桥杯大赛软件赛省赛
C/C++
大学
A
组
对于
70
%
的评测用例,
n
≤
10
9
;
对于所有评测用例,
1
≤
n
≤
10
18
。