一开始看题解把我CPU干烧了

后来豁然开朗

E - Prefix Equality (atcoder.jp)

题意：

给定两个数组a,b，每次询问两个位置x和y，问a数组前x个构成的集合和b数组前y个构成的集合是不是一样

思路：

一开始纯暴力RE了

#include <bits/stdc++.h>

using namespace std;

const int mxn=2e5+10;
const int mxe=2e5+10;

set<int> S1[mxn],S2[mxn];

int N,Q,x,y;
int a[mxn],b[mxn];

signed main(){
	cin>>N;
	for(int i=1;i<=N;i++) cin>>a[i];
	for(int i=1;i<=N;i++) cin>>b[i];
	S1[1].insert(a[1]);
	S2[1].insert(b[1]);
	for(int i=2;i<=N;i++){
		S1[i]=S1[i-1];
		S1[i].insert(a[i]);
	}
	for(int i=2;i<=N;i++){
		S2[i]=S2[i-1];
		S2[i].insert(b[i]);
	} 
	cin>>Q;
	while(Q--){
		cin>>x>>y;
		if(S1[x]==S2[y]) cout<<"Yes"<<'\n';
		else cout<<"No"<<'\n';
	}	
}

 正解需要转化一下条件

（当没有思路的时候，关注题目的特殊条件和转化一下题目给的一般条件，这里没有特殊性质就去转化给定的一般条件）

它说a数组前x个构成的集合和b数组前y个构成的集合要一样

等效一下就是

a数组中1~x这些元素在b数组中出现的最晚位置要<=y

且

b数组中1~y这些元素在a数组中出现的最晚位置要<=x

因此DS的部分就来了！

我们需要维护两个东西：

a数组中1~x这些元素在b数组中出现的最晚位置

和

b数组中1~y这些元素在a数组中出现的最晚位置

那么怎么维护呢，我们去考虑修改部分

虽然这道题没有明显的修改操作，但是在遍历1~x的时候，每新加一个a[i] or b[i]，就相当于是“修改”操作（这是常见的套路）

考虑新加了一个a[i]，对“b数组中1~y这些元素在a数组中出现的最晚位置”会产生什么影响呢？

考虑转移

设pre_a数组为b[i]在a数组中出现的最晚位置，在遍历过程中维护这个数组

这里有点小小的贪心，我们希望出现的最晚位置尽可能前面，因此去维护一个数x在a数组中出现的最早位置，这样就能按以下转移：

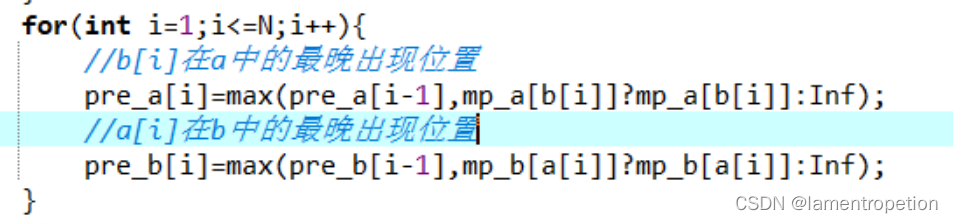
如果说x在数组中没出现过，那么在该数组中出现的最晚位置就是Inf

然后这道题就做完了

感觉很帅啊

Code：

#include <bits/stdc++.h>

#define int long long

using namespace std;

const int mxn=2e5+10; 
const int Inf=1e18;

map<int,int> mp_a,mp_b;

int N,Q,x,y;
int a[mxn],b[mxn];
int pre_a[mxn],pre_b[mxn];

signed main(){
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	cin>>N;
	for(int i=1;i<=N;i++) cin>>a[i];
	for(int i=1;i<=N;i++) cin>>b[i];
	for(int i=1;i<=N;i++){
		if(!mp_a[a[i]]) mp_a[a[i]]=i;
		if(!mp_b[b[i]]) mp_b[b[i]]=i;
	}
	for(int i=1;i<=N;i++){
		//b[i]在a中的最晚出现位置 
		pre_a[i]=max(pre_a[i-1],mp_a[b[i]]?mp_a[b[i]]:Inf);
		//a[i]在b中的最晚出现位置
		pre_b[i]=max(pre_b[i-1],mp_b[a[i]]?mp_b[a[i]]:Inf); 
	}
	cin>>Q;
	while(Q--){
		cin>>x>>y;
		if(pre_b[x]<=y&&pre_a[y]<=x) cout<<"Yes"<<'\n';
		else cout<<"No"<<'\n';
	}
}