文章目录

二叉树链式结构实现
- 1. 链式二叉树结构
- 2. 二叉树的遍历
- - 2.1 前序遍历
  - 2.2 中序遍历
  - 2.3 后序遍历
  - 2.4 层序遍历
- 3. 常见功能
- - 3.1 二叉树结点个数
  - 3.2 二叉树叶子结点个数
  - 3.3 第K层结点的个数
  - 3.4 二叉树的深度
  - 3.5 判断是不是树是不是完全二叉树
  - 3.6 在二叉树中查找值为x的结点
  - 3.7 拿到每一层的数据
- 4. 二叉树的创建和销毁
- - 4.1 二叉树的创建
  - 4.2 二叉树的销毁

二叉树链式结构实现

前面我们已经对堆进行学习，堆就是一个顺序结构的二叉树，把数组看成二叉树，下面一起学习一下链式结构的二叉树，这里是用递归实现功能

1. 链式二叉树结构

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	BTDataType data;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

2. 二叉树的遍历

首先，我要说明一下递归实现；递归实现一般分为三个步骤（递归三要素）：初步明确函数功能，限制条件，找到实现此功能的等式

单项递归和二叉树递归（多项递归）的区别？

单项递归并没有分支，多项递归是有分支的，这就意味着二叉树更看中整体，单项递归更看重分治。

单项递归和二叉树递归的共同点？

都是分治思想，子问题再分子问题再分子问题的思想

2.1 前序遍历

思想：把树看成整体：根、左子树、右子树，先遍历根再走左子树再走右子树

void BinaryTreePrevOrder(BTNode* root)
{
    //根的情况(到底的限制条件)
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	printf("%c ", root->data);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

2.2 中序遍历

思想：把树看成整体：根、左子树、右子树，先遍历左子树再走根再走右子树

void BinaryTreeInOrder(BTNode* root)
{
    //根的情况(到底的限制条件)
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	BinaryTreeInOrder(root->left);
	printf("%c ", root->data);
	BinaryTreeInOrder(root->right);
}

2.3 后序遍历

void BinaryTreePostOrder(BTNode* root)
{
    //根的情况(到底的限制条件)
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%c ", root->data);
}

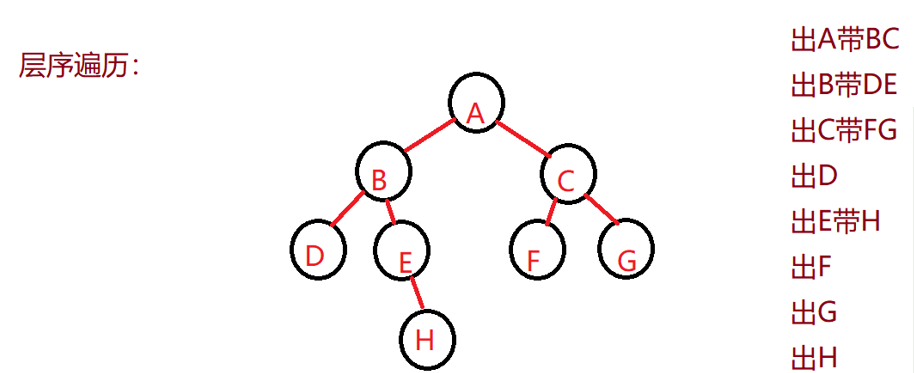
2.4 层序遍历

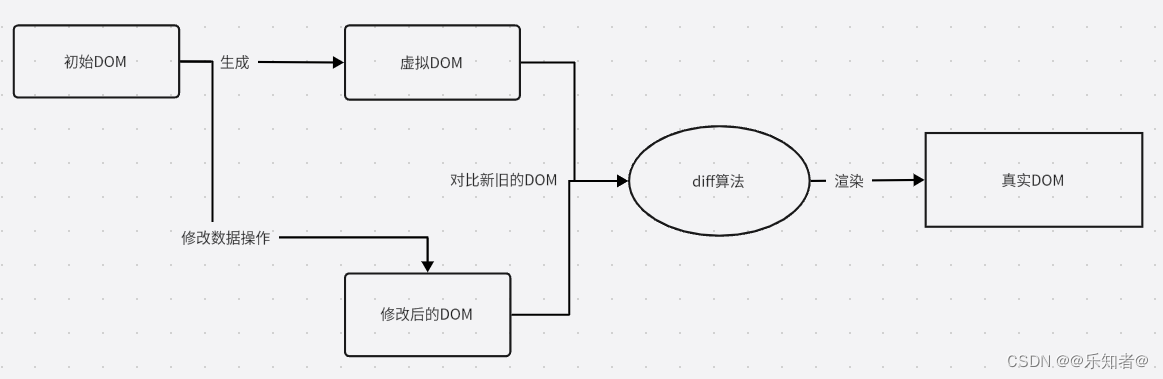
思想：出上一层的同时带着下一层入队列

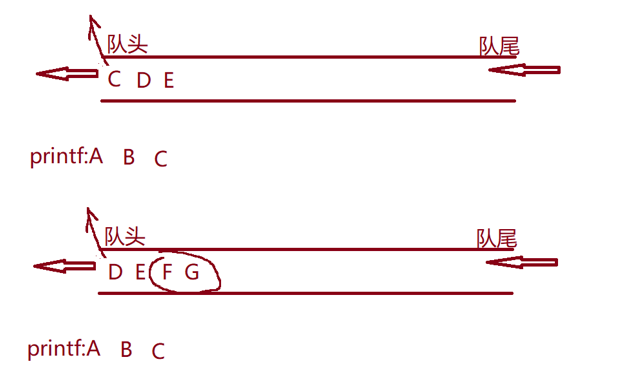
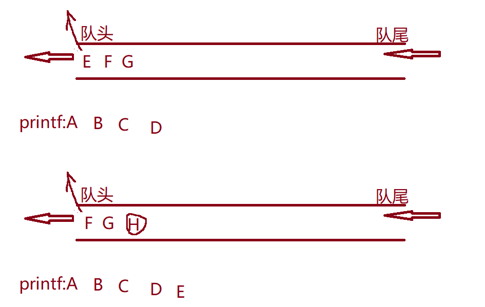
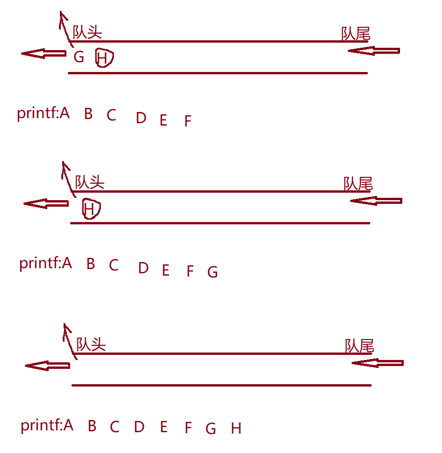
//链式队列的结构
typedef struct BinaryTreeNode* QueueDataType;
typedef struct QueueNode
{
	QueueDataType data;
	struct QueueNode* next;
}QueueNode;
//因为要直接得到队头的元素和队尾的元素
typedef struct QueueLinkList
{
	QueueNode* head; //队头
	QueueNode* tail; //队尾
	int size; //元素总数
}QLL;
//队列初始化
void QLLInit(QLL* queue)
{
	assert(queue);

	queue->head = NULL;
	queue->tail = NULL;
	queue->size = 0;
}
//进队
void QLLPush(QLL* queue, QueueDataType x)
{
	assert(queue);

	QueueNode* newnode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newnode == NULL)
	{
		perror("QLLPush:malloc is failed!\n");
		exit(-1);
	}

	newnode->data = x;
	newnode->next = NULL;

	if (queue->head == NULL)
	{
		queue->head = queue->tail = newnode;
	}
	else
	{
		queue->tail->next = newnode;
		queue->tail = newnode;
	}

	queue->size++;
}
//出队
void QLLPop(QLL* queue)
{
	assert(queue != NULL);
	assert(QLLEmpty(queue) != true);
		
	//只有一个结点时
	if (queue->head->next == NULL)
	{
		free(queue->head); //free的是这个结点的空间，并不是指针
		queue->head = queue->tail = NULL;
	}
	else
	{
		//通常情况
		QueueNode* del = queue->head;
		queue->head = queue->head->next;
		free(del);
		//无需置空
	}

	queue->size--;
}
//拿取队头数据
QueueDataType QLLFront(QLL* queue)
{
	assert(queue != NULL);
	assert(QLLEmpty(queue) != true);

	return queue->head->data;
}
//判空
bool QLLEmpty(QLL* queue)
{
	assert(queue);

	//return queue->size == 0;
	return queue->head == NULL && queue->tail == NULL;
}
//销毁
void QLLDestroy(QLL* queue)
{
	assert(queue);

	QueueNode* cur = queue->head;
	while (cur != NULL)
	{
		QueueNode* del = cur;
		cur = cur->next;
		free(del);
		del = NULL;
	}

	queue->head = queue->tail = NULL;
	queue->size = 0;
}

//层序遍历实现
void BinaryTreeLevelOrder(BTNode* root)
{
	QLL queue;
	QLLInit(&queue);
    //根先入队列
	if (root != NULL) {
		QLLPush(&queue, root);
	}
	//队列不为NULL的时候进行出队头带下层数据入队操作
	while (QLLEmpty(&queue) != true)
	{
        //出队头操作
		BTNode* front = QLLFront(&queue);
		printf("%c ", front->data);
		QLLPop(&queue);
        //带下一层进队
		if (front->left != NULL)
		{
			QLLPush(&queue, front->left);
		}
		if (front->right != NULL)
		{
			QLLPush(&queue, front->right);
		}
	}
	printf("\n");
	QLLDestroy(&queue);
}

说明：为什么递归不画图来解决呢？

多项递归画图是很难理解的，因为他不是我们逻辑上想的，就拿前序遍历来说，首先是根，再遍历左子树再遍历右子树这样循环来走，但是在实际递归中逻辑是左子树走到底，直到NULL时返回访问右子树，如果说是画图是理解不了二叉树递归的，这里我们就要扣住树的结构：根、左子树、右子树，这样是我们逻辑上的实现，并不是实际中的过程实现，这里我需要说明一下，画图是为了在原有基础上来进行纠错，这里纠正的错也是和根的限制条件有关，这里我还会出几期二叉树的相关练习，到时候希望大佬们看看就能理解了二叉树递归！

3. 常见功能

3.1 二叉树结点个数

递归三要素解决问题

首先二叉树想到整体结构：根、左子树、右子树

函数功能：求二叉树结点的个数

限制条件：根为NULL的时候就不是一个结点（起初的结束条件：针对根来说）

等式：计算左子树中的结点个数和右子树的结点个数，最后加上根这个结点

int BinaryTreeSize(BTNode* root)
{
	if (root == NULL) {
		return 0;
	}

	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

代码分析

上述列出来的思路就是实现思路，这里注意的是树的整体结构，我一直扣的就是整体结构，等式中写的也是整体结构的逻辑；这里来看代码很简单就是根和左子树和右子树结构

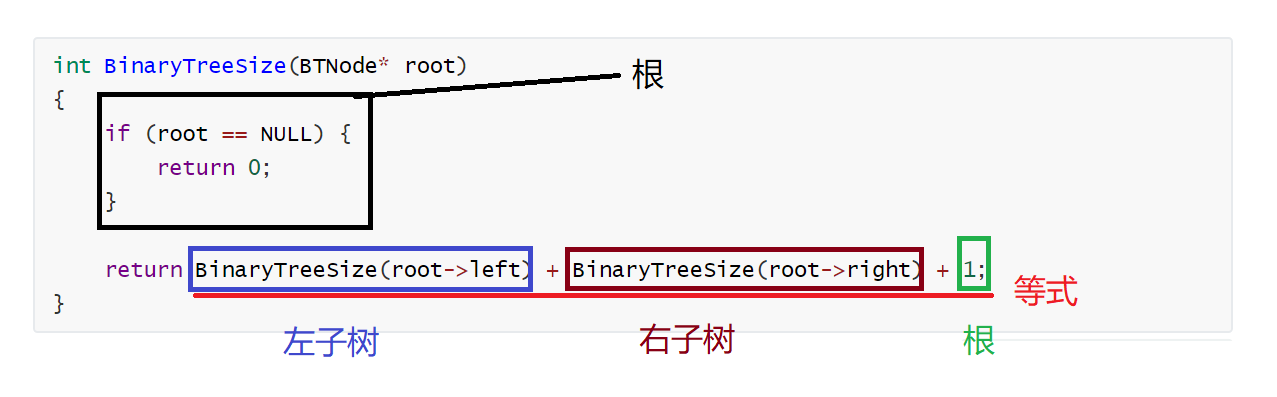
为什么不写子结构：根、左孩子、右孩子？

原因就是如果写成子结构的话就不是整体，而是把整体分为多个相同的结构来讨论，这里就不是整体观念就很容易陷进去，为什么二叉树递归难，难就难在你没扣住整体，而是扣住的是子结构，如果扣住子结构那就很容易陷进去，只要陷进去了就不是我们自己想的逻辑，而是实际递归的过程逻辑，实际递归的过程逻辑和我们想的逻辑有很大的区别

为什么首先要有个前提：树的结构：根、左子树、右子树？

原因很简单，我们考虑整体就少不了这个结构，这是我们首先要考虑的问题；另外也是因为这里三要素中的实现是离不开这个整体结构的，如果离开了整体结构就又被陷进去了

限制条件是怎么来限制的？

首先我们考虑的结构就是树的整体结构：根、左子树、右子树，我们不可能是来对左右子树来限制吧，因为左右子树中有很多结点，从整体上来说是考虑不到的，另外你只要考虑左右子树中的结点恭喜你，你又被陷进去出不来了哈哈，所以这里的限制条件是针对根来讲的：也就是根的起初的结束条件以及和题意的联系

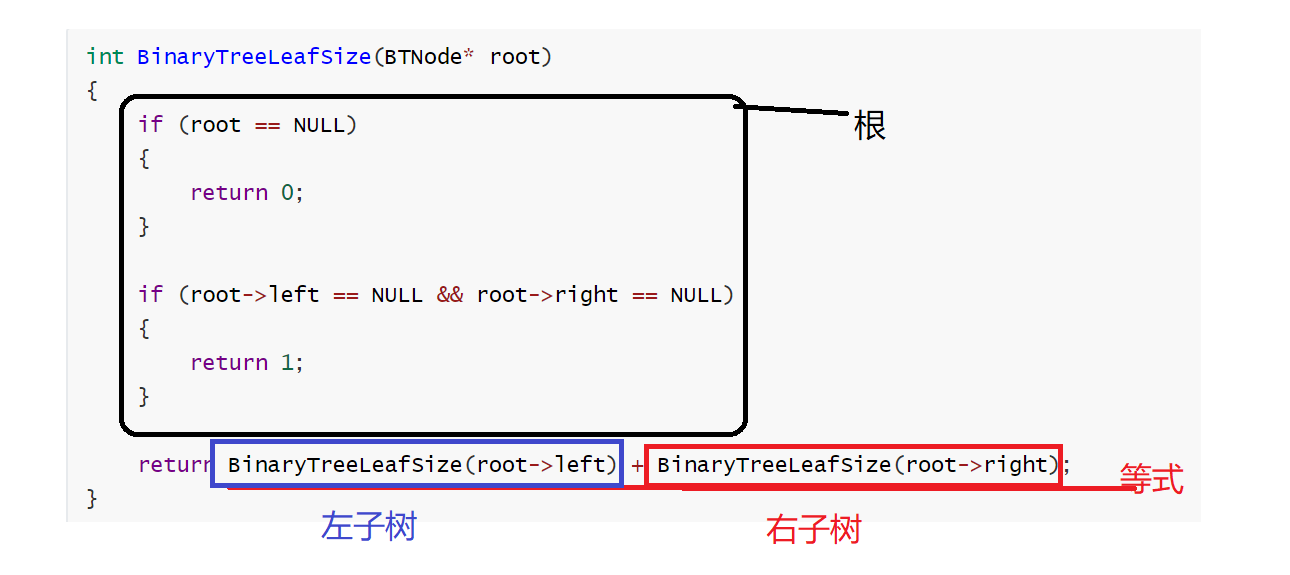
3.2 二叉树叶子结点个数

递归三要素解决问题

前提：树的结构：根、左子树、右子树

函数功能：求二叉树叶子节点的个数

限制条件：root=NULL的时候就不是叶子结点，根的左右孩子是空的时候但根不是空的时候就是叶子结点

等式：在左右子树中找叶子节点，左右子树中的叶子结点之和也就是树的叶子结点

int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

代码分析

3.3 第K层结点的个数

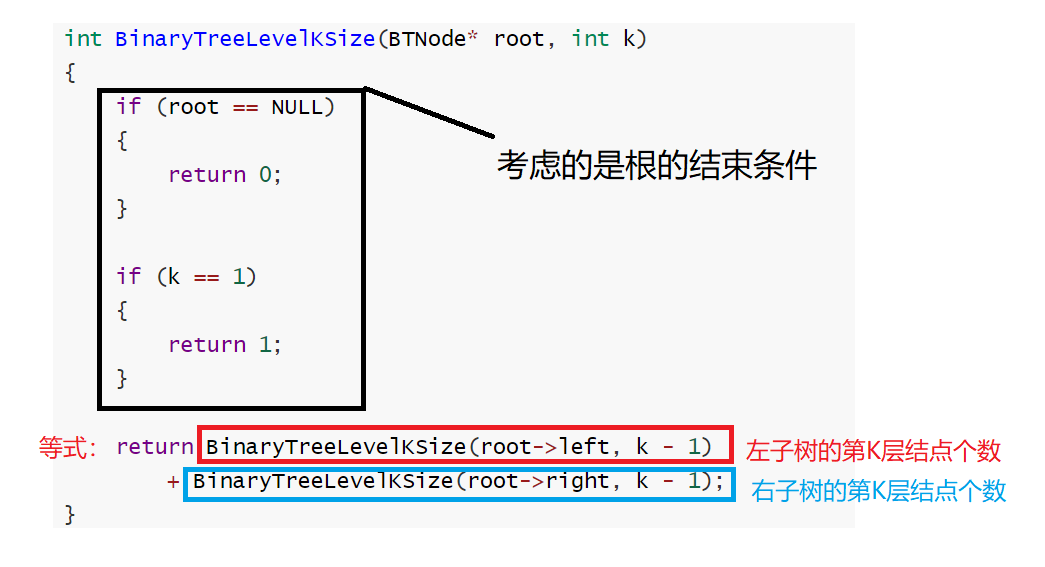
递归三要素解决问题

前提：树的结构：根、左子树、右子树

函数功能：求第K层结点的个数

限制条件：root=NULL(起初的结束条件)，根所处的是第一层所以K=1的时候返回1（题意结束条件）

等式：在左右子树的第k-1层中的结点个数（因为第一层是根，所以第K-1层才是我们要求的第K层）

int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	return BinaryTreeLevelKSize(root->left, k - 1)
		+ BinaryTreeLevelKSize(root->right, k - 1);
}

代码分析

3.4 二叉树的深度

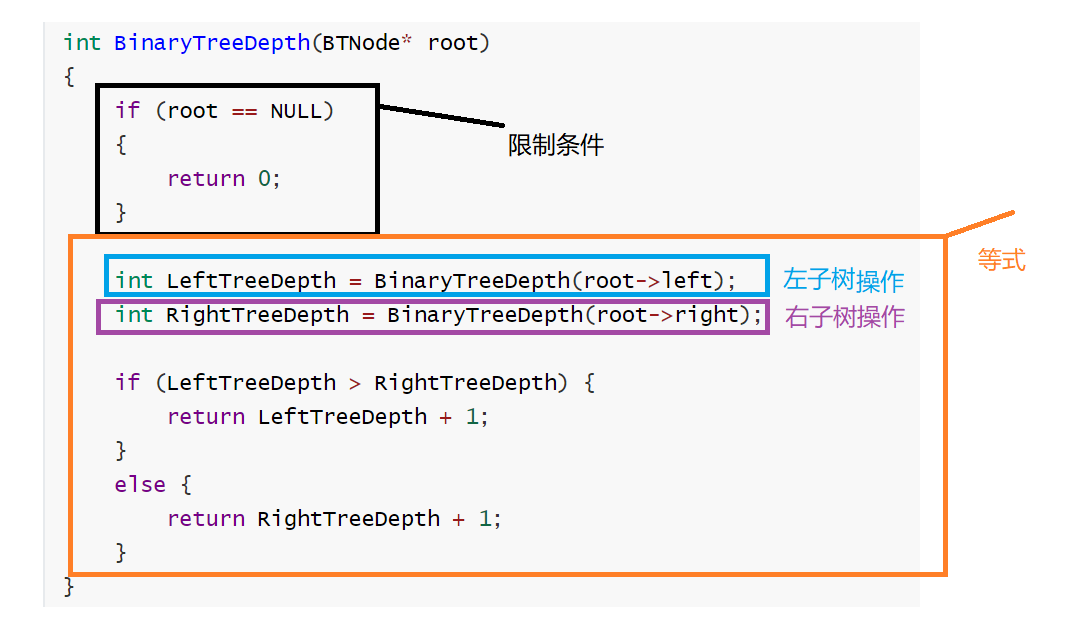
递归三要素解决问题

前提：树的结构：根、左子树、右子树

函数功能：求树的深度

限制条件：根为NULL时结束

等式：树的根是第一层，那么我们只用计算出左子树和右子树的哪个深度大就再加上1（根的深度）就是树的深度

int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	int LeftTreeDepth = BinaryTreeDepth(root->left);
	int RightTreeDepth = BinaryTreeDepth(root->right);

	if (LeftTreeDepth > RightTreeDepth) {
		return LeftTreeDepth + 1;
	}
	else {
		return RightTreeDepth + 1;
	}
}

代码分析

没进行优化的代码：

int BinaryTreeDepth(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	if (BinaryTreeDepth(root->left) > BinaryTreeDepth(root->right)) {
		return BinaryTreeDepth(root->left) + 1;
	}
	else {
		return BinaryTreeDepth(root->right) + 1;
	}
}

这个代码也是对的，但是时间复杂就要多了1倍，因为判断中用到递归了，找到了并没有记录深度，也就进入判断中的递归，再此递归一次，这样时间复杂度就增了1倍。

3.5 判断是不是树是不是完全二叉树

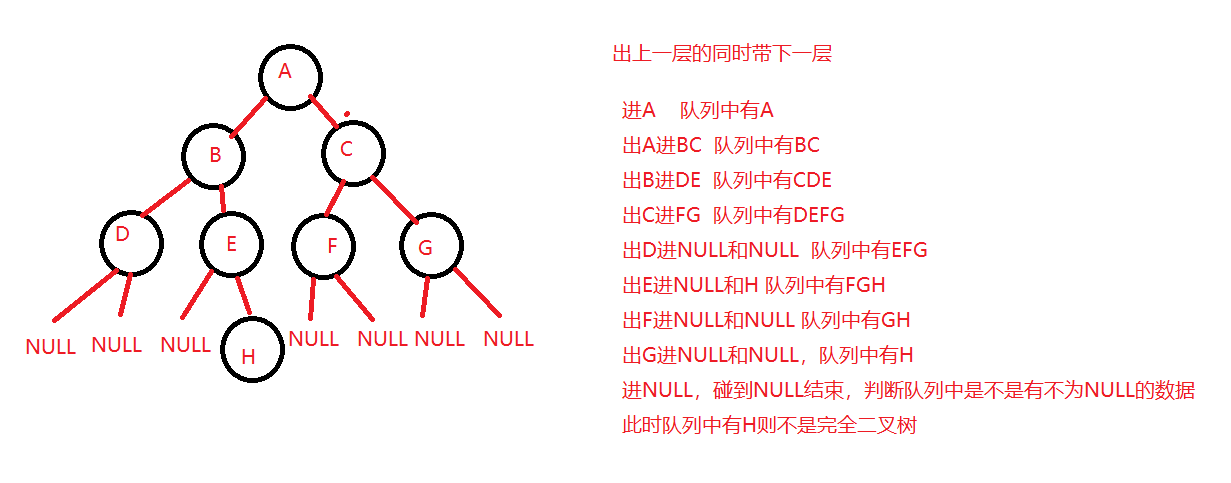
思路：

完全二叉树的性质：前K-1层是满二叉树，最后一层是从左到右是连续的

思路：用层序遍历来解决，出上一层的同时带下一层的数据，知道遇到NULL的时候就要进行判断队列中是不是还有不为NULL的值，如果有就不是完全二叉树，没有则是

bool BinaryTreeComplete(BTNode* root)
{
	QLL queue;
	QLLInit(&queue);
	if (root != NULL)
	{
		QLLPush(&queue, root);
	}

	//拿到每层的
	while (QLLEmpty(&queue) != true)
	{
		BTNode* front = QLLFront(&queue);
		QLLPop(&queue);

		//当这层遇到NULL的时候进行判断
		if (front == NULL)
		{
			break;
		}
		else
		{
			QLLPush(&queue, front->left);
			QLLPush(&queue, front->right);
		}
	}
    
	//出到NULL进行检查
	//如果后面有非NULL就不是完全二叉树
	while (QLLEmpty(&queue) != true)
	{
		BTNode* front = QLLFront(&queue);
		QLLPop(&queue);
		//不为NULL说明最后一层不是连续的
		if (front != NULL)
		{
			QLLDestroy(&queue);
			return false;
		}
	}
	
	QLLDestroy(&queue);
	return true;
}

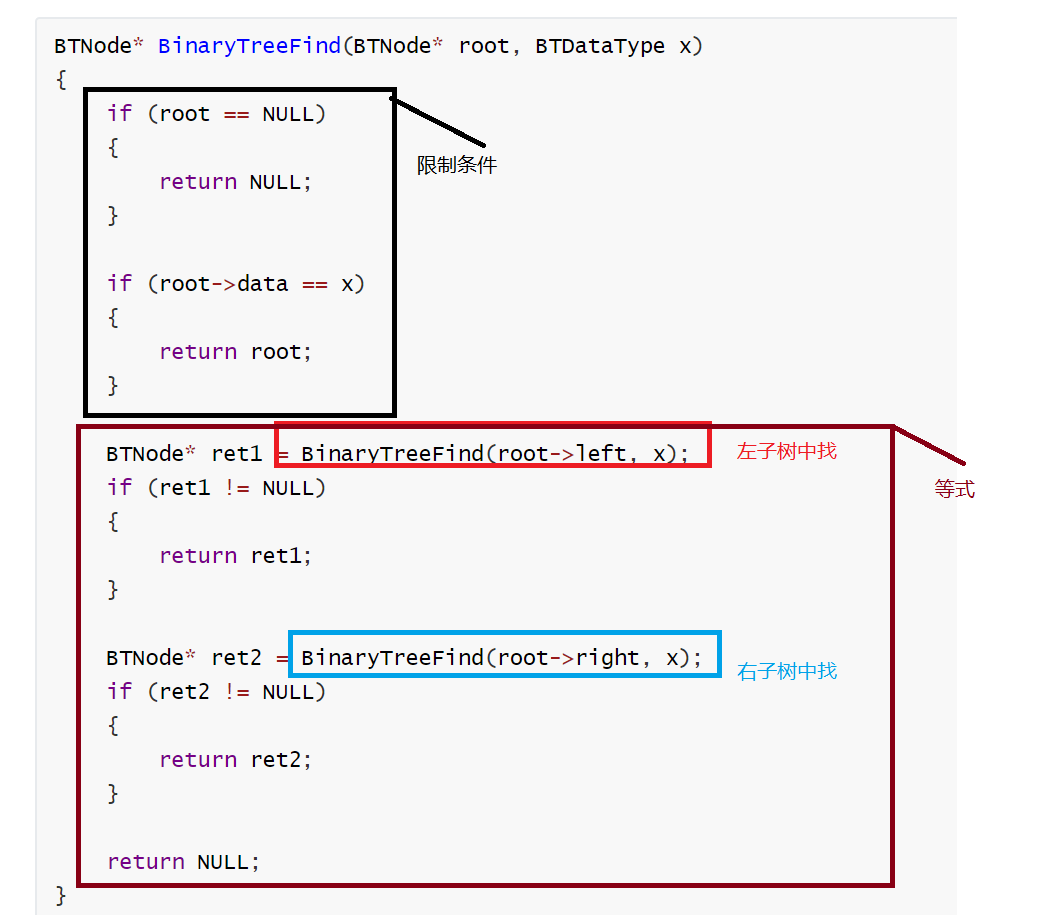
3.6 在二叉树中查找值为x的结点

递归三要素解决问题

前提：树的结构：根、左子树、右子树

函数功能：在二叉树中查找值为x的结点

限制条件：root=NULL时结束，root->val=x时找到了就结束

等式：在根里面找，在左子树和右子树里面找

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->data == x)
	{
		return root;
	}

	BTNode* ret1 = BinaryTreeFind(root->left, x);
	if (ret1 != NULL)
	{
		return ret1;
	}

	BTNode* ret2 = BinaryTreeFind(root->right, x);
	if (ret2 != NULL)
	{
		return ret2;
	}

	return NULL;
}

代码分析

错误列举


BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->data == x)
	{
		return root;
    }

	return BinaryTreeFind(root->left, x) || BinaryTreeFind(root->right, x);
}

为什么逻辑上是对的，但是是错的？

最后的return的意思翻译过来就是在左子树里面找，找到了就返回，不进右子树，如果左子树中没找到就进右子树，找到了返回，如果都没找到就直接返回NULL；逻辑上是对的，但是呢，这里我们返回的是指针，指针的的关系不能用逻辑关系来表达，所以是错的

3.7 拿到每一层的数据

思路

也是围绕层序遍历来写：记录每一层的结点树来出队列就行了，这里也是层序遍历的知识是主要的，就不再进行讨论了


void EveryLayer(BTNode* root)
{
	QLL queue;
	int levelCount = 0;
	QLLInit(&queue);
	if (root != NULL) {
		QLLPush(&queue, root);
		//第一层就是一个数据
		levelCount = 1;
	}

	while (QLLEmpty(&queue) != true)
	{
		while (levelCount--)
		{
			BTNode* front = QLLFront(&queue);
			printf("%c ", front->data);
			QLLPop(&queue);
			if (front->left != NULL)
			{
				QLLPush(&queue, front->left);
			}
			if (front->right != NULL)
			{
				QLLPush(&queue, front->right);
			}
		}
		//下一层的个数
		levelCount = QLLSize(&queue);
		printf("\n");
	}
	
	QLLDestroy(&queue);
}

结合上述题就很容易看出实际上我们写代码来划分的话也是树的整体结构：根、左子树、右子树，时刻把握着树的整体结构，这个结构充分体现在等式中，同时也影响到了限制条件，限制条件中只用管根的结束条件以及形成条件，其他的不用管，这就是在代码中实现的过程，这里我就不在画图，觉得这个过程不能实现我说的对应的功能的时候你就画图去尝试理解一下，谢谢

4. 二叉树的创建和销毁

4.1 二叉树的创建

思路：

这里用到前序遍历来创建，也就是数组的元素按个放进根的数据域中

限制条件：就是当元素为#，代表的是二叉树中的NULL

BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	//形成条件
	if (a[(*pi)] == '#')
	{
		(*pi)++;
		return NULL;
	}

	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	if (root == NULL)
	{
		perror("BinaryTreeCreate: malloc is failed!\n");
		exit(-1);
	}
	//根
	root->data = a[(*pi)++];

	//左右子树
	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a, pi);

	return root;
}
void Test2()
{
	char str[] = { 'A','B','D','#','#','E','#','H','#','#','C','F','#','#','G','#','#' };

	int i = 0;
	BTNode* root = BinaryTreeCreate(str, &i);
}

4.2 二叉树的销毁

//二级指针
void BinaryTreeDestory(BTNode** root)
{
	if ((*root) == NULL)
	{
		return;
	}
	BinaryTreeDestory(&((*root)->left));
	BinaryTreeDestory(&((*root)->right));
	free((*root));
	*root = NULL;
}

void FirstPointBinaryTreeDestory(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	FirstPointBinaryTreeDestory(root->left);
	FirstPointBinaryTreeDestory(root->right);
	free(root);
	//root = NULL;(没必要）
}//需要说明的是用这个函数调用后要对root置空