LeetCode热题HOT100
139. 单词拆分
题目:给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
思路分析: 使用一个布尔数组 dp[],大小为 s.length() + 1,其中 dp[i] 表示我们是否可以使用字典中的单词从索引0到索引i-1拆分字符串s。基本情况是 dp[0] = true,因为空字符串总是可以被拆分。然后,我们从左到右遍历字符串 s,对于每个索引 i,我们遍历所有可能的分割点 j,使得 0 <= j < i。如果 dp[j] 为 true,这意味着我们可以从0到j-1拆分字符串,且从j到i-1的子字符串在字典中,则我们可以从0到i-1拆分字符串。我们将 dp[i] 设置为true,并退出内部循环。最后,我们返回 dp[s.length()],它表示我们是否可以使用字典中的单词拆分整个字符串。
class Solution {
// 定义一个方法,用于判断给定的字符串 s 是否可以被拆分成字典中的单词
public boolean wordBreak(String s, List<String> wordDict) {
// 定义一个布尔类型的数组 dp,长度为 s.length() + 1
boolean[] dp = new boolean[s.length() + 1];
// 将 dp[0] 设为 true,因为空字符串总是可以被拆分
dp[0] = true;
// 从 1 到 s.length() 遍历每个字符串
for (int i = 1; i <= s.length(); i++) {
// 从 0 到 i 遍历每个可能的拆分点
for (int j = 0; j < i; j++) {
// 如果 dp[j] 为 true,意味着 s 的前半部分可以被拆分成字典中的单词,且 s 的后半部分也在字典中,则将 dp[i] 设为 true
if (dp[j] && wordDict.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
// 返回 dp[s.length()],表示 s 是否可以被拆分成字典中的单词
return dp[s.length()];
}
}
142. 环形链表 II
题目:给定一个链表的头节点 head ,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
如果链表中有某个节点,可以通过连续跟踪 next 指针再次到达,则链表中存在环。 为了表示给定
链表中的环,评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。
如果 pos 是 -1,则在该链表中没有环。注意:pos 不作为参数进行传递,仅仅是为了标识链表的实际情况。
不允许修改 链表
**示例 1:
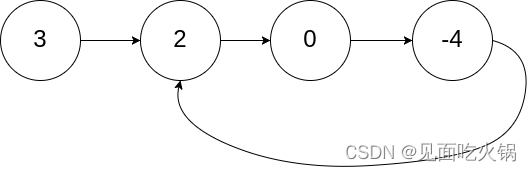
输入:head = [3,2,0,-4], pos = 1
输出:返回索引为 1 的链表节点
解释:链表中有一个环,其尾部连接到第二个节点。
思路分析: 使用快慢指针,快指针每次走两步,慢指针每次走一步,如果链表存在环,那么快慢指针一定会相遇。在相遇时,我们可以通过计算快指针和慢指针走过的节点数来确定环中节点的个数。然后,将快指针重新指向头节点,让其先走 n 步,再让快慢指针同时走,相遇的节点即为环的入口节点。
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null) { // 如果链表为空,则直接返回 null
return null;
}
ListNode fast = head; // 定义快指针,指向链表头
ListNode slow = head; // 定义慢指针,指向链表头
boolean flag = false; // 定义标志位,判断链表是否存在环
// 使用快慢指针判断链表是否存在环
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (fast == slow) { // 如果快慢指针相遇,则说明链表存在环
flag = true; // 将标志位设为 true
break;
}
}
if (!flag) { // 如果标志位为 false,则说明链表不存在环,直接返回 null
return null;
} else { // 如果标志位为 true,则说明链表存在环
int n = 1; // 定义计数器,记录环中节点的个数
fast = fast.next;
while (fast != slow) { // 统计环中节点的个数
n++;
fast = fast.next;
}
fast = head; // 将快指针重新指向头节点
slow = head; // 将慢指针重新指向头节点
for (int i = 0; i < n; i++) { // 让快指针先走 n 步
fast = fast.next;
}
// 快慢指针同时走,相遇的节点即为环的入口节点
while (fast != slow) {
fast = fast.next;
slow = slow.next;
}
return fast; // 返回环的入口节点
}
}
}
146. LRU 缓存
题目:请你设计并实现一个满足 LRU (最近最少使用) 缓存 约束的数据结构。
实现 LRUCache 类:
LRUCache(int capacity) 以 正整数 作为容量 capacity 初始化 LRU 缓存
int get(int key) 如果关键字 key 存在于缓存中,则返回关键字的值,否则返回 -1 。
void put(int key, int value) 如果关键字 key 已经存在,则变更其数据值 value ;
如果不存在,则向缓存中插入该组 key-value 。如果插入操作导致关键字数量超过 capacity ,
则应该 逐出 最久未使用的关键字。
函数 get 和 put 必须以 O(1) 的平均时间复杂度运行。
**示例 1:
输入
[“LRUCache”, “put”, “put”, “get”, “put”, “get”, “put”, “get”, “get”, “get”]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]
解释
LRUCache lRUCache = new LRUCache(2);
lRUCache.put(1, 1); // 缓存是 {1=1}
lRUCache.put(2, 2); // 缓存是 {1=1, 2=2}
lRUCache.get(1); // 返回 1
lRUCache.put(3, 3); // 该操作会使得关键字 2 作废,缓存是 {1=1, 3=3}
lRUCache.get(2); // 返回 -1 (未找到)
lRUCache.put(4, 4); // 该操作会使得关键字 1 作废,缓存是 {4=4, 3=3}
lRUCache.get(1); // 返回 -1 (未找到)
lRUCache.get(3); // 返回 3
lRUCache.get(4); // 返回 4
思路分析: 使用双向链表和哈希表来实现LRU缓存。在双向链表中,每个节点保存了该节点的键值对,并且维护了前驱和后继指针。在哈希表中,每个键都映射到对应的节点。当访问一个键时,如果哈希表中包含该键,则将该节点移动到链表头部,并返回节点的值;如果哈希表中不包含该键,则返回-1。在插入一个键值对时,如果哈希表中不包含该键,则创建一个新节点并将其添加到链表头部和哈希表中;如果哈希表中包含该键,则删除旧节点,创建一个新节点并将其添加到链表头部和哈希表中。当缓存达到容量限制时,删除链表最后一个节点和哈希表中对应的项。
class LRUCache {
// 双向链表和哈希表
DoubleLinkedList doubleLinkedList;
HashMap<Integer, Node> map;
// 缓存最大容量
int capacity;
public LRUCache(int capacity) {
// 初始化双向链表和哈希表
doubleLinkedList = new DoubleLinkedList();
map = new HashMap<>();
// 初始化缓存最大容量
this.capacity = capacity;
}
public int get(int key) {
// 如果哈希表中不包含该键,则返回-1
if (!map.containsKey(key)) {
return -1;
} else {
// 如果哈希表中包含该键,则将该节点移动到链表头部,并返回节点的值
Node cur = map.get(key);
doubleLinkedList.delete(cur);
doubleLinkedList.addFirst(cur);
return cur.val;
}
}
public void put(int key, int value) {
// 创建新节点
Node newNode = new Node(key, value);
if (!map.containsKey(key)) {
// 如果哈希表中不包含该键,则将新节点添加到链表头部和哈希表中
if (map.size() == capacity) {
// 如果缓存已满,则删除链表最后一个节点和哈希表中对应的项
int k = doubleLinkedList.deleteLast();
map.remove(k);
}
doubleLinkedList.addFirst(newNode);
map.put(key, newNode);
} else {
// 如果哈希表中包含该键,则删除旧节点,将新节点添加到链表头部和哈希表中
doubleLinkedList.delete(map.get(key));
doubleLinkedList.addFirst(newNode);
map.put(key, newNode);
}
}
}
class Node {
// 节点键和值
int key;
int val;
// 节点的前驱和后继
Node pre;
Node next;
public Node(int key, int val) {
// 初始化节点
this.key = key;
this.val = val;
}
}
class DoubleLinkedList {
// 双向链表的头节点和尾节点
Node head;
Node tail;
public DoubleLinkedList() {
// 初始化双向链表
head = new Node(-1, -1);
tail = new Node(-1, -1);
head.next = tail;
tail.pre = head;
}
public void addFirst(Node node) {
// 将节点添加到链表头部
node.next = head.next;
node.pre = head;
head.next.pre = node;
head.next = node;
}
public int delete(Node node) {
// 删除指定节点
node.pre.next = node.next;
node.next.pre = node.pre;
return node.key;
}
public int deleteLast() {
// 删除链表最后一个节点
return delete(tail.pre);
}
}
![[前端基础]Node.js简单操作,手把手教你搭建一个轻量级应答服务器(会继续补充操作细节,欢迎讨论)](https://img-blog.csdnimg.cn/82c4d5d9e7744231bb19d57e2bd0e89e.png)