[LeetCode复盘] LCCUP'23春季赛 20230422
- 一、总结
- 二、 1. 补给马车
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 三、2. 探险营地
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 四、 3. 最强祝福力场
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 五、 4. 传送卷轴
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 六、 5. 魔法棋盘(以后补)
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- 七、参考链接
一、总结
- 半年前秋季赛3题,这次春季赛4题,有进步!
- T1 模拟。
- T2 模拟。
- T3 暴力枚举/扫描线。
- T4 最短路+二分。
- T5 状压DP。

二、 1. 补给马车
链接: 1. 补给马车
1. 题目描述

2. 思路分析
按题意模拟即可。
- py的话,可以直接切片赋值,非常方便。
- 复杂度n方。
3. 代码实现
class Solution:
def supplyWagon(self, a: List[int]) -> List[int]:
n = len(a)
if n <= 3:
return [sum(a)]
d = n - n // 2
for _ in range(d):
i = 0
mx = a[0]+a[1]
for j in range(1,len(a)-1):
s = a[j]+a[j+1]
if s < mx:
mx = s
i = j
a[i:i+2] = [mx]
return a
三、2. 探险营地
链接: 2. 探险营地
1. 题目描述

2. 思路分析
贴模板。
- 都乘到一起找质因数就是分别找质因数然后去重,因此用set记录并集即可。
3. 代码实现
class Solution:
def adventureCamp(self, a: List[str]) -> int:
s = set(x for x in a[0].split('->') if x)
# print(s)
ans = -1
mx = 0
for i in range(1,len(a)):
p = set(x for x in a[i].split('->') if x)
x = len(s)
s |= p
add = len(s) - x
if add > mx:
mx = add
ans = i
return ans
四、 3. 最强祝福力场
链接: 3. 最强祝福力场
1. 题目描述

2. 思路分析
- 扫描线不会,但这题n=100,因此可以暴力。
- 由于最优矩形一定是切出来的,因此左边一定是某个矩形的左边,下边一定是某个矩形的下边。
- 那么最优矩形的左下角是可以枚举的。具体见代码。
- 枚举每个左下角,计算它在几个矩形里即可。
- 每个数据都乘2,避免浮点运算。
3. 代码实现
class Solution:
def fieldOfGreatestBlessing(self, a: List[List[int]]) -> int:
for i,(x,y,d) in enumerate(a):
a[i] = (x*2,y*2,d*2)
xx = []
yy = []
for x,y,d in a:
xx.append(x-d//2)
yy.append(y-d//2)
ans = 1
for x1 in xx:
for y1 in yy:
cnt = 0
for x,y,d in a:
if x-d//2<=x1<=x+d//2 and y-d//2<=y1<=y+d//2:
cnt += 1
ans = max(ans,cnt)
return ans
五、 4. 传送卷轴
链接: 4. 传送卷轴
1. 题目描述

2. 思路分析
- 题目只问传送后到T的步数,因此可以直接先从T出发计算最短路,如果到不了S直接返回-1。
- 这个最短路作为玩家被传送后,带着debuff到T的步数。
- 魔王可以在s-t的任意格子上使玩家传送到镜像,注意,必须是玩家在’.‘(不包括S),镜像的位置必须是’.'/‘S’。
- 那么可以预处理每个位置的权值p,玩家经过这个位置的话,魔王的操作可以让玩家步骤变成max{镜像位置的dis},若这个位置不能进行传送,则p=0,因为只计算传送后的距离。
- 预处里完P后,玩家需要找一条s->t的连通路径,魔王可以选这个路径上的最大位置。那么玩家的目的就是最小化路径上的最大值。警觉,可以二分。
- 设这个最大值是x,那么路径上的所有值需要<=x,显然x越大越能满足;x越小越不可以满足。
- 或者可以dij,直接用堆,玩家每次都选最小的相邻位置并更新mx,走到T即可。代码会短一些
3. 代码实现
DIRS = [(0,1),(0,-1),(1,0),(-1,0)]
class Solution:
def challengeOfTheKeeper(self, g: List[str]) -> int:
m,n = len(g),len(g[0])
dis = [[inf]*n for _ in range(m)]
def inside(x,y):
return 0<=x<m and 0<=y<n
def find_t():
for i in range(m):
for j in range(n):
if g[i][j] == 'T':
return i,j
def find_s():
for i in range(m):
for j in range(n):
if g[i][j] == 'S':
return i,j
tx,ty = find_t()
sx,sy = find_s()
dis[tx][ty] = 0
q = deque([(tx,ty)])
while q:
x,y = q.popleft()
d = dis[x][y] + 1
for dx,dy in DIRS:
a,b = x+dx,y+dy
if inside(a,b) and dis[a][b] > d and g[a][b] != '#':
dis[a][b] = d
q.append((a,b))
if dis[sx][sy] == inf:
return -1
def get(x,y):
if g[x][y] != '.':
return 0
r = 0
if g[x][n-y-1] != '#':
r = max(r,dis[x][n-y-1])
if g[m-x-1][y] != '#':
r = max(r,dis[m-x-1][y])
return r
ans = 0
top = 0
p = [[inf]*n for _ in range(m)]
for i in range(m):
for j in range(n):
if dis[i][j] < inf:
p[i][j] = get(i,j)
if p[i][j] < inf:
top = max(top,p[i][j])
q = [(0,sx,sy)]
vis = [[False]*n for _ in range(m)]
vis[sx][sy] = True
while q:
d,x,y = heappop(q)
ans = max(ans,d)
for dx,dy in DIRS:
a,b = x + dx, y + dy
if a==tx and b ==ty:
return ans
if not inside(a,b) or g[a][b] == '#' or vis[a][b] or p[a][b] == inf:continue
vis[a][b] = True
heappush(q,(p[a][b],a,b))
return -1
# # 二分做法
# vis = [[-10]*n for _ in range(m)]
# # 是否存在路径,路径上的权值都<=x
# def ok(z):
# vis[sx][sy] = z
# def dfs(x,y):
# if x==tx and y == ty:
# return True
# for dx,dy in DIRS:
# a,b = x+dx,y+dy
# if not inside(a,b) or g[a][b] == '#':
# continue
# if p[a][b] > z:
# continue
# if a==tx and b == ty:
# return True
# if vis[a][b] != z:
# vis[a][b] = z
# if dfs(a,b):
# return True
# # print(x,y)
# return False
# return dfs(sx,sy)
# # print(p)
# # print(ok(7))
# ans = bisect_left(range(top+1),True,key=ok)
# # print(top,ans)
# if ans == top+1:
# return -1
# return ans
六、 5. 魔法棋盘(以后补)
链接: 5. 魔法棋盘
1. 题目描述
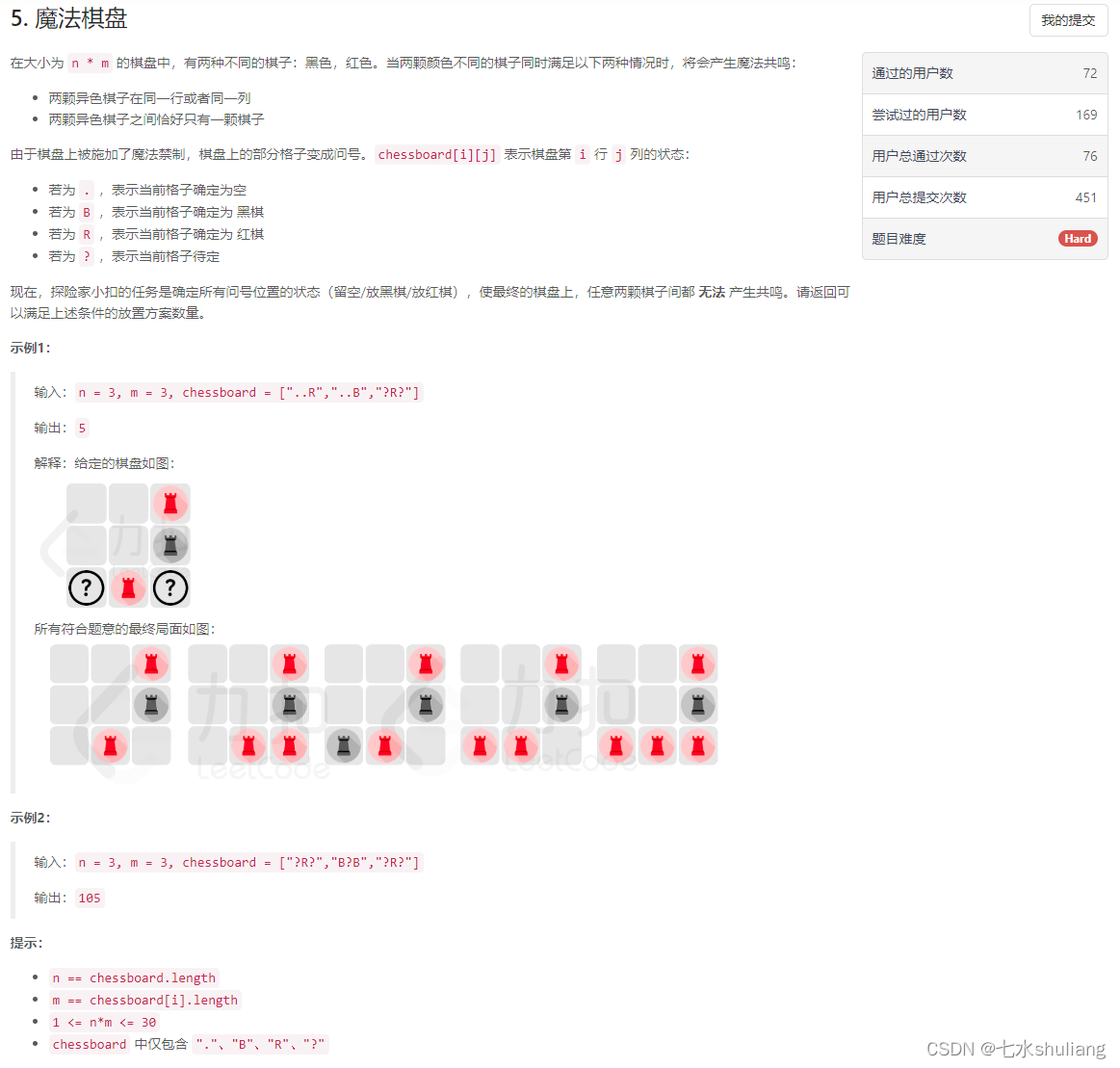
2. 思路分析
- 直接暴力状压,但是TLE了。想想也是,全问号的情况下,每个位置枚举空和R就2^30次方了。
- 等听完课再补。
3. 代码实现
class Solution:
def getSchemeCount(self, n: int, m: int, g: List[str]) -> int:
stat = []
for i in range(n):
for j in range(m):
stat.append(g[i][j])
@cache
def dfs(i,stat):
if i == n*m:
return 1
if stat[i] != '?':
return dfs(i+1,stat)
def check(a): # check一个一个方向上的一条是否合法
z = []
for c in a:
if c in 'RB?':
z.append(c)
if len(z) <= 2:
return True
# if len(set(z)) == 1:
# return True
for i in range(2,len(z)):
x,y = z[i],z[i-2]
if x != y and x != '?' and y !='?' and z[i-1] !='?':
return False
return True
def ok(x,y): # check这个点所在的行列是否合法
a =[]
for i in range(n):
if p[i][y] in 'RB?':
a.append(p[i][y])
if len(a)>=3 and a[-1]!='?' and a[-2]!='?' and a[-3]!='?' and a[-1]!=a[-3]:
return False
a = []
for j in range(m):
if p[x][j] in 'RB?':
a.append(p[x][j])
if len(a)>=3 and a[-1]!='?' and a[-2]!='?' and a[-3]!='?' and a[-1]!=a[-3]:
return False
return True
p = [['']*m for _ in range(n)] # 还原出棋盘
s = list(stat)
for x in range(n):
for y in range(m):
p[x][y] = s[x*m + y]
ans = 0
x,y = divmod(i,m)
for c in 'RB.':
p[x][y] = c
if ok(x,y) :
s[i] = c
ans += dfs(i+1,tuple(s))
return ans
return dfs(0,tuple(stat))


![[前端基础]异步操作(还没写完)](https://img-blog.csdnimg.cn/bb3f9d38abdd42898c30fbade8637050.png)