一、前言

我们前面讲到的Blinn-Phong着色，Whitted-Style光线追踪都有一定问题，那就是它们并没有严格的按照物理规则定义各个变量。比如，Blinn-Phong中的光的强度，并没有一个确切的单位。同时Whitted-Style光线追踪我们也做了很多简化处理，例如能量的吸收衰减，我们只是凭借感觉直接的给了一个百分比，并没有严格按照物理规则计算和定义。而辐射度量学(radiometry)的方法能能更精确的给出我们这些信息(包括光线的定义以及表面材质与光线的作用)，从而达到更为真实的效果。

辐射度量学定义了一系列的概念，包括光线在空间中的属性等，用它们来精确的表述在真实的物理环境下光线的作用和传播，当然辐射度量学仍然是依据几何光学来做的，也就是在这里我们仍然认为光是沿直线传播的，没有波动性。

二、Radiant Energy and Flux (Power)—辐射能和通量(功率)

Radiant Energy，辐射能，也就是能量，记作Q，单位J，焦耳，这个大家很好理解，高中物理中经常提到。那么Radiant Flux是什么呢，它表示辐射通量，大家其实也很熟，只不过这里换了个名字，它用Φ表示，计算公式Φ=dQ/dt，单位W，瓦特，但这里表示的不是光的功率，虽然计算上面来讲是一样的，在光学中功率的单位用lm来表示，也就是lumen(流明)。而辐射通量我们可以简单的把它理解为光的“亮度”。

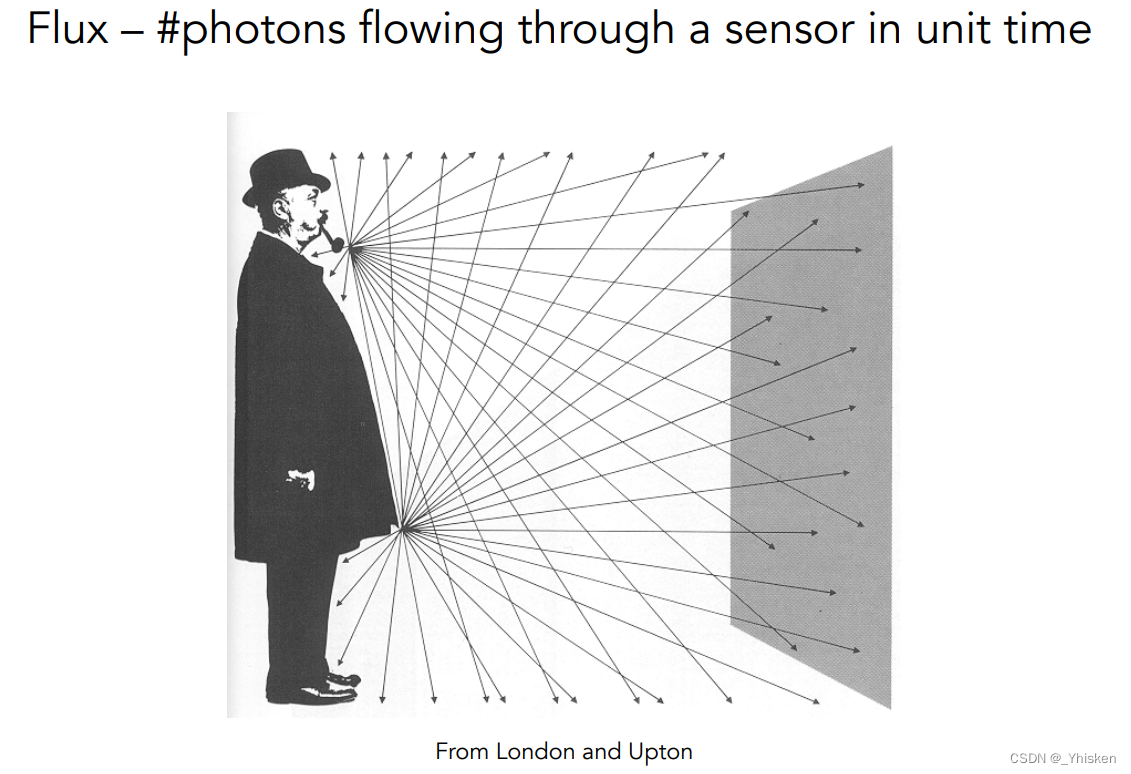
而辐射通量究竟是什么呢？我们知道光源会发出很多光子，假设有一个平面，然后光线会打到这个平面，那么单位时间内通过这个平面的光子的数量就是它的辐射通量。

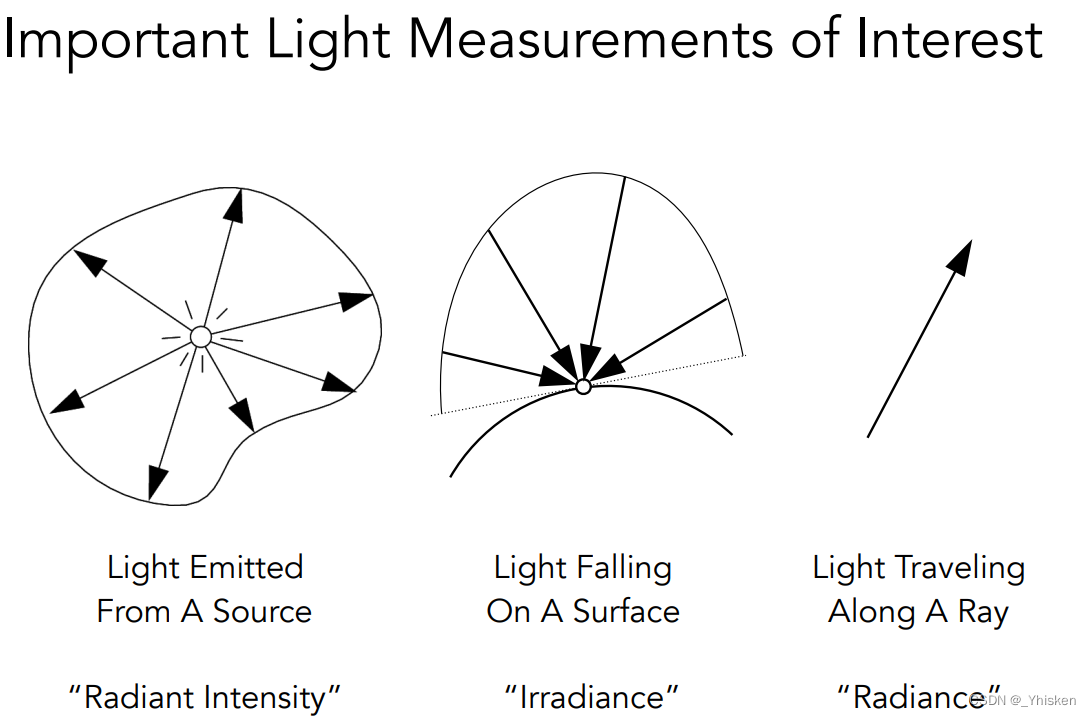
当然在辐射度量学中不止有辐射通量这一个物理量，还有很多。还有Radiant Intensity(辐射强度)，Irradiance(辐射照度/辐照度/辐射通量密度)，Radiance(辐射亮度/辐亮度)。

三、Radiant Intensity—辐射强度

1.定义

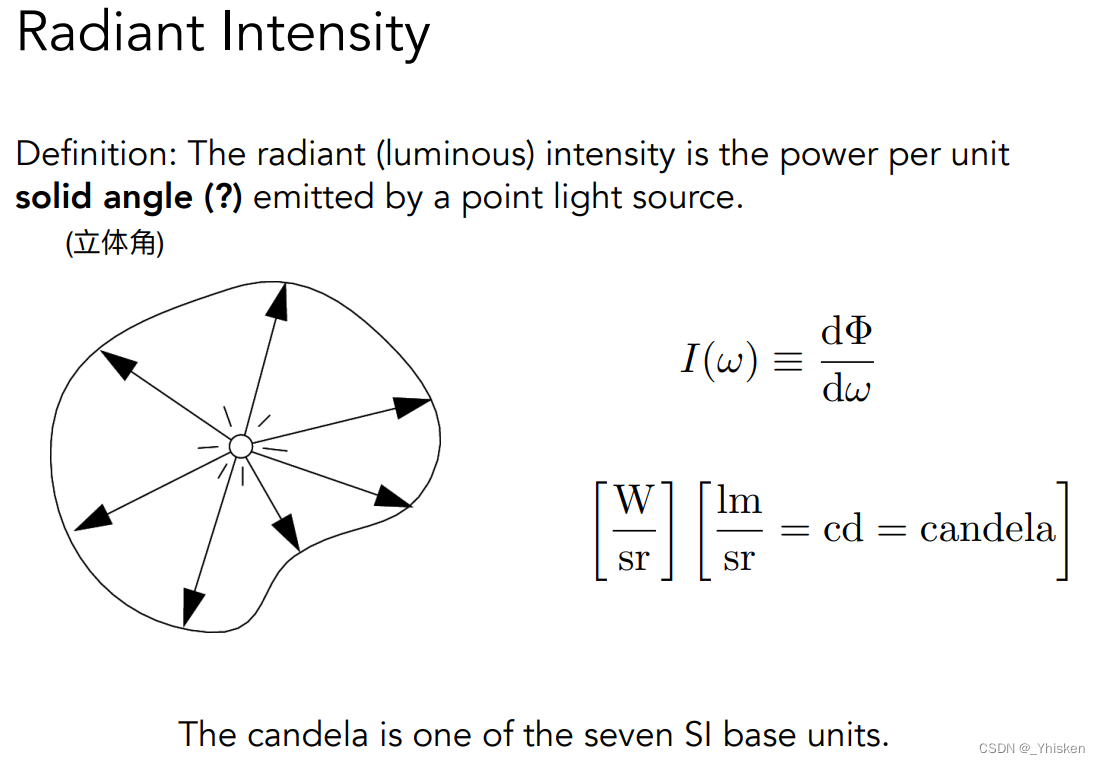
Radiant Intensity(辐射强度)：点辐射源在某方向上单位立体角内传送的辐射通量，记作I，即I(ω)=dΦe/dΩ，也就是说用单位辐射通量/单位立体角就是辐射强度。当然如果不是辐射通量是功率，也就是说单位是lm的情况下，那么它得到的单位叫candela简称cd。

2.立体角

我们知道在平面几何中角的定义是用弧长l除以半径r，也就是弧度制，它很科学，因为如果圆等比例放大，那么弧长和半径也会等比例放大，那么l/r也就不变，角也就不变，这很准确。

而立体角是在二维上进行了推广，也就是球表面上的一块小面积除以r的平方得到的就是立体角。显然整个球的立体角是4π。

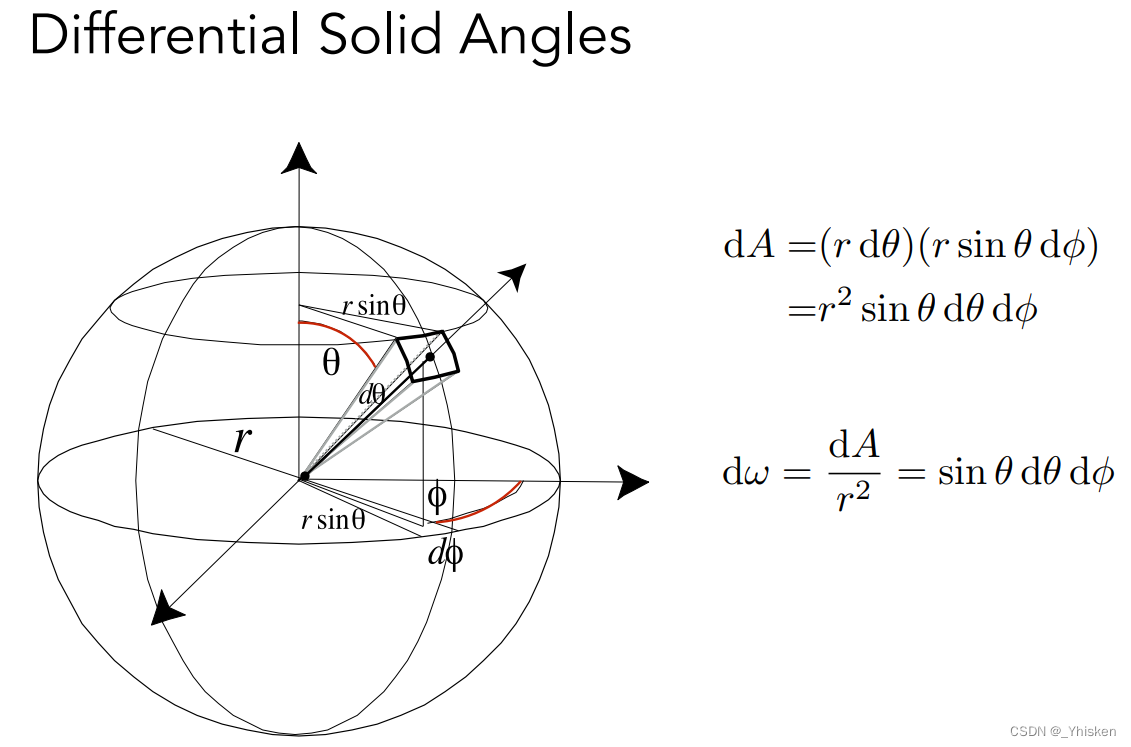
那么如何求单位立体角呢？很简单，我们在一个球坐标中去定义，我们在水平方向旋转的角度设为Φ，竖直方向旋转的角度设为θ，那么我们就可以表示球面上任何一个点。再想想立体角的定义，面积除以半径的平方，那么我们首先要把单位面积求出来(这里做了近似)，我们假定球面上的面积就是一个矩形的面积。那么就很容易得到单位面积dA=(r·dθ)(r·sinθ·dΦ)。求出之后再除以r的平方就得到单位立体角dω=sinθ·dθ·dΦ。

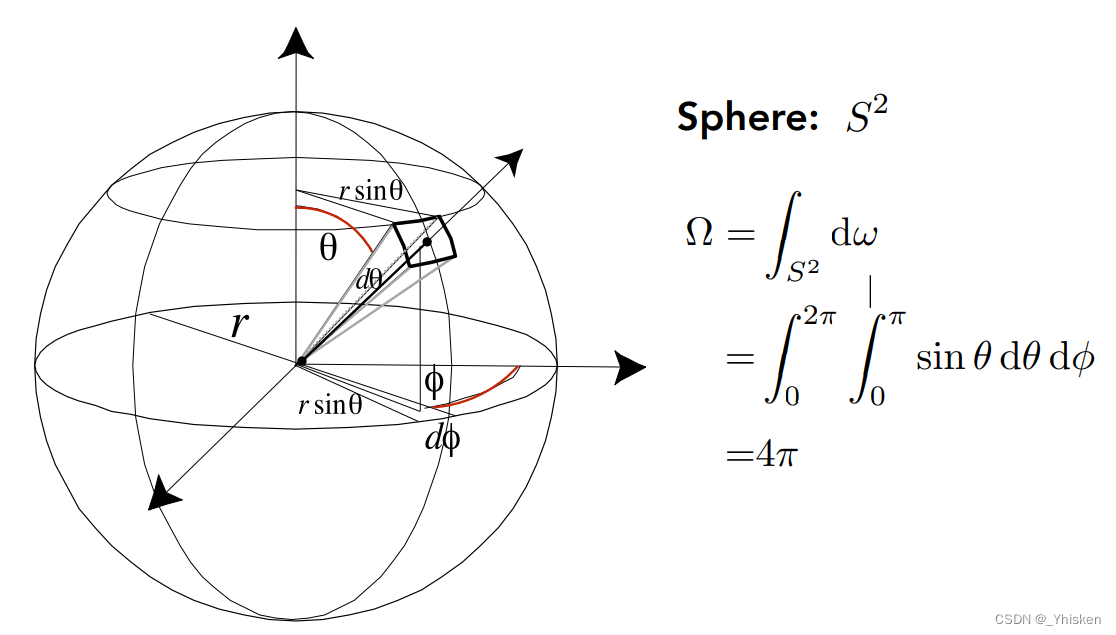
而显然的，如果我们对整个球的各个方向单位立体角做一个积分，得到的就是整个球的立体角也就是4π。

3.小结

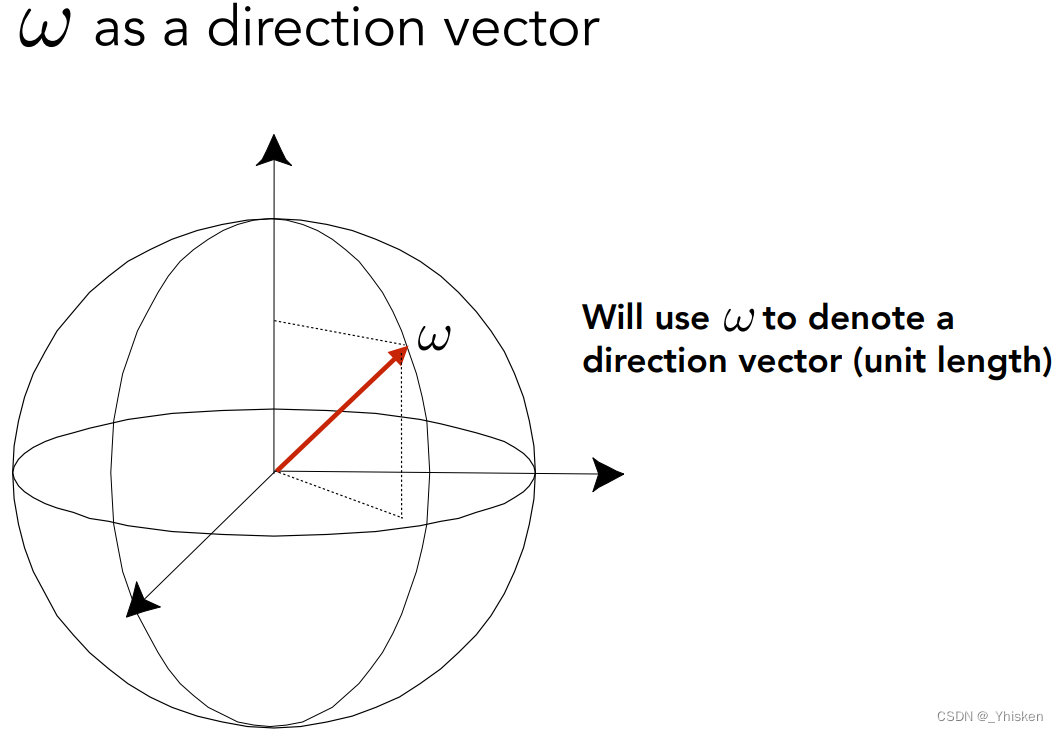
前面说明了，我们在空间中可以用 ω 这个方向向量表示空间中任何一个方向，并且可以把它写成(θ,Φ)，并且我们还可以求出它的立体角，通过这种定义会有利于许多我们后面的计算和理解。

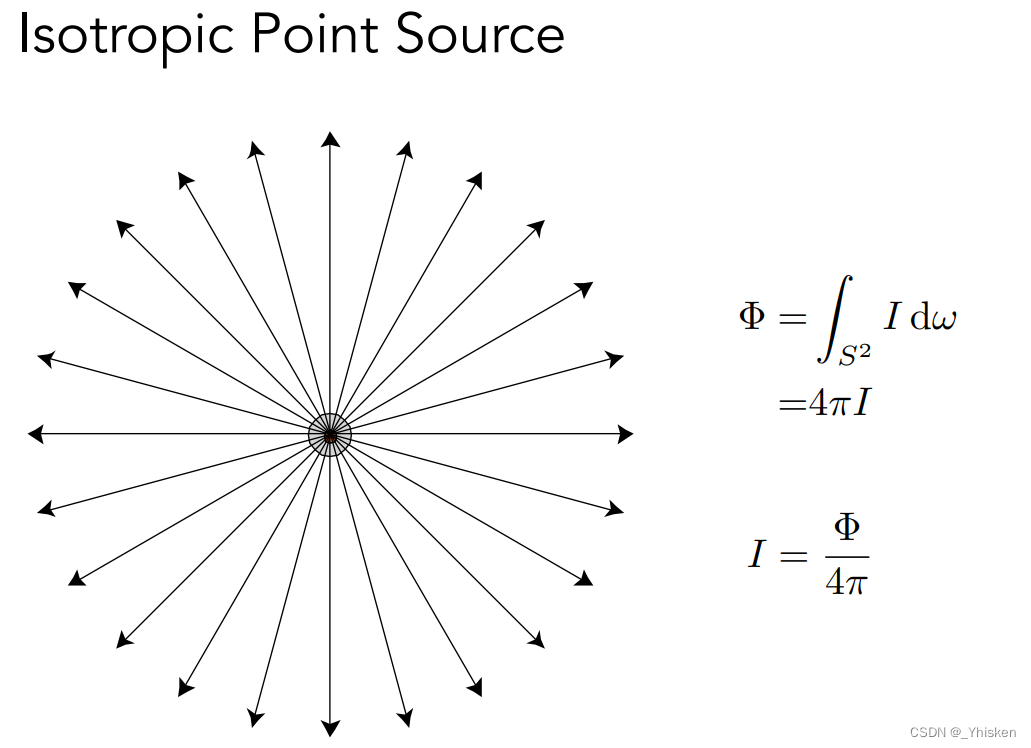
而对于一个点光源，我们定义了它的辐射通量之后就可以利用我们之前说到的公式求出这个光源的Radiant Intensity(辐射强度)，这也表示，辐射强度实际上就是在任何一个方向上的辐射通量。

也就是说，当我们有一个均匀向四周发射光线的光源，我们完全可以用它的辐射通量Φ除以它的整个立体角4π，进而得到它任何一个方向上的Intensity，也就是辐射强度。

四、Irradiance—辐照度

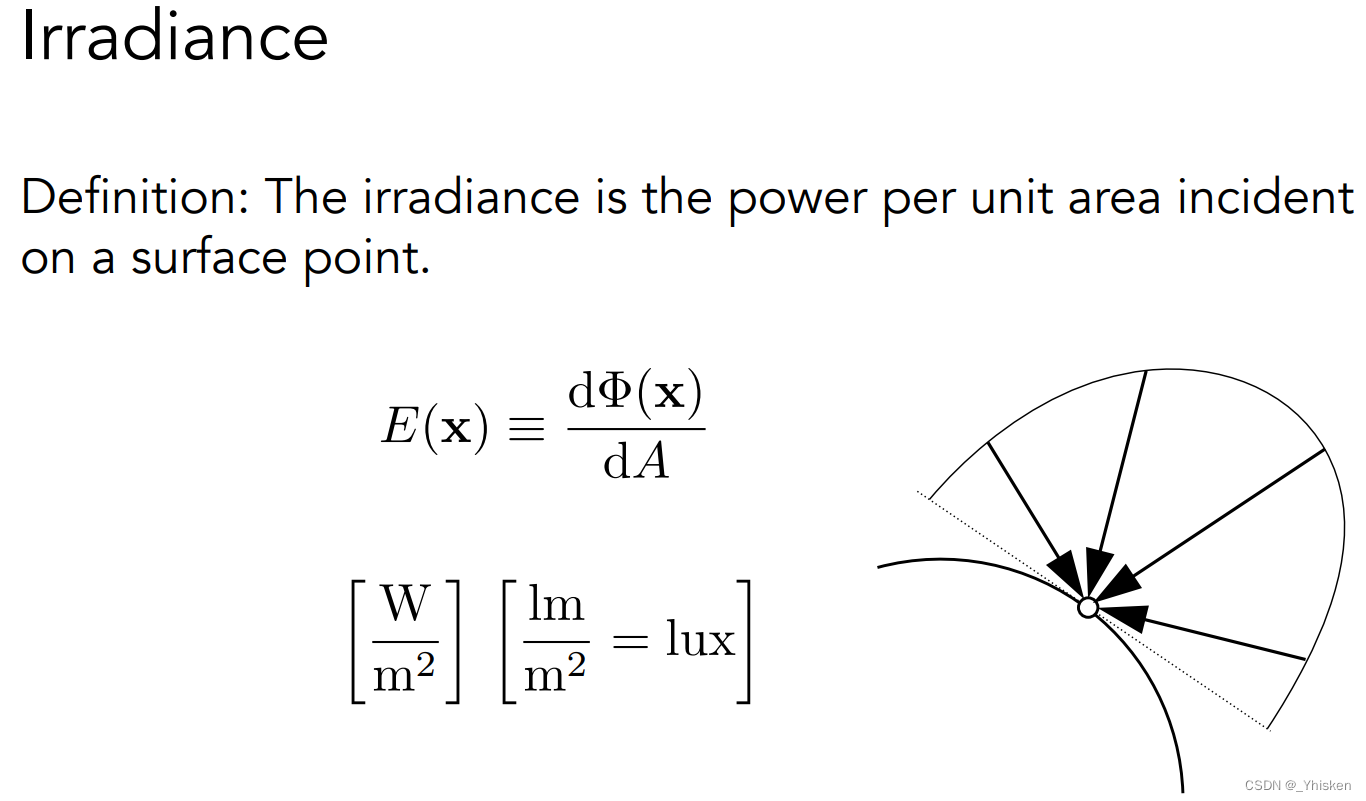
Irradiance，辐照度又称辐射照度，是受照面单位面积上的辐射通量，单位：瓦每平方米(W/㎡)。当然和Radiant Intensity相同，Irradiance也有流明与之对应的单位，是lux。

从某种意义上来说，它描述了光能量在单位面积上的分布情况，是所有方向上的Intensity的加权平均值，其中权重是入射光线在单位面积上的投影面积所对应的立体角。而Irradiance本身不具有方向性。

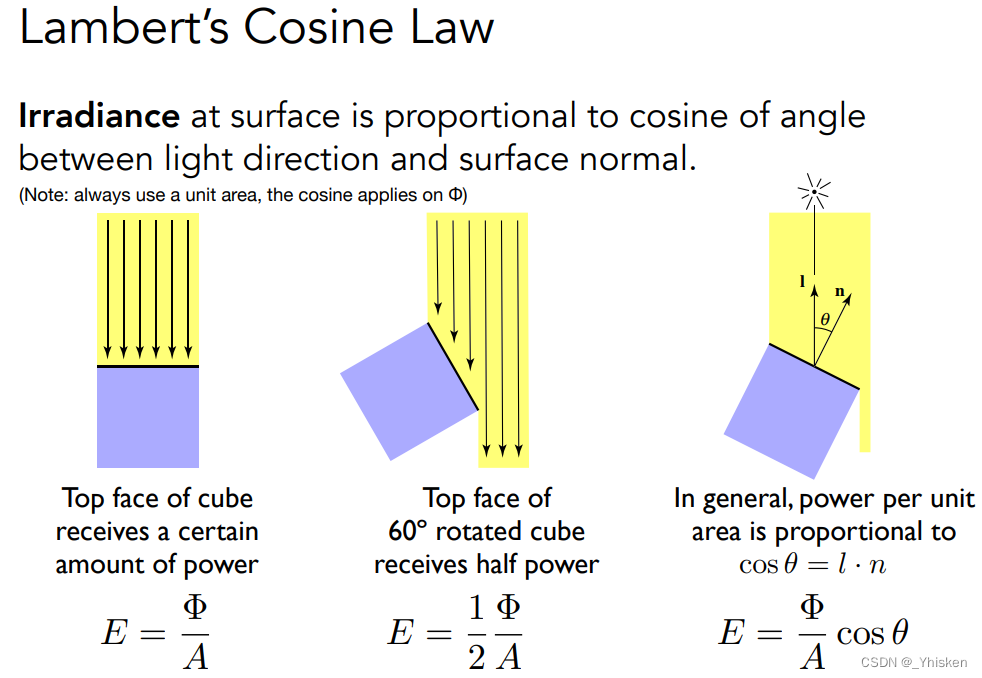
那么这里单位受照面的单位面积和我们之前提到的Lambert的规定类似，我们在这里规定的面积也要垂直于光线的方向，才能直接除以它的受照单位面积，否则要乘以cosθ。

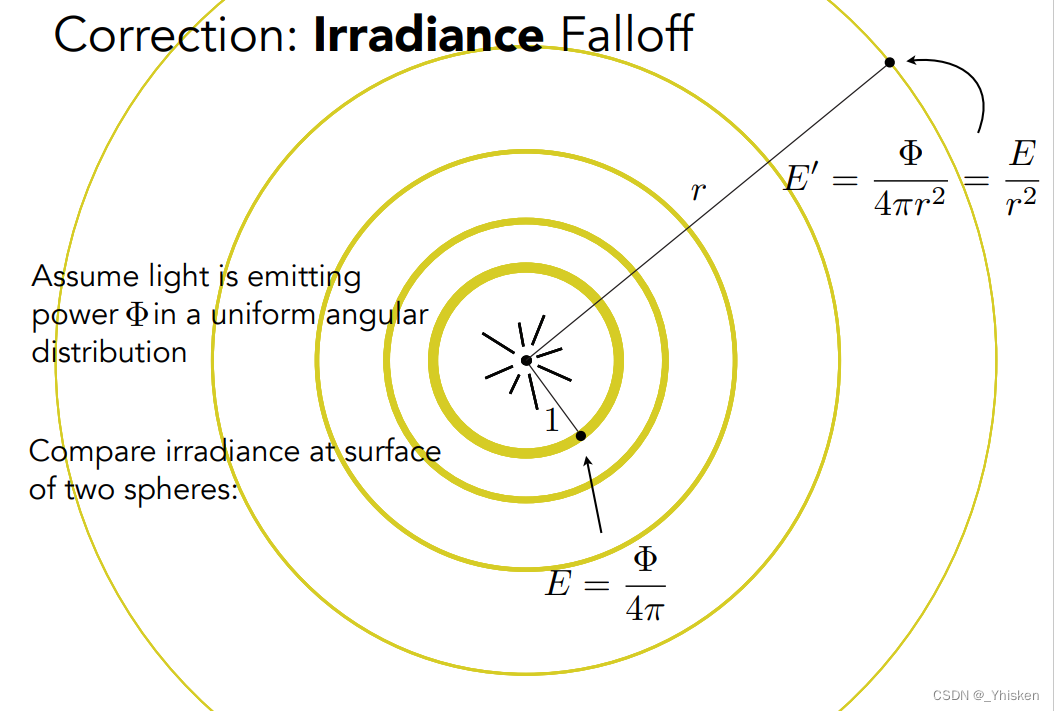
与此同时，通过Irradiance，我们可以对我们之前的光线衰减做出一个更好的理解，我们之前说想象光线四周发出均匀的分布在各个球壳上，而随着光传播距离越来越远，球壳面积越来越大，单位面积上分布的能量也就和r的平方成反比。这里的“能量”也就是Irradiance。而每个球壳上单位面积吸收的Irradiance也正是由辐射通量Φ除以球的表面积得到的，这也正是和r的平方成反比。

五、Radiance——辐亮度

Radiance，辐射亮度简称辐亮度。单位( $\bg_white \textbf{W/sr*m}^{2}{\color{Yellow} }{\color{Red} {\color{Yellow} }}$ )，表示面辐射源上某点在一定方向上的辐射强弱的物理量。指面辐射源在单位时间内通过垂直面元法线方向n上单位面积、单位立体角上辐射出的能量，即辐射源在单位投影面积上、单位立体角内的辐射通量。

简单的说，我们考虑dA(单位面积)接收的能量，当以某一个单位立体角方向ω辐射出去，这个方向的能量是多少，就是Radiance。

与Intensity和Irradiance不同的是，Radiance做了两次微分，既对单位立体角求微分又对单位面积求微分。那我们可以换一种思路，可以把Radiance理解为单位立体角下的Irradiance，或者理解成单位面积下的Intensity。

1.Incident Radiance—入射辐亮度

而根据上面的定义，单位立体角下的Irradiance可以有一个更形象的描述：Incident Radiance，入射辐照度，如上面的，Irradiance是指dA接收到的四面八方不同方向的能量，而把它再除以单位立体角，也就是只考虑从某一个方向进到dA的能量被dA吸收了多少，也就是Incident Radiance。

2.Exiting Radiance—出射辐亮度

同样的，我们可以定义一个出射辐亮度，也就是Exiting Radiance，我们定义的dA上有很多的Intensity，而我们只考虑众多Intensity中朝某一个立体角方向的Intensity就是Radiance。

3.Irradiance和Radiance

而我们常用的通常是Irradiance和Radiance的互相转化，我们前面讲到了，两者相差的仅仅是方向性，对于任意一点p，它的Radiance就是从某个立体角方向进入的Irradiance，也就是dE，而如果把dE做一个积分就会得到它从单位半球接受的所有Iradiance，也就是E(Power/Flux)。

五、Bidirectional Reflectance Distribution Function(BRDF)—双向反射分布函数

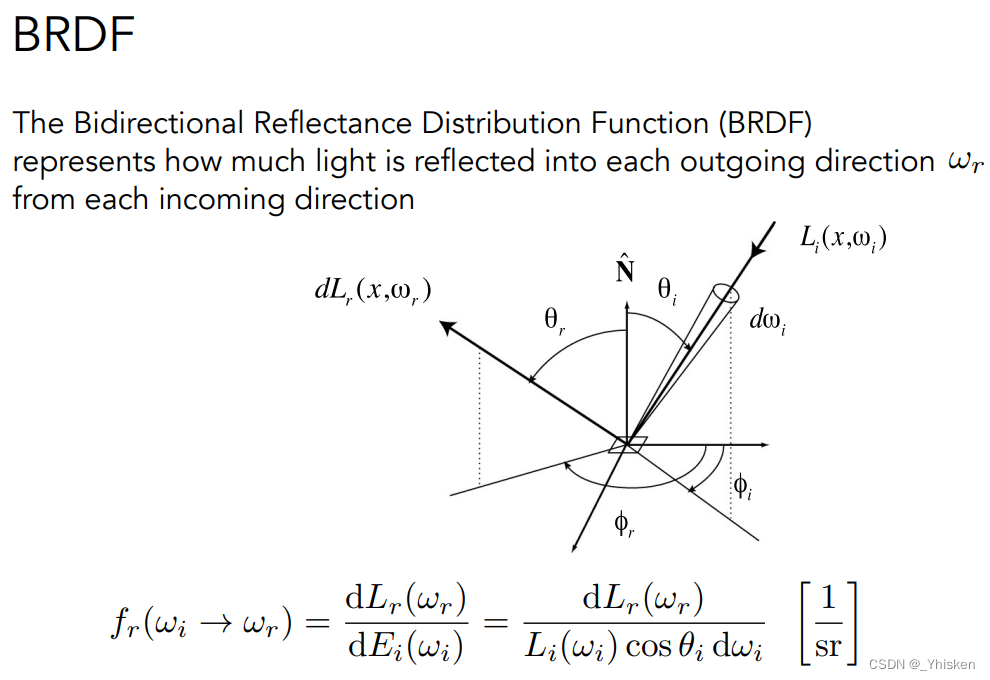
BRDF，也就是双向反射分布函数，BRDF定义了：在一块单位面积从某一个立体角方向上接收的所有Radiance，也就是我们之前所说的Irradiance，它对于块单位面积反射出去的Radiance的贡献度是多少。简单地说就是用发射出去的Radiance去除以接收的Irradiance得到的一个比值。

也就是说我们可以换一种方式理解反射，之前我们可以理解成在一个点，光线的方向被改变了。现在我们可以理解成，这个点把光的能量吸收了，然后又向另一个方向发射了出去。而实际上BRDF定义了不同的材质，也就是说不同的材质的BRDF中的所谓“贡献度”是不同的，也就导致了不同的材质与光线作用的不同。

1.Reflection Equation反射方程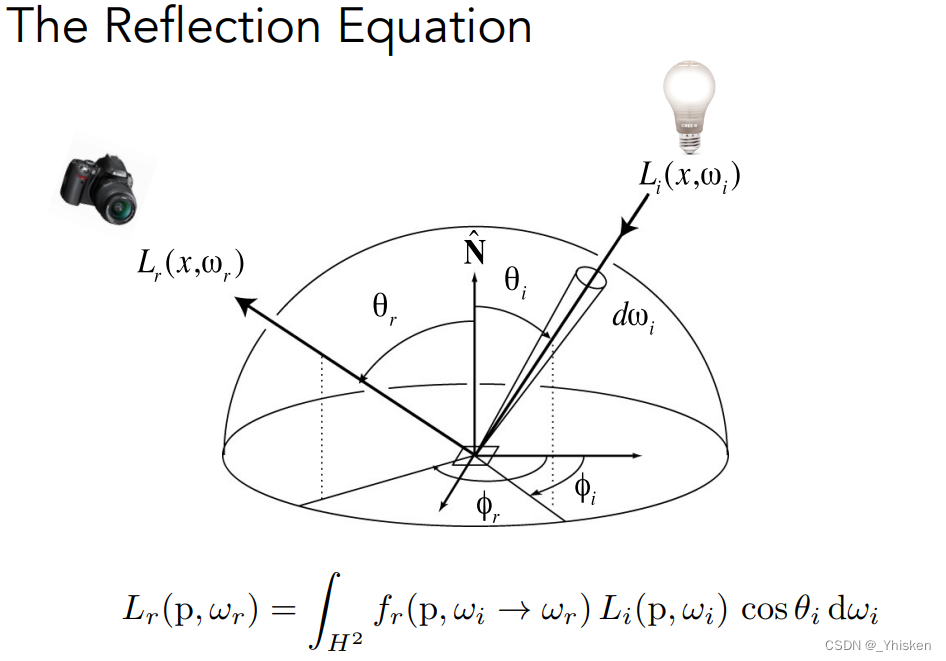

而通过BRDF，我们可以得到一个反射方程，也很好理解，我们前面说的Irradiance是某一个立体角方向发射而来并被接收的，那么我们对它做一个积分，就可以得到所有立体角方向射过来并被接收到的Irradiance也就是我们前面提到的Flux/Power，再乘以我们的BRDF，我们就可以得到最终吸收了每一个立体角方向光线的能量然后从某一个方向反射出来的这个Radiance是多少。

简单地说，反射方程定义了一个着色点接受了环境中的辐射通量后，从反射方向看去，它反射出的样子，也就是我们所说的Radiance(辐亮度)。

2.Rendering Equation—渲染方程

我们之前通过反射方程定义了我们会从反射方向得到的Radiance，然而，实际情况中物体可能会有自发光，那怎么办呢？很简单，只要把这部分自发光的Radiance加上就可以了，而加上之后就得到了我们的渲染方程如上图，它可以描述所有情况的光线传播。

3.对渲染方程的理解

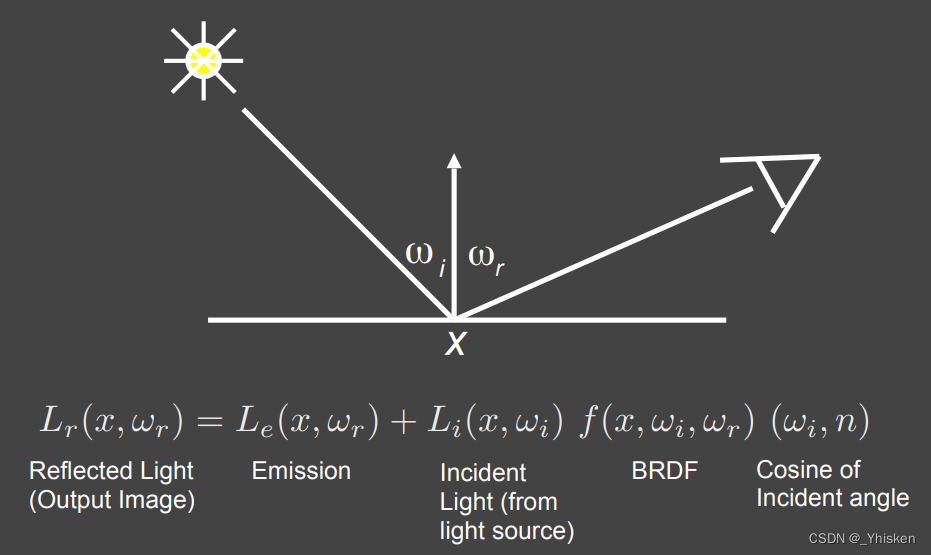
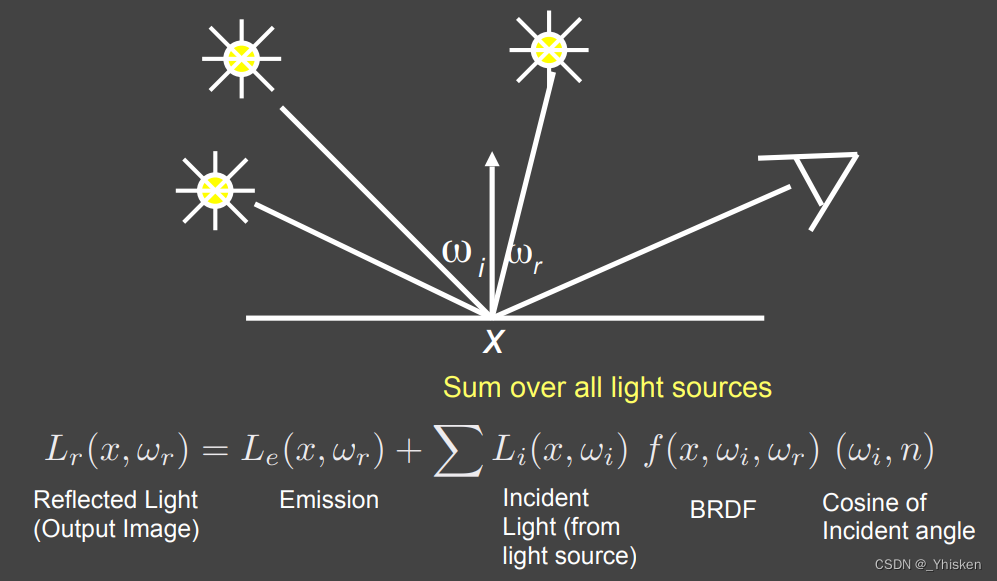
我们先来看建立在只有一个/多个点光源的基础上的渲染方程，很简单，如上图，我们对所有点光源的BRDF项求和即可，这也符合我们如果开得灯越多就越亮的生活常识。

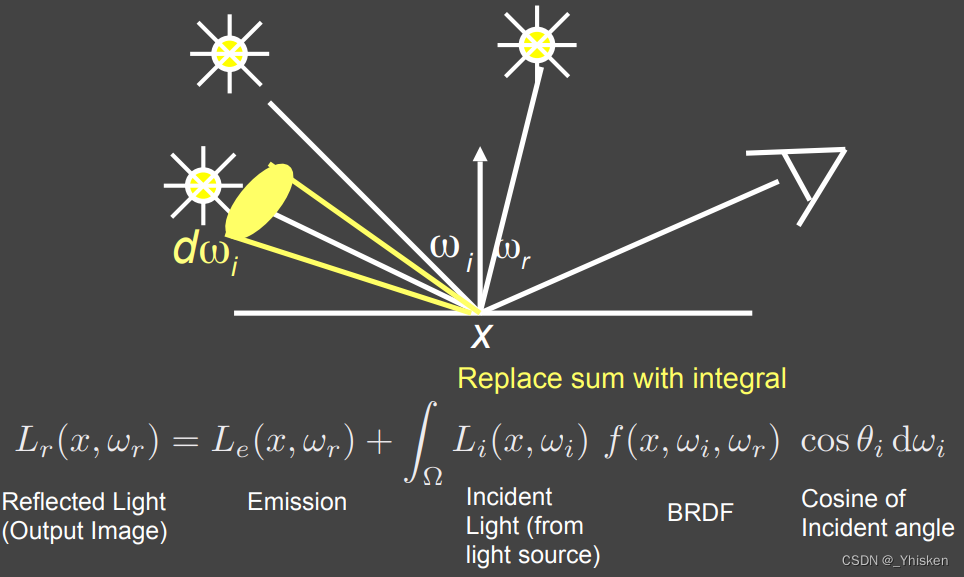
接下来我们考虑有面光源的情况，对于面光源我们可以把它想象为一堆点光源的集合，然后我们同样计算它们从反射方向发出的Radiance。这样，BRDF项的求和就变成了积分。

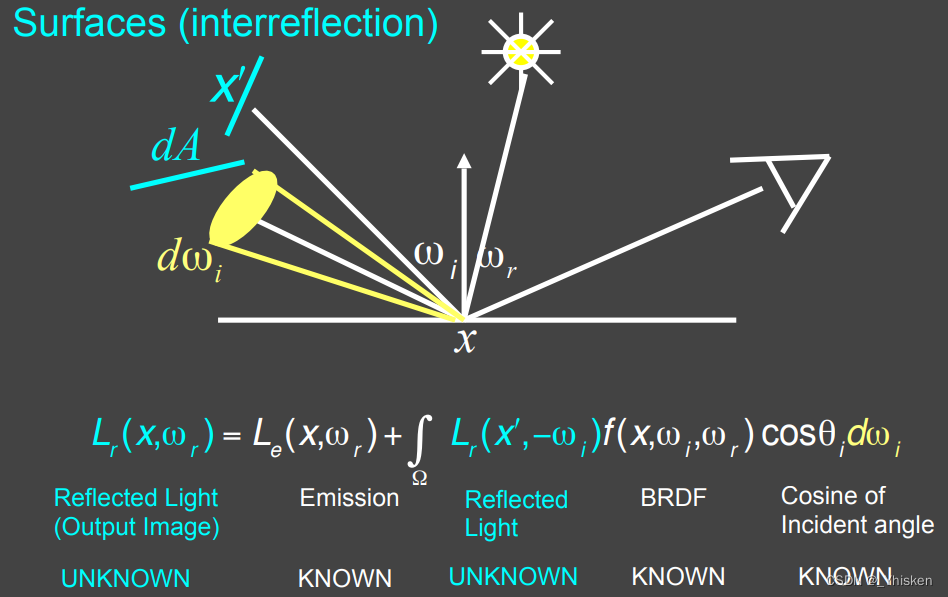
当然，我们之前考虑的都是光源的直接光照的影响，在环境中还有一些其它的东西，它们会反射光源的光，然后同样影响我们看到的点。而实际上，无论是间接光源还是直接光源，我们都可以把它当成环境中影响x点的众多Radiance中的其中一个，也就是本质上来说，它们并没有区别。

而回过头来看，在整个渲染方程中，只有两个量我们不知道，一个是最终的结果，另一个则是各个反射出的Radiance。而其它的，如自发光，BRDF，夹角，在场景中我们都可以得到或定义好。那么我们就可以简化一步，得到简化后的渲染方程，u代表我们看到的方向，也就是反射方向，v代表入射方向，e代表自发光，l则代表Radiance，K则是反射操作符。

我们最后简化可以简化成一个极简的形式：L=E+KL(这里面涉及到线性代数的知识)，这也就代表着，我们看一个点发出的能量等于它自己发出的能量和经过该点反射出来的能量。在L=E+KL的表达式中，左边的L表示表面点x处的辐射强度，右边的L表示从其他表面点处发射的光线打到x处的辐射强度，并不是同一个物理量。

而写成L=E+KL的形式之后，移项，虽然(I-K)的逆是一个矩阵，但我们也可以进一步变换变成级数展开的一种形式。(实际上，将渲染方程中的L = E + KL转换成(I - K)L = E的过程中，我们并没有将两个不同的物理量合并成一个。相反，我们是将表面点x处的辐射强度L(x,ωo)拆分成了两个部分：一部分是从表面点x处沿着方向ωo发射的光线的辐射强度，另一部分则是从其他表面点处发射的光线到达表面点x处的辐射强度。

在将L = E + KL转换成(I - K)L = E的过程中，我们是将KL看作一个线性算子，它将L映射到从其他表面点处发射的光线到达表面点x处的辐射强度。因此，(I - K)L表示表面点x处的辐射强度中减去了从其他表面点处发射的光线到达表面点x处的辐射强度的贡献。这样，我们就可以使用蒙特卡罗方法来估计(I - K)L的值，从而得到表面点x处的辐射强度L。)

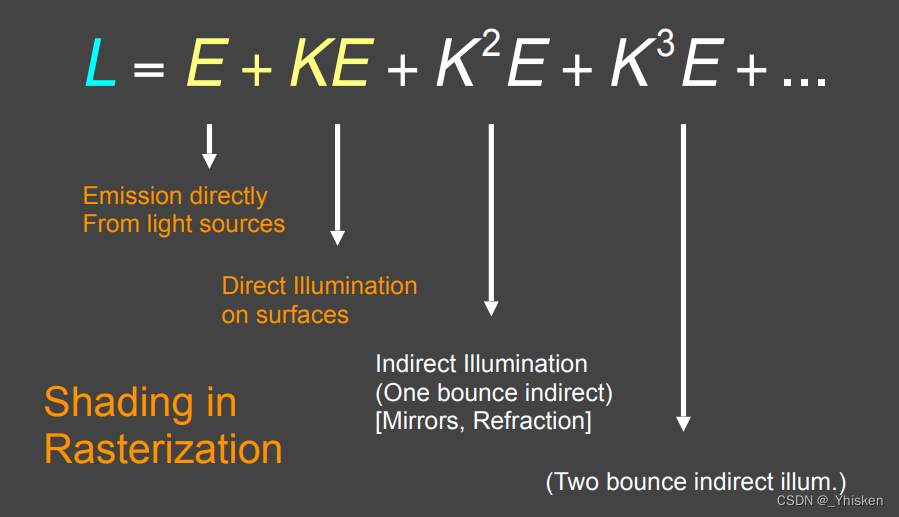
最终我们得到了一个级数展开的渲染方程，其中，E表示直接光照和自发光的贡献，K表示从其他表面点处发射的光线到达表面点x处的辐射强度。K^2表示从其他表面点处反射或折射两次到达表面点x处的辐射强度，K^3表示从其他表面点处反射或折射三次到达表面点x处的辐射强度，以此类推。

这个级数表示了所有可能的光线路径对辐射强度的贡献，包括直接光照和自发光、一次反射和折射、两次反射和折射、三次反射和折射等等。这个级数中的每一项都可以使用类似于KL的积分形式来计算。而在实际应用中，我们通常只考虑级数中的前几项，因为随着反射和折射次数的增加，光线路径的数量呈指数级增长，计算量会变得非常大。因此，我们需要根据场景的复杂程度和渲染质量的要求来选择级数的截断点。

这样我们就可以理解全局光照了，全局光照，那也就是直接光照和间接光照的集合。

而我们回顾光栅化，它只做了自发光E，和光线弹射一次KE的部分。

六、总结

那么到这，从辐射度量学的各个物理量，到BRDF再到渲染方程就都介绍完毕了，这么一套流程是路径追踪和PBR流程的基础，它在工业界非常实用，用于描述真实的物理世界和真实感的渲染，许多画面精美的电影都离不开这些东西。当然，想要彻底理解这个事情是比较困难的，我也花了很长时间，在GAMES101中我理解时间最长的就是路径追踪这块，其次就是MVP变换和光场，当然“消除恐惧的最好办法就是面对恐惧，微笑着面对它”，所以我还是建议花大量的时间来琢磨它争取彻底把它弄清楚，这无关别的，因为真的弄懂了某件事之后，得到的快乐是很大的，它比一时之快更快乐，因为：“真理的味道，是甜的。”