回溯算法专题
- 框架篇
- 全排列问题
- N 皇后问题
- 如果只需要一个合法答案,怎么办?
- 快速排序
- LeetCode 912. 排序数组
- 解题思路
- 代码实现
- LeetCode 215. 数组中的第K个最大元素
- 解题思路
- 代码实现
- 总结
不要纠结,干就完事了,熟练度很重要!!!多练习,多总结!!!
框架篇
直接上回溯算法框架。解决一个回溯问题,实际上就是一个决策树的遍历过程。你只需要思考 3 个问题:
- 路径:也就是已经做出的选择。
- 选择列表:也就是你当前可以做的选择。
- 结束条件:也就是到达决策树底层,无法再做选择的条件。
result = []
def backtrack(路径, 选择列表):
if 满足结束条件:
result.add(路径)
return
for 选择 in 选择列表:
做选择
backtrack(路径, 选择列表)
撤销选择
其核心就是 for 循环里面的递归,在递归调用之前「做选择」,在递归调用之后「撤销选择」。
全排列问题
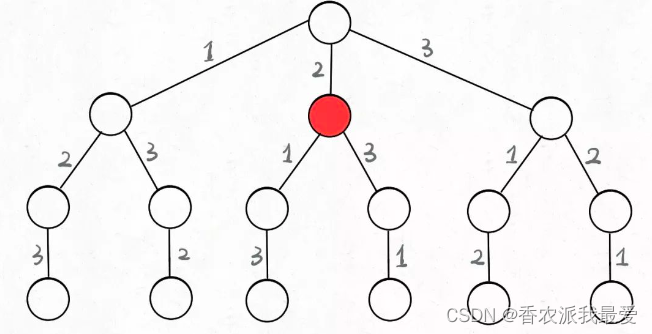
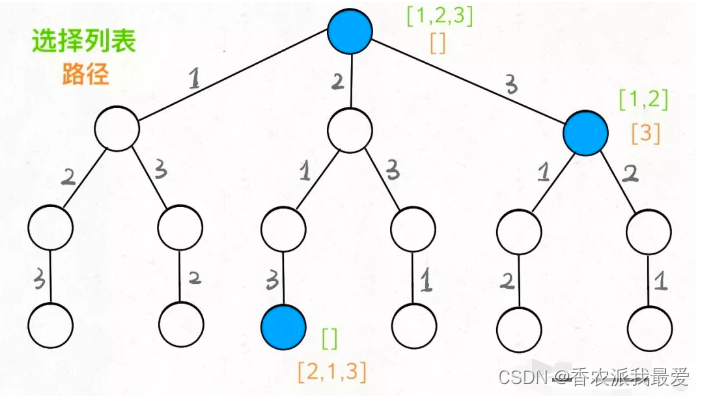
不妨把这棵树称为回溯算法的「决策树」。为啥说这是决策树呢,因为你在每个节点上其实都在做决策。
可以选择 1 那条树枝,也可以选择 3 那条树枝。为啥只能在 1 和 3 之中选择呢?因为 2 这个树枝在你身后,这个选择你之前做过了,而全排列是不允许重复使用数字的。
现在可以解答开头的几个名词:[2]就是「路径」,记录你已经做过的选择;[1,3]就是「选择列表」,表示你当前可以做出的选择;「结束条件」就是遍历到树的底层,在这里就是选择列表为空的时候。
如果明白了这几个名词,可以把「路径」和「选择列表」作为决策树上每个节点的属性,比如下图列出了几个节点的属性:
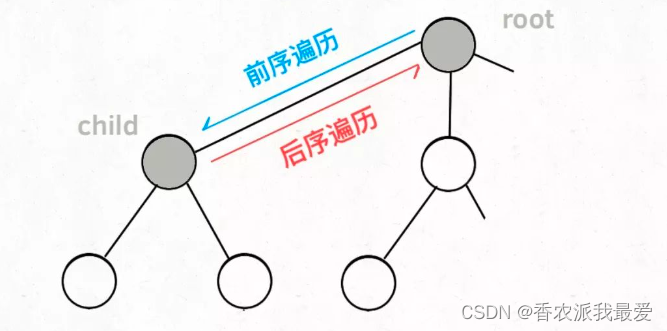
前序遍历的代码在进入某一个节点之前的那个时间点执行,后序遍历代码在离开某个节点之后的那个时间点执行。
回想我们刚才说的,「路径」和「选择」是每个节点的属性,函数在树上游走要正确维护节点的属性,那么就要在这两个特殊时间点搞点动作:
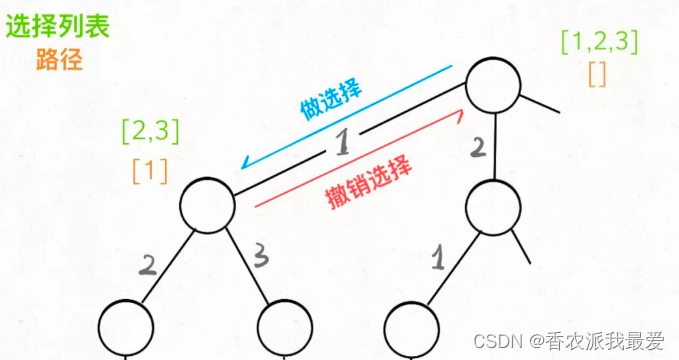
List<List<Integer>> res = new LinkedList<>();
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
// 记录「路径」
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return res;
}
// 路径:记录在 track 中
// 选择列表:nums 中不存在于 track 的那些元素
// 结束条件:nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList<Integer> track) {
// 触发结束条件
if (track.size() == nums.length) {
res.add(new LinkedList(track));
return;
}
for (int i = 0; i < nums.length; i++) {
// 排除不合法的选择
if (track.contains(nums[i]))
continue;
// 做选择
track.add(nums[i]);
// 进入下一层决策树
backtrack(nums, track);
// 取消选择
track.removeLast();
}
}
必须说明的是,不管怎么优化,都符合回溯框架,而且时间复杂度都不可能低于 O(N!),因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点,不像动态规划存在重叠子问题可以优化,回溯算法就是纯暴力穷举,复杂度一般都很高。
N 皇后问题
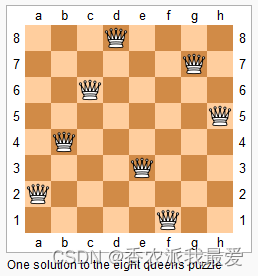
给你一个 N×N 的棋盘,让你放置 N 个皇后,使得它们不能互相攻击。
(皇后可以攻击同一行、同一列、左上左下右上右下四个方向的任意单位)
vector<vector<string>> res;
/* 输入棋盘边长 n,返回所有合法的放置 */
vector<vector<string>> solveNQueens(int n) {
// '.' 表示空,'Q' 表示皇后,初始化空棋盘。
vector<string> board(n, string(n, '.'));
backtrack(board, 0);
return res;
}
// 路径:board 中小于 row 的那些行都已经成功放置了皇后
// 选择列表:第 row 行的所有列都是放置皇后的选择
// 结束条件:row 超过 board 的最后一行
void backtrack(vector<string>& board, int row) {
// 触发结束条件
if (row == board.size()) {
res.push_back(board);
return;
}
int n = board[row].size();
for (int col = 0; col < n; col++) {
// 排除不合法选择
if (!isValid(board, row, col))
continue;
// 做选择
board[row][col] = 'Q';
// 进入下一行决策
backtrack(board, row + 1);
// 撤销选择
board[row][col] = '.';
}
}
/* 是否可以在 board[row][col] 放置皇后? */
bool isValid(vector<string>& board, int row, int col) {
int n = board.size();
// 检查列是否有皇后互相冲突
for (int i = 0; i < n; i++) {
if (board[i][col] == 'Q')
return false;
}
// 检查右上方是否有皇后互相冲突
for (int i = row - 1, j = col + 1;
i >= 0 && j < n; i--, j++) {
if (board[i][j] == 'Q')
return false;
}
// 检查左上方是否有皇后互相冲突
for (int i = row - 1, j = col - 1;
i >= 0 && j >= 0; i--, j--) {
if (board[i][j] == 'Q')
return false;
}
return true;
}
函数backtrack依然像个在决策树上游走的指针,每个节点就表示在board[row][col]上放置皇后,通过isValid函数可以将不符合条件的情况剪枝:
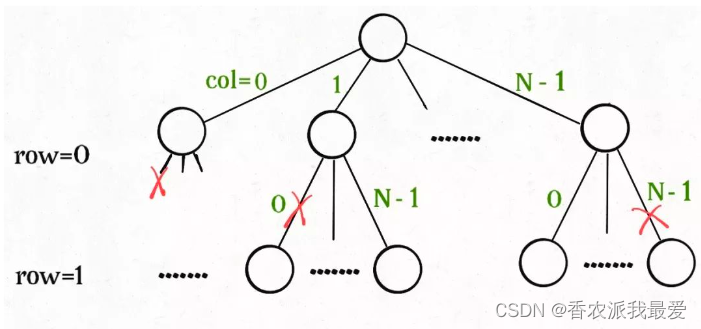
如果只需要一个合法答案,怎么办?
// 函数找到一个答案后就返回 true
bool backtrack(vector<string>& board, int row) {
// 触发结束条件
if (row == board.size()) {
res.push_back(board);
return true;
}
...
for (int col = 0; col < n; col++) {
...
board[row][col] = 'Q';
if (backtrack(board, row + 1))
return true;
board[row][col] = '.';
}
return false;
}
快速排序
LeetCode 912. 排序数组

解题思路
快速排序是先将一个元素排好序,然后再将剩下的元素排好序。
快速排序的核心无疑是 partition 函数, partition 函数的作用是在 nums[lo…hi] 中寻找一个分界点 p,通过交换元素使得 nums[lo…p-1] 都小于等于 nums[p],且 nums[p+1…hi] 都大于 nums[p]。
从二叉树的视角,我们可以把子数组 nums[lo…hi] 理解成二叉树节点上的值,srot 函数理解成二叉树的遍历函数。参照二叉树的前序遍历顺序。
代码实现
class Solution {
public int[] sortArray(int[] nums) {
sort(nums, 0, nums.length-1);
return nums;
}
public void sort(int[] nums, int lo, int hi){
if(lo > hi){
return ;
}
int j = partition(nums, lo, hi);
sort(nums, lo, j-1);
sort(nums, j+1, hi);
}
public int partition(int[] nums, int lo, int hi){
int pivot = nums[lo];
int i = lo+1, j = hi;
while(i <= j){
while(i < hi && nums[i] < pivot){
i++;
}
while(j > lo && nums[j] > pivot){
j--;
}
if(i >= j){
break;
}
swap(nums, i, j);
}
swap(nums, lo, j);
return j;
}
public void swap(int[] nums, int i, int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
LeetCode 215. 数组中的第K个最大元素

解题思路
二叉堆思路简单,但复杂度较高。既然是找第K大元素,按照快速排序思路 ,前序遍历思维 每次找到一个有序的分界点,根据分界点去找结果的点,最后返回即可。
题目问「第 k 个最大的元素」,相当于数组升序排序后「排名第 n - k 的元素」,为了方便表述,后文另 k’ = n - k。
如何知道「排名第 k’ 的元素」呢?其实在快速排序算法 partition 函数执行的过程中就可以略见一二。
刚说了,partition 函数会将 nums[p] 排到正确的位置,使得 nums[lo…p-1] < nums[p] < nums[p+1…hi]:
这时候,虽然还没有把整个数组排好序,但我们已经让 nums[p] 左边的元素都比 nums[p] 小了,也就知道 nums[p] 的排名了。
那么我们可以把 p 和 k’ 进行比较,如果 p < k’ 说明第 k’ 大的元素在 nums[p+1…hi] 中,如果 p > k’ 说明第 k’ 大的元素在 nums[lo…p-1] 中。
代码实现
class Solution {
public int findKthLargest(int[] nums, int k) {
k = nums.length-k;
int low = 0, high = nums.length-1;
while(low <= high){
int p = partition(nums, low, high);
if(p > k){
high = p-1;
}else if(p < k){
low = p+1;
}else{
return nums[p];
}
}
return -1;
}
public int partition(int[] nums, int low, int high){
int pivot = nums[low];
int i = low+1, j = high;
while(i <= j){
while(i < high && nums[i] < pivot){
i++;
}
while(j > low && nums[j] > pivot){
j--;
}
if(i > j){
break;
}
swap(nums, i, j);
}
swap(nums, low, j);
return j;
}
public void swap(int[] nums, int i, int j){
int tmp = nums[i];
nums[i] = nums[j];
nums[j] = tmp;
}
}
int findKthLargest(int[] nums, int k) {
// 小顶堆,堆顶是最小元素
PriorityQueue<Integer>
pq = new PriorityQueue<>();
for (int e : nums) {
// 每个元素都要过一遍二叉堆
pq.offer(e);
// 堆中元素多于 k 个时,删除堆顶元素
if (pq.size() > k) {
pq.poll();
}
}
// pq 中剩下的是 nums 中 k 个最大元素,
// 堆顶是最小的那个,即第 k 个最大元素
return pq.peek();
}
总结
本题来源于Leetcode中 归属于回溯算法类型题目。
同许多在算法道路上不断前行的人一样,不断练习,修炼自己!
如有博客中存在的疑问或者建议,可以在下方留言一起交流,感谢各位!
觉得本博客有用的客官,可以给个点赞+收藏哦! 嘿嘿
喜欢本系列博客的可以关注下,以后除了会继续更新面试手撕代码文章外,还会出其他系列的文章!