随机梯度下降法

批量梯度下降使用全部的训练样本来计算梯度，并更新模型参数，因此它的每一次迭代计算量较大，但对于凸优化问题，可以保证每次迭代都朝着全局最优解的方向前进，收敛速度较快，最终收敛到的结果也比较稳定。

随机梯度下降则每次迭代仅使用一个样本来计算梯度，并更新模型参数，因此每次迭代的计算量较小，但收敛速度较慢，最终收敛结果也不够稳定，可能会陷入局部最优解。

在实际应用中，批量梯度下降通常用于训练数据量较小、维度较高的情况，而随机梯度下降通常用于训练数据量较大、维度较低的情况。同时也可以采用一种介于两者之间的小批量梯度下降（Mini-Batch Gradient Descent），即每次迭代使用一定数量的随机样本来计算梯度，并更新模型参数，这种方法在训练大规模数据集时也比较实用。
我们用一个函数举例子：

这里需要求它的梯度：

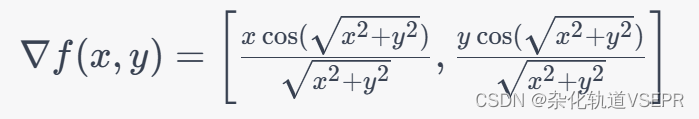
随机梯度下降法的代码实现：

import numpy as np
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
np.random.seed(42)  # 设置随机种子，保证每次运行结果相同
x = np.random.randn(100, 3)
y = x.dot(np.array([4, 5, 6])) + np.random.randn(100) * 0.1
def loss_function(w, x, y):
    return 0.5 * np.mean((np.dot(x, w) - y) ** 2)

def gradient_function(w, x, y):
    return np.dot(x.T, np.dot(x, w) - y) / len(y)
def SGD(x, y, w_init, alpha, max_iter):
    w = w_init
    for i in range(max_iter):
        rand_idx = np.random.randint(len(y))
        x_i = x[rand_idx, :].reshape(1, -1)
        y_i = y[rand_idx]
        grad_i = gradient_function(w, x_i, y_i)
        w = w - alpha * grad_i
    return w
fig = plt.figure()
ax = Axes3D(fig)
W0 = np.arange(0, 10, 0.1)
W1 = np.arange(0, 10, 0.1)
W0, W1 = np.meshgrid(W0, W1)
W2 = np.array([SGD(x, y, np.array([w0, w1, 0]), 0.01, 1000)[2] for w0, w1 in zip(np.ravel(W0), np.ravel(W1))])
W2 = W2.reshape(W0.shape)
ax.plot_surface(W0, W1, W2, cmap='coolwarm')
ax.set_xlabel('w0')
ax.set_ylabel('w1')
ax.set_zlabel('loss')
plt.show()

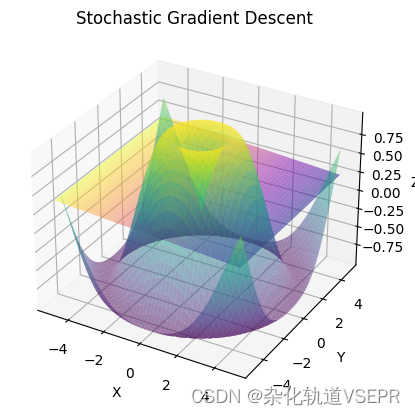
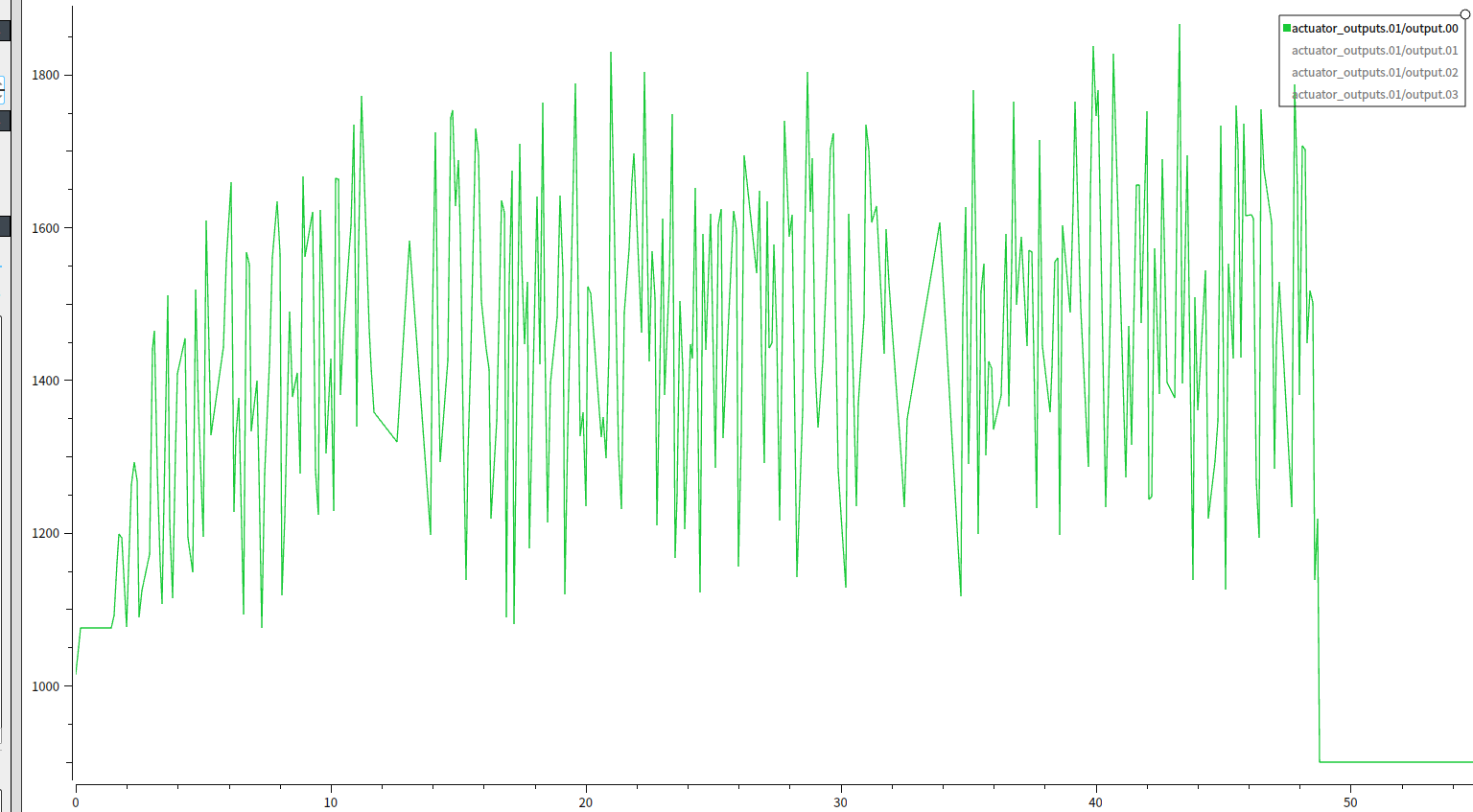
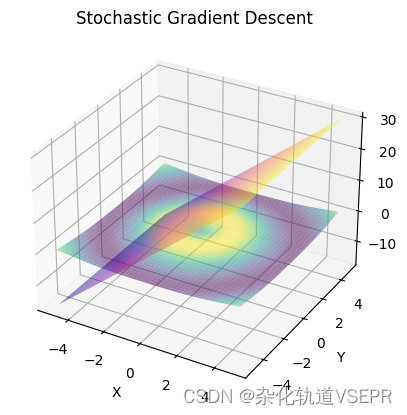
这个图像表示了随机梯度下降算法在二元线性回归问题中对于不同初始权重（$x$，$y$）的收敛情况。横轴和纵轴分别表示$x$和$y$的值，而竖轴表示算法收敛的迭代次数。不同颜色的曲面表示不同的收敛路径。可以看到，算法在不同的初始权重下都能收敛到大致相同的最优权重，这也验证了随机梯度下降算法的鲁棒性和适用性。此外，可以看到不同初始权重下的收敛速度和路径都不同，这也说明了随机梯度下降算法的随机性。
可以更换max_iter的值，以下是迭代10000此的结果：

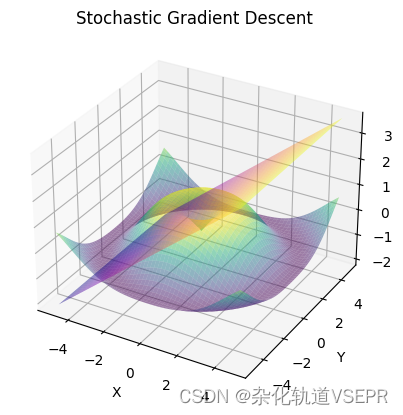
迭代100000的结果：

在这段代码中的数学含义代表如下：

w_init：表示模型参数的初始值。这里是一个一维数组，包含三个元素，分别对应截距、x1系数和x2系数。

x：表示输入特征矩阵，每行包含两个特征x1和x2。

y：表示输出标签，是一个一维数组。

alpha：表示学习率，是一个超参数，决定了每一次迭代参数的更新幅度。

max_iter：表示最大迭代次数，也是一个超参数。

rand_idx = np.random.randint(len(y))：在每一次迭代中，随机选择一个样本。

x_i = x[rand_idx, :].reshape(1, -1)：根据随机选择的样本索引，选取相应的特征向量，并将其变为一个1行2列的矩阵。

y_i = y[rand_idx]：根据随机选择的样本索引，选取相应的输出标签。

grad_i = gradient_function(w, x_i, y_i)：计算该样本的梯度。

w = w - alpha * grad_i：更新模型参数。

return w：返回最终权重。

x = np.insert(x, 0, 1, axis=1)：将截距添加到输入特征矩阵x的第一列。

np.dot(x, w)：计算模型的预测值。

np.dot(x, w) - y：计算模型预测值与真实标签的误差。

np.dot(x.T, np.dot(x, w) - y)：计算误差的梯度。

len(y)：计算样本的数量。

return np.dot(x.T, np.dot(x, w) - y) / len(y)：返回梯度。