1.题目链接：

216. 组合总和 III

2.解题思路：

2.1.题目要求：

给一个元素数量k和一个元素和n，要求从范围[1,2,3,4,5,6,7,8,9]中返回所有元素数量为k和元素和为n的组合。（每个数字只能使用一次）

比如输入k=3，n=7，得[1,2,4]

2.2.思路：

模拟成一个n叉树，用for循环里递归的方式，完成层层遍历，终止条件变成满足元素数量为k和元素和为n就返回就好了。

2.3.回溯三部曲：

2.3.1.确定递归函数参数

需要一维数组path来存放符合条件的结果，二维数组result来存放结果集。

vector<vector<int>> result; // 存放结果集
vector<int> path; // 符合条件的结果

接下来还需要如下参数：

• targetSum（int）目标和，也就是题目中的n。
• k（int）就是题目中要求k个数的集合。
• sum（int）sum在单层搜索中可以积攒path的和，用于终止条件和targetSun作对比，看看满不满足条件
• startIndex（int）为下一层for循环搜索的起始位置。

vector<vector<int>> result;
vector<int> path;
void backtracking(int targetSum, int k, int sum, int startIndex)

2.3.2.确定终止条件

满足元素数量为k和元素和为n就返回，这里有个隐藏起来的操作，sum不等于targeSum会直接返回。

if (path.size() == k) {
    if (sum == targetSum) result.push_back(path);
    return; // 如果path.size() == k 但sum != targetSum 直接返回
}

2.3.3.单层搜索的过程

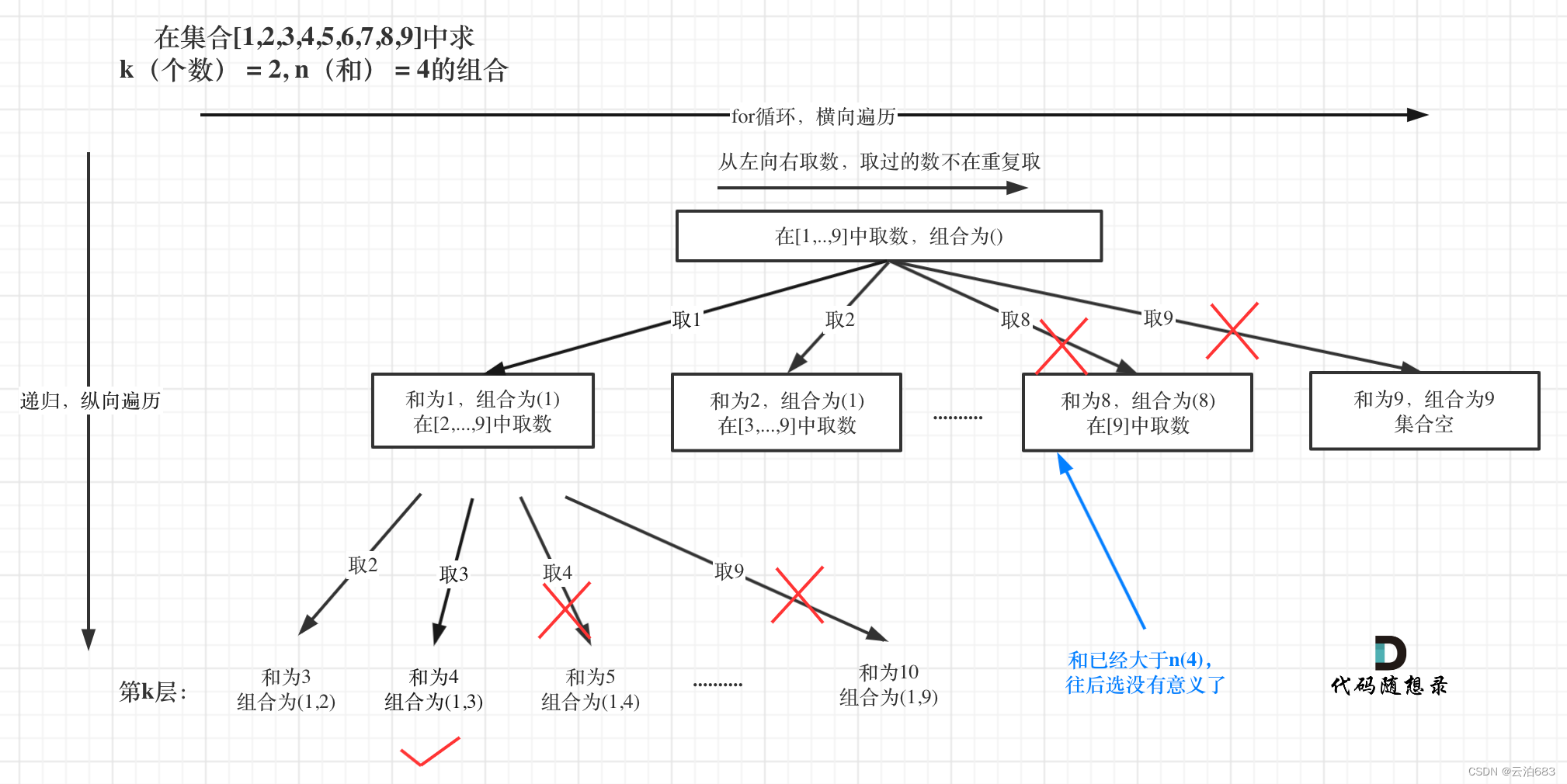
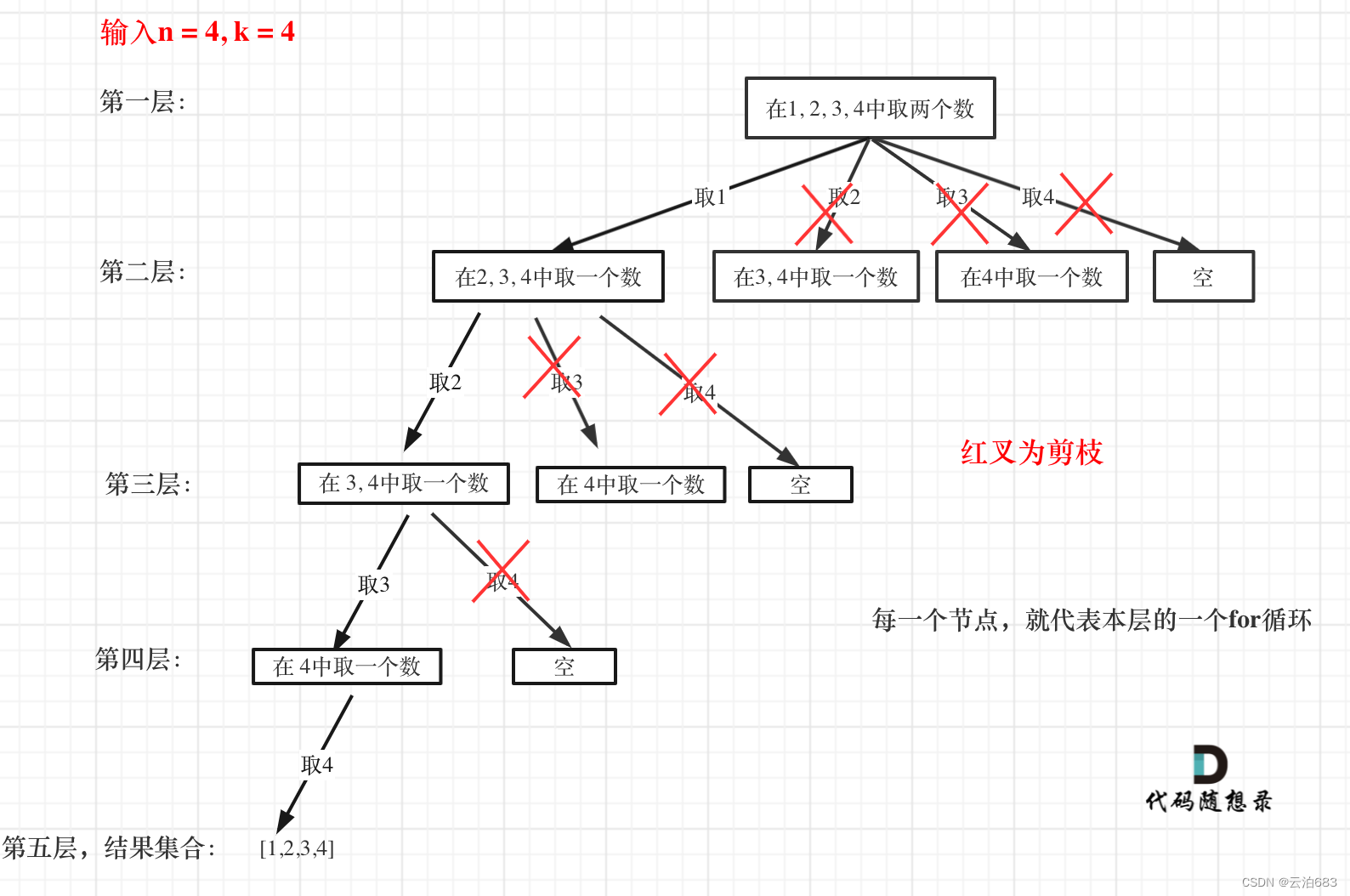
单层搜索，for里面套递归，遍历每一条路径（如下“2.2.思路”下面图片的红色箭头），在递归路径的途中用sum搜集path上每一段的值，用于终止条件。

for (int i = startIndex; i <= 9; i++) {
    sum += i;
    path.push_back(i);
    backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
    sum -= i; // 回溯
    path.pop_back(); // 回溯
}

2.4.总代码：

class Solution {
private:
    vector<vector<int>> result; // 存放结果集
    vector<int> path; // 符合条件的结果
    // targetSum：目标和，也就是题目中的n。
    // k：题目中要求k个数的集合。
    // sum：已经收集的元素的总和，也就是path里元素的总和。
    // startIndex：下一层for循环搜索的起始位置。
    void backtracking(int targetSum, int k, int sum, int startIndex) {
        if (path.size() == k) {
            if (sum == targetSum) result.push_back(path);
            return; // 如果path.size() == k 但sum != targetSum 直接返回
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i; // 处理
            path.push_back(i); // 处理
            backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
            sum -= i; // 回溯
            path.pop_back(); // 回溯
        }
    }

public:
    vector<vector<int>> combinationSum3(int k, int n) {
        result.clear(); // 可以不加
        path.clear();   // 可以不加
        backtracking(n, k, 0, 1);
        return result;
    }
};

3.剪枝优化

3.3.思路：

3.3.1.总和大于n剪枝。

已选元素总和如果已经大于n了，那么往后遍历就没有意义了，直接剪掉。（在终止条件那加上）

 代码如下：

if (sum > targetSum) { // 剪枝操作
    return;
}

3.3.2.已选元素数量+可选元素数量 < 题目需要的元素数量 k 剪枝。

代码如下：

for (int i = startIndex; i <= n - (k - path.size()) + 1; i++) { // 优化的地方

 （忘记怎么来的可以去001.组合看）

4.记录：

不该早上开游戏的，一出现事情很消耗精力，休息时间再回复消息（除非我去问的），不然老是分心。