一、本周周赛总结

• 第一次打CC只能打DIV4.
• P1P2模拟。
• P3 BFS。
• P4 贪心。
• P5 计数讨论。
• P6 二进制贪心。
• P7 质因数分解贪心。
• 
• 

P1 CodeChef Learn Problem Solving

链接: CodeChef Learn Problem Solving

1. 题目描述

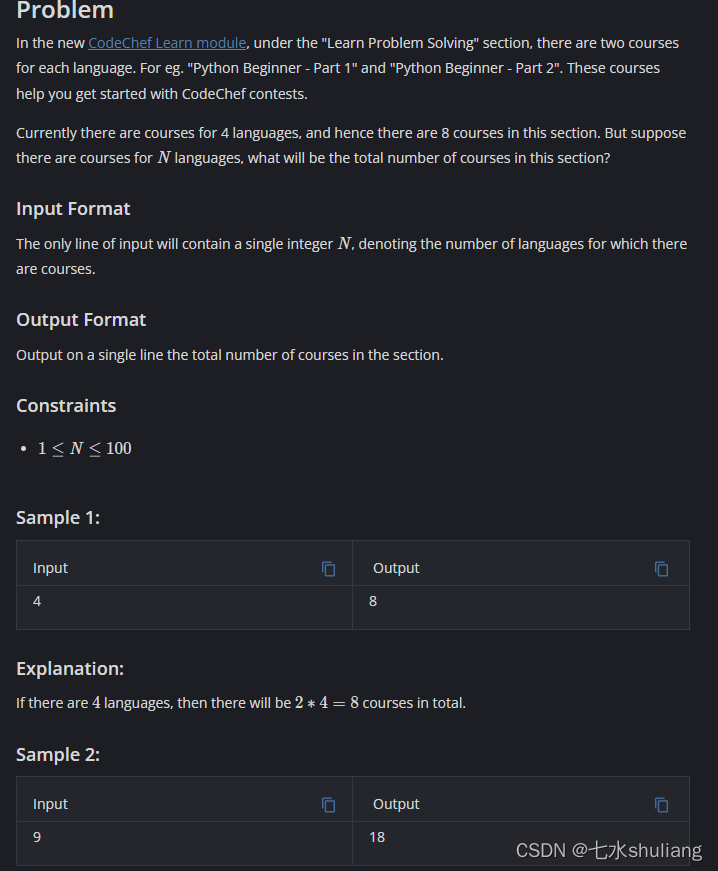
• 输入n种语言，每种语言有两门课，一共几门课？

2. 思路分析

• 模拟。

3. 代码实现

print(int(input())*2)

P2、Cricket Match

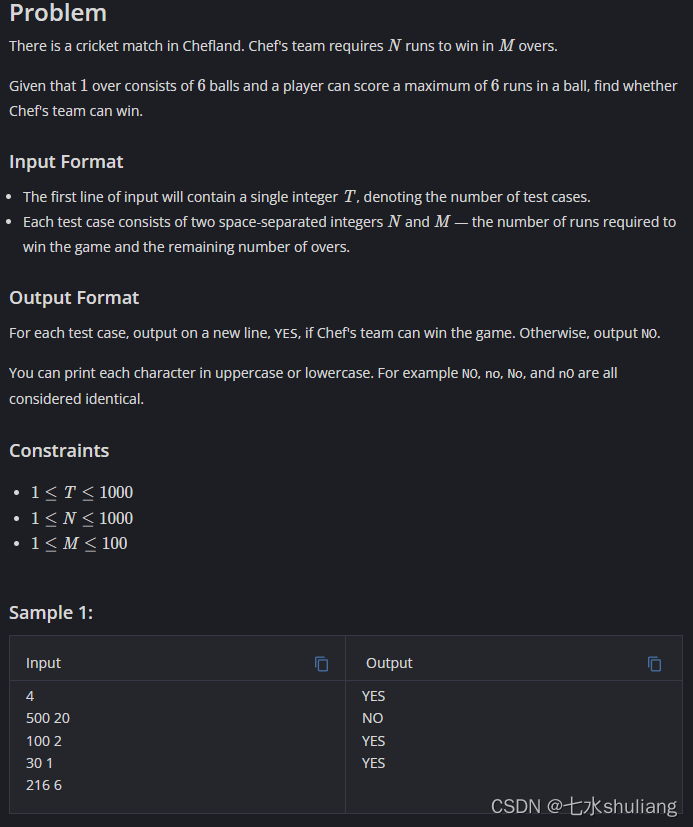
• 板球比赛每轮包括6球，每球能赢6分。
• 需要n分才能赢，还剩m轮，问能不能赢。

2. 思路分析

• 模拟

3. 代码实现

#       ms
def solve():
    n,m = RI()
    if n <= m*6*6:
        print('YES')
    else:
        print('NO')

P3 Chef and Battery

链接: Chef and Battery

1. 题目描述

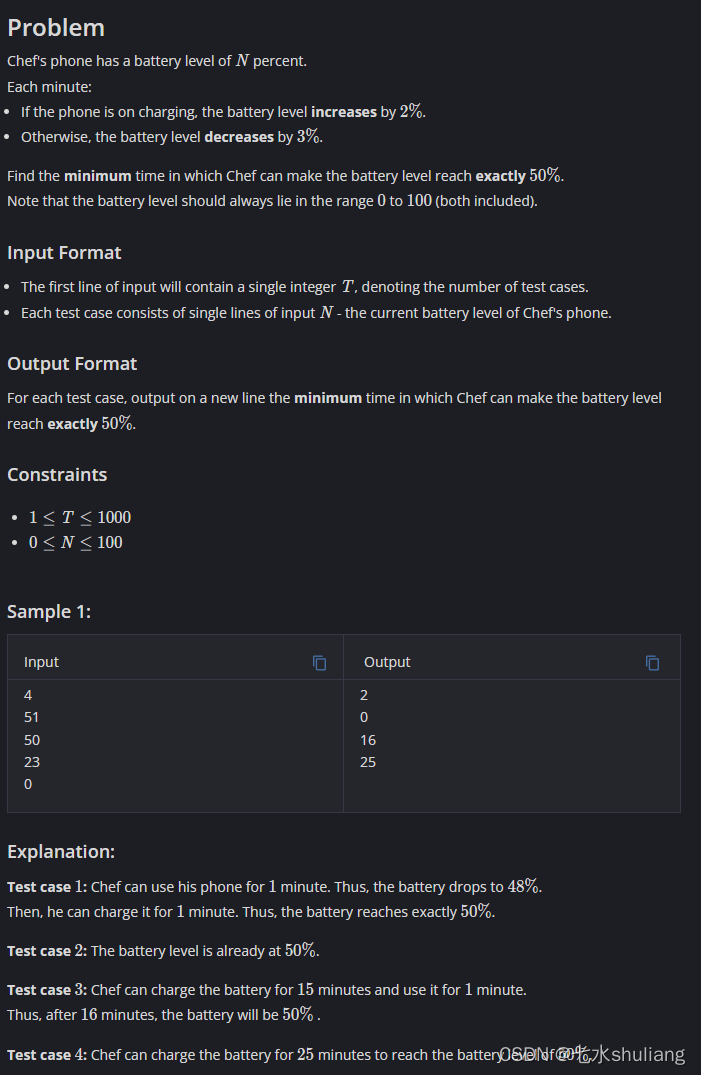
• chef的手机还剩n%电。
• 每分钟手机电量如下变化：
  • 如果手机在充电，会涨2%。
  • 否则，会掉3%.
• 问：Chef最少要用几分钟可以使手机电量到达正好50%。
• 注意手机电量必须在范围[0,100]闭区间。

2. 思路分析

• 这题有点问题，最开始我以为手机在1%电，可以掉一分钟到0%。提交上去WA了。
• 过的代码如下，1%的手机必须充电，不可以掉电。
• 就离谱。

---

• 另外，这题直接while贪心模拟也可以，手机<50则冲>50则掉。

3. 代码实现

# Problem: Chef and Battery
# Contest: CodeChef - START86D
# URL: https://www.codechef.com/START86D/problems/FIFTYPE
# Memory Limit: 256 MB
# Time Limit: 1000 ms

import sys
from collections import *

RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')


#       ms
def solve():
    n, = RI()
    if n == 50:
        return print(0)
    t = 0
    vis = {n}
    q = deque([n])
    while q:
        t += 1
        for _ in range(len(q)):
            u = q.popleft()
            for v in u - 3, u + 2:
                if v == 50:
                    return print(t)
                if v < 0 or v > 100:
                    continue
                if v not in vis:
                    vis.add(v)
                    q.append(v)


if __name__ == '__main__':
    t, = RI()
    for _ in range(t):
        solve()

P4 Maximise Score

链接: Maximise Score

1. 题目描述

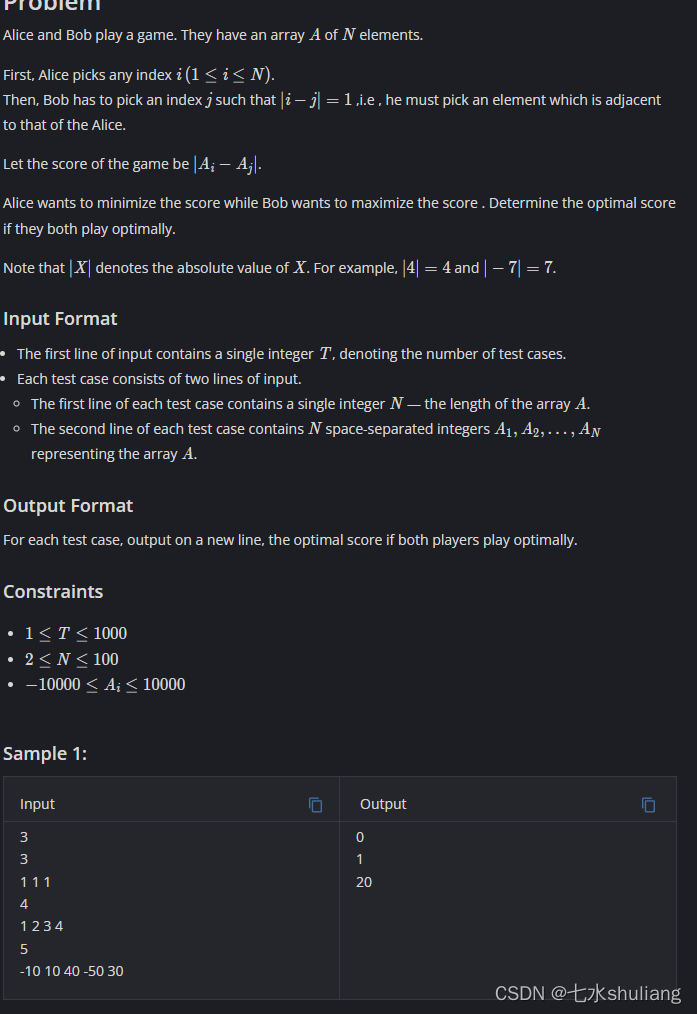
• AB玩游戏，输入n和长为n的数组a。
• A选一个下标i，B选i相邻的下标，最后分数为abs(a[i]-a[j])。
• A目的是让分数小，B目的是让分数大。

2. 思路分析

• 看起来是博弈，其实是2次贪心。
• 首先A一定可以选0或n-1，这样B没有操作空间，答案必是前两个数或后两个数的差。
  • 即可以初始化为ans = min(abs(a[0]-a[1]),abs(a[-1]-a[-2]))
• 然后枚举A可以选择的剩下位置i in range(1,n-1)，B一定可以选择两边的差中最大的那个。
  • 那么A只要尝试从最大值里选最小。

3. 代码实现

def solve():
    n, = RI()
    a = RILST()
    ans = min(abs(a[0]-a[1]),abs(a[-1]-a[-2]))
    for i in range(1,n-1):
        x = max(abs(a[i]-a[i-1]),abs(a[i]-a[i+1]))
        ans = min(ans,x)
    print(ans )

P5 String Game

链接: String Game

1. 题目描述

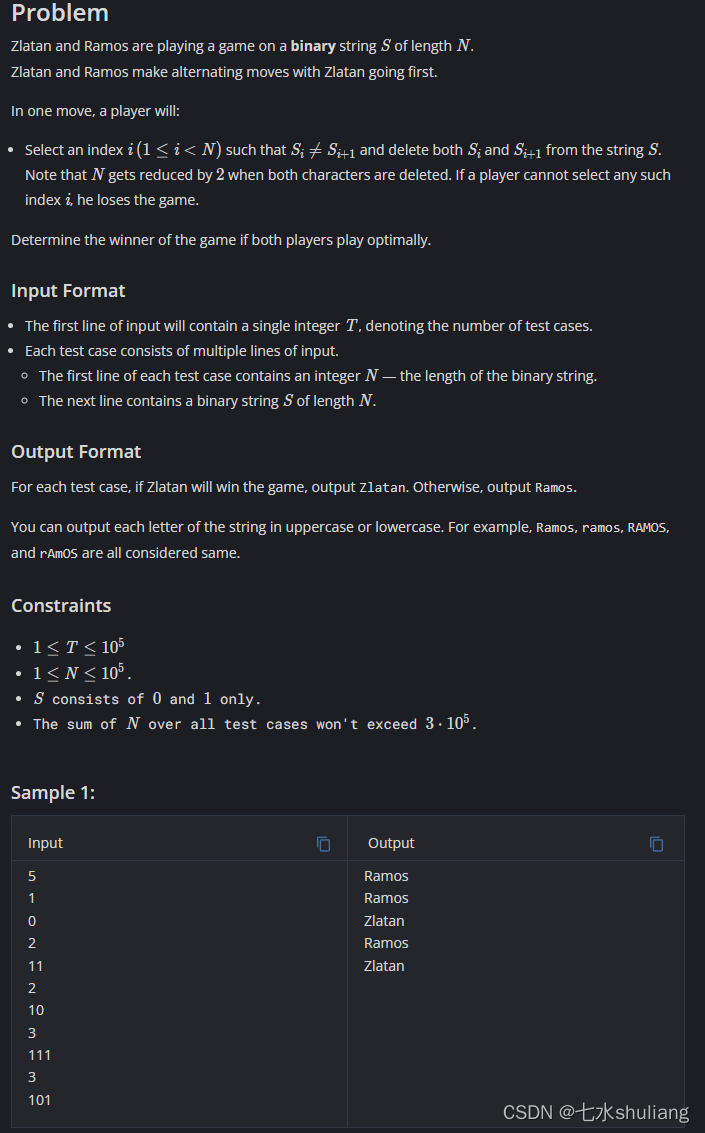
• 输入一个二进制串S。
• AB在S上玩游戏。每轮操作：
  • 当前玩家可以选一个s[i]!=s[i+1]的位置，删除这两个字符。
• 无法操作的玩家输。

2. 思路分析

• 看起来又是博弈。
• 统计01出现次数cnt=Counter(s)。
• 显然若一开始就没有01相邻出现，A肯定输。
• 若有01出现，每次删除会同时删除01各一次，且剩下的串若有01，必然可以继续操作。
• 那么一共可以删除的次数就是01次数里的最小值。
• 这个次数是奇数则A赢；否则B赢。

3. 代码实现

def solve():
    n, = RI()
    s, = RS()
    cnt = Counter(s)
    if len(cnt) != 2:
        return print('Ramos')
    x = min(cnt.values())
    if x&1:
        print('Zlatan')
    else:
        print('Ramos')

P6 Largest Y

链接: Largest Y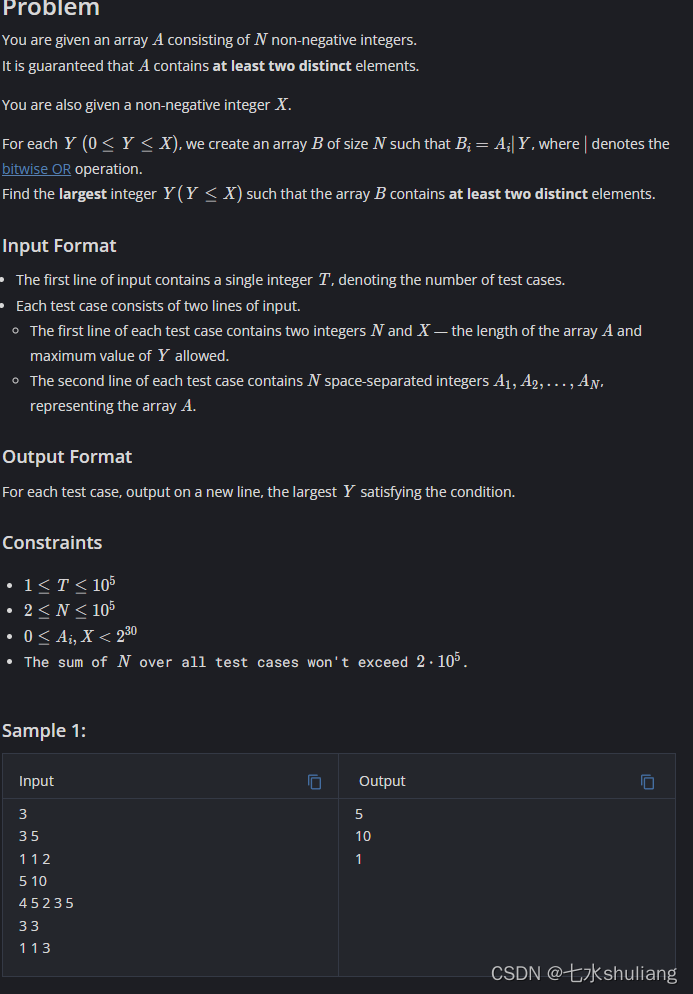

• 输入n，x和长为n的数组a。题目保证a中至少有2个不同的元素。(2<=n<=1e5);(x,a[i]<=2^30,)
• 你可以选择一个数y(y<=x)，构造数组b，其中b[i]=a[i]|y。即a中每个数或上y。要求b也至少有2个不同元素。
• 求最大的y。

2. 思路分析

• 二进制贪心，幸好做出来了。
• 考虑b中数据，所有b[i]中，只要有一位存在不同值，既有0也有1，则b就满足要求。
• 从低到高枚举每一位，check a中当前位是否存在不同值，若存在，只需要y的当前位是0，则b中对应的这个位不会变，即满足要求。若第i位满足：
  • 查看x中第i位是否是0，若是0，x本身就可以作为答案，因为要求y<=x,不可超过x。
  • 若x中第i位是1，尝试把这位变成0，b就满足了；为了使答案尽可能大，使低于i的位全变1，高于i的位不变。

---

• 这里有个问题，需要计算a中第i位是否存在不同值，怎么写更方便。
  • 我采用的是每一位创建set的写法，把这位加入set，看set长度是不是2。
  • 注意，到达2时，就可以进行答案计算了；并且由于是从低到高枚举，其实它已经是变1操作的最大值了。
  • 但是不可以return，只能break掉枚举当前位的操作。这是因为：后边还有可能有的位x本身就是0，这才是最大的。
• 因此其实可以把两种情况分开，都只需要判断一次就跳出。
• 所以可以采用sovle1的写法：
  • 令 c = reduce(ior, a) d = reduce(iand, a) e=c-d。
  • c是a位或起来，所有有1的位置是1；d是a位于起来，所有只有1的位置是1。
  • 那么e就是a中同时有1和0的位置。其他位置都是0。
  • x&e若==e，代表e中所有1的位置在x里也是1；否则必有一个e中的1，在x里是0，位于才会修改e。这时就可以直接用x。
  • 否则找最低的位直接计算答案即可，这里也可以优化。
  • 由于我们目的是把x位上的这个1变成0，后边的全变1。那么可以把后边先全变0，然后直接x-=1。
  • 后边全变0的操作可以直接减去对这个2次幂取模的值。具体见代码。

3. 代码实现

def solve():
    n, x = RI()
    a = RILST()
    c = reduce(ior, a)
    d = reduce(iand, a)
    e = c - d
    if (x & e) != e:
        return print(x)
    for i in range(31):
        if e >> i & 1:
            x -= x % (1 << i)
            return print(x - 1)


def solve1():
    n, x = RI()
    a = RILST()
    ans = 0
    for i in range(31):
        p = set()
        for v in a:
            z = (v >> i) & 1
            p.add(z)
            if len(p) == 2:
                if (x >> i) & 1:
                    ans = max(ans, (x ^ (1 << i)) | ((1 << i) - 1))
                    break
                else:
                    return print(x)
    print(ans)

P7 Minimum Operation

链接: Minimum Operation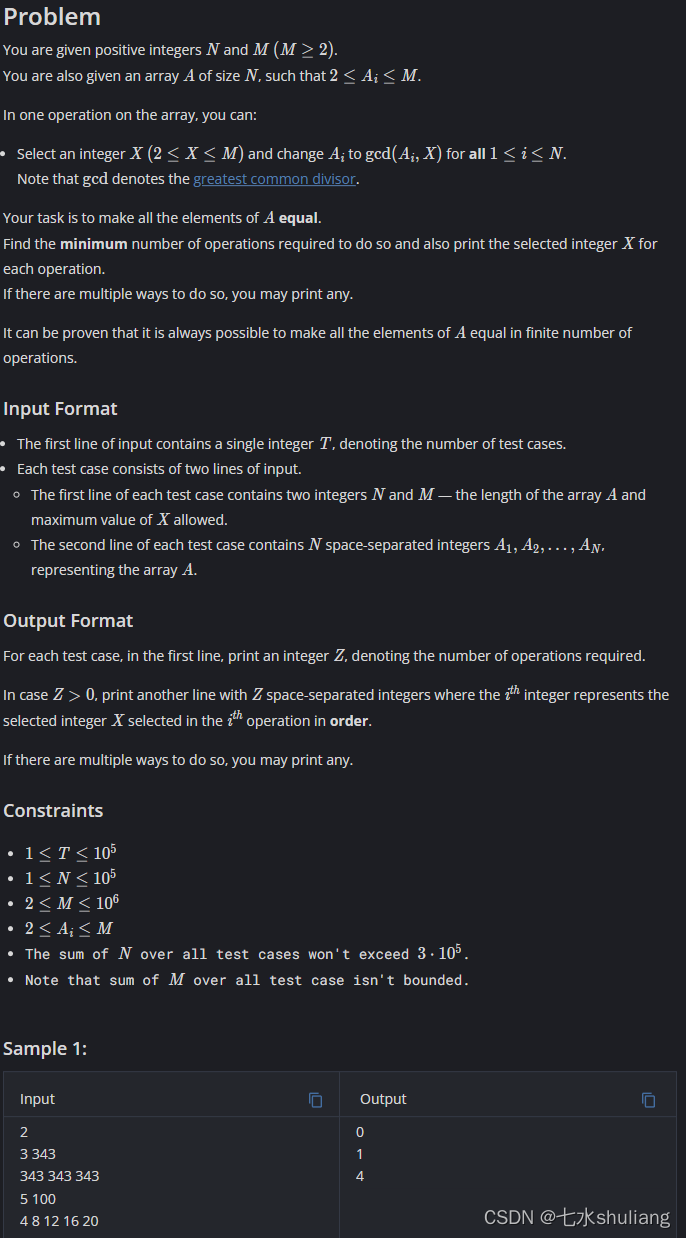

• 输入n,m和长为n的数组a,其中2<=a[i]<=m。
• 每步操作你可以:
  • 选择一个x(2<=x<=m) 把所有a[i]替换成gcd(x,a[i])。
• 问最少多少步，可以让a中所有数字相同。
• 输出步数和每一步的选择。

2. 思路分析

• 这一看，直接选x=1，一步就完事了！仔细一看x必须>=2。
• 那么我可以直接选2，a中只剩下2和1；再选个3，直接就搞定了。
• 先计算a中所有数字的gcd记为g，若g>=2,那么可以选g，一步就可以把a变成全g。
• 然后从小到大枚举<=m的所有质数v，若v和所有a[i]互质，则一步就可以把a变成全1。
  • 如何计算互质呢，只需要所有a[i]中没有这个质因子，那么分解每个a[i]用set记录即可。
  • 你可能认为这里枚举复杂度是m(1e6中有78498个素数)，一共T组数据会不会超时。这是不会的。
    • 因为s是很稀疏的。若要使复杂度到达m，需要s稠密，即a中存在所有这七万多个素数。那么a的长度很长，T就会很小。

3. 代码实现

def solve():
    n, m = RI()
    a = set(RILST())
    if len(a) == 1:
        return print(0)
    g = reduce(gcd, a)
    if g >= 2:
        print(1)
        return print(g)

    s = set()
    for x in a:
        i = 2
        while i * i <= x:
            while x % i == 0:
                s.add(i)
                x //= i
            i += 1
        if x > 1: s.add(x)

    for v in ps:
        if v > m: break
        if v not in s:
            print(1)
            return print(v)

    print(2)
    print(2)
    print(3)

六、参考链接

• 无