127. 单词接龙 Word Ladder 🌟🌟🌟

128. 最长连续序列 Longest Consecutive Sequence 🌟🌟

129. 求根节点到叶节点数字之和 Sum Root-to-leaf Numbers 🌟🌟

🌟 每日一练刷题专栏 🌟

Golang每日一练专栏

Python每日一练专栏

C/C++每日一练专栏

Java每日一练专栏

127. 单词接龙 Word Ladder

字典 wordList 中从单词 beginWord 和 endWord 的 转换序列 是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk：

每一对相邻的单词只差一个字母。
对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。
sk == endWord

给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回从 beginWord 到 endWord 的 最短转换序列 中的 单词数目 。如果不存在这样的转换序列，返回 0 。

示例 1：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

示例 2：

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log"]
输出：0
解释：endWord "cog" 不在字典中，所以无法进行转换。

提示：

1 <= beginWord.length <= 10
endWord.length == beginWord.length
1 <= wordList.length <= 5000
wordList[i].length == beginWord.length
beginWord、endWord 和 wordList[i] 由小写英文字母组成
beginWord != endWord
wordList 中的所有字符串 互不相同

相关：

126. 单词接龙 II Word Ladder II 🌟🌟🌟

代码1： BFS

package main

import (
	"fmt"
)

func ladderLength(beginWord string, endWord string, wordList []string) int {
	wordSet := make(map[string]bool) // 存储单词表中的单词，用于删除操作
	for _, word := range wordList {
		wordSet[word] = true
	}
	if !wordSet[endWord] {
		return 0 // 单词表中不包含结束单词，无法进行转换
	}
	visited := make(map[string]bool) // 存储已访问过的单词
	visited[beginWord] = true
	queue := []string{beginWord} // 存储待遍历的节点
	level := 1                   // 存储当前节点所处的层数，即转换序列的长度
	for len(queue) > 0 {
		size := len(queue)
		for i := 0; i < size; i++ {
			currWord := queue[0]
			queue = queue[1:]
			if currWord == endWord {
				return level // 找到了最短路径，返回转换序列的长度
			}
			for _, nextWord := range getNextWords(currWord, wordSet) {
				if !visited[nextWord] {
					visited[nextWord] = true
					queue = append(queue, nextWord)
				}
			}
		}
		level++ // 当前层的所有节点遍历完后，转换序列长度加 1
	}
	return 0 // 无法进行转换
}

// 获取与当前单词相差一个字母的单词列表
func getNextWords(word string, wordSet map[string]bool) []string {
	words := make([]string, 0)
	for i := 0; i < len(word); i++ {
		for j := 'a'; j <= 'z'; j++ {
			if byte(j) == word[i] {
				continue // 将当前字母跳过，避免重复
			}
			newWord := word[:i] + string(j) + word[i+1:]
			if wordSet[newWord] {
				words = append(words, newWord)
				delete(wordSet, newWord) // 将该单词从单词表中删除，避免重复遍历
			}
		}
	}
	return words
}

func main() {
	beginWord, endWord := "hit", "cog"
	wordList := []string{"hot", "dot", "dog", "lot", "log", "cog"}
	fmt.Println(ladderLength(beginWord, endWord, wordList))
	wordList = []string{"hot", "dot", "dog", "lot", "log"}
	fmt.Println(ladderLength(beginWord, endWord, wordList))
}

代码2： 双向 BFS

package main

import (
	"fmt"
)

func ladderLength(beginWord string, endWord string, wordList []string) int {
	wordSet := make(map[string]bool) // 存储单词表中的单词，用于删除操作
	for _, word := range wordList {
		wordSet[word] = true
	}
	if !wordSet[endWord] {
		return 0 // 单词表中不包含结束单词，无法进行转换
	}
	visited := make(map[string]bool) // 存储已访问过的单词
	visited[beginWord] = true
	visited[endWord] = true
	queue1 := []string{beginWord} // 存储起点开始的待遍历节点
	queue2 := []string{endWord}   // 存储终点开始的待遍历节点
	level := 1                    // 存储当前节点所处的层数，即转换序列的长度
	for len(queue1) > 0 && len(queue2) > 0 {
		if len(queue1) > len(queue2) {
			queue1, queue2 = queue2, queue1 // 交换两个队列，保证 queue1 中的节点数目少于等于 queue2 中的节点数目
		}
		size := len(queue1)
		for i := 0; i < size; i++ {
			currWord := queue1[0]
			queue1 = queue1[1:]
			for _, nextWord := range getNextWords(currWord, wordSet) {
				if visited[nextWord] { // 如果从另一个方向已经访问过该节点，说明两个搜索相遇了，找到了最短路径
					return level + 1
				}
				if !visited[nextWord] {
					visited[nextWord] = true
					queue1 = append(queue1, nextWord)
				}
			}
		}
		level++ // 当前层的所有节点遍历完后，转换序列长度加 1
	}
	return 0 // 无法进行转换
}

// 获取与当前单词相差一个字母的单词列表
func getNextWords(word string, wordSet map[string]bool) []string {
	words := make([]string, 0)
	for i := 0; i < len(word); i++ {
		for j := 'a'; j <= 'z'; j++ {
			if byte(j) == word[i] {
				continue // 将当前字母跳过，避免重复
			}
			newWord := word[:i] + string(j) + word[i+1:]
			if wordSet[newWord] {
				words = append(words, newWord)
				delete(wordSet, newWord) // 将该单词从单词表中删除，避免重复遍历
			}
		}
	}
	return words
}

func main() {
	beginWord, endWord := "hit", "cog"
	wordList := []string{"hot", "dot", "dog", "lot", "log", "cog"}
	fmt.Println(ladderLength(beginWord, endWord, wordList))
	wordList = []string{"hot", "dot", "dog", "lot", "log"}
	fmt.Println(ladderLength(beginWord, endWord, wordList))
}

输出：

5
0

代码3： 用126题的结果遍历出最大长度

package main

import (
	"fmt"
)

func ladderLength(beginWord string, endWord string, wordList []string) int {
	res := 0
	for _, arr := range findLadders(beginWord, endWord, wordList) {
		size := len(arr)
		if res < size {
			res = len(arr)
		}
	}
	return res
}

func findLadders(beginWord string, endWord string, wordList []string) [][]string {
	result, wordMap := make([][]string, 0), make(map[string]bool)
	for _, w := range wordList {
		wordMap[w] = true
	}
	if !wordMap[endWord] {
		return result
	}
	queue := make([][]string, 0)
	queue = append(queue, []string{beginWord})
	queueLen := 1
	levelMap := make(map[string]bool)
	for len(queue) > 0 {
		path := queue[0]
		queue = queue[1:]
		lastWord := path[len(path)-1]
		for i := 0; i < len(lastWord); i++ {
			for c := 'a'; c <= 'z'; c++ {
				nextWord := lastWord[:i] + string(c) + lastWord[i+1:]
				if nextWord == endWord {
					path = append(path, endWord)
					result = append(result, path)
					continue
				}
				if wordMap[nextWord] {
					levelMap[nextWord] = true
					newPath := make([]string, len(path))
					copy(newPath, path)
					newPath = append(newPath, nextWord)
					queue = append(queue, newPath)
				}
			}
		}
		queueLen--
		if queueLen == 0 {
			if len(result) > 0 {
				break
			}
			for k := range levelMap {
				delete(wordMap, k)
			}
			levelMap = make(map[string]bool)
			queueLen = len(queue)
		}
	}
	return result
}

func main() {
	beginWord, endWord := "hit", "cog"
	wordList := []string{"hot", "dot", "dog", "lot", "log", "cog"}
	fmt.Println(ladderLength(beginWord, endWord, wordList))
	wordList = []string{"hot", "dot", "dog", "lot", "log"}
	fmt.Println(ladderLength(beginWord, endWord, wordList))
}

128. 最长连续序列 Longest Consecutive Sequence

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

示例 2：

输入：nums = [0,3,7,2,5,8,4,6,0,1]
输出：9

提示：

0 <= nums.length <= 10^5
-10^9 <= nums[i] <= 10^9

代码1：

package main

import (
	"fmt"
)

func longestConsecutive(nums []int) int {
	numSet := map[int]bool{}
	for _, num := range nums {
		numSet[num] = true
	}
	longestStreak := 0
	for num := range numSet {
		if !numSet[num-1] {
			currentNum := num
			currentStreak := 1
			for numSet[currentNum+1] {
				currentNum++
				currentStreak++
			}
			if currentStreak > longestStreak {
				longestStreak = currentStreak
			}
		}
	}
	return longestStreak
}

func main() {
	nums := []int{100, 4, 200, 1, 3, 2}
	fmt.Println(longestConsecutive(nums))
	nums = []int{0, 3, 7, 2, 5, 8, 4, 6, 0, 1}
	fmt.Println(longestConsecutive(nums))
}

输出：

4
9

代码2：

package main

import (
	"fmt"
	"sort"
)

func longestConsecutive(nums []int) int {
	n := len(nums)
	if n == 0 {
		return 0
	}
	sort.Ints(nums)
	maxLength, currentLength := 1, 1
	for i := 1; i < n; i++ {
		if nums[i] != nums[i-1] {
			if nums[i] == nums[i-1]+1 {
				currentLength++
			} else {
				if maxLength < currentLength {
					maxLength = currentLength
				}
				currentLength = 1
			}
		}
	}
	if maxLength < currentLength {
		maxLength = currentLength
	}
	return maxLength
}

func main() {
	nums := []int{100, 4, 200, 1, 3, 2}
	fmt.Println(longestConsecutive(nums))
	nums = []int{0, 3, 7, 2, 5, 8, 4, 6, 0, 1}
	fmt.Println(longestConsecutive(nums))
}

129. 求根节点到叶节点数字之和 Sum Root-to-leaf Numbers

给你一个二叉树的根节点 root ，树中每个节点都存放有一个 0 到 9 之间的数字。

每条从根节点到叶节点的路径都代表一个数字：

例如，从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。

计算从根节点到叶节点生成的 所有数字之和 。

叶节点 是指没有子节点的节点。

示例 1：

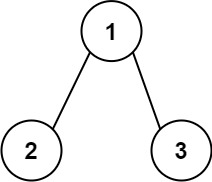
输入：root = [1,2,3]
输出：25
解释：
从根到叶子节点路径 1->2 代表数字 12
从根到叶子节点路径 1->3 代表数字 13
因此，数字总和 = 12 + 13 = 25

示例 2：

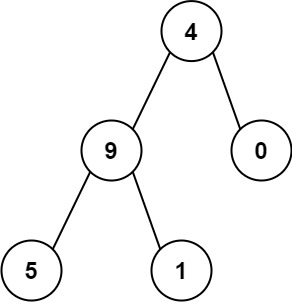
输入：root = [4,9,0,5,1]
输出：1026
解释：
从根到叶子节点路径 4->9->5 代表数字 495
从根到叶子节点路径 4->9->1 代表数字 491
从根到叶子节点路径 4->0 代表数字 40
因此，数字总和 = 495 + 491 + 40 = 1026

提示：

树中节点的数目在范围 [1, 1000] 内
0 <= Node.val <= 9
树的深度不超过 10

代码1： DFS

package main

import (
	"fmt"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func sumNumbers(root *TreeNode) int {
	if root == nil {
		return 0
	}
	stack := []*TreeNode{root}
	res := 0
	for len(stack) > 0 {
		node := stack[len(stack)-1]
		stack = stack[:len(stack)-1]
		if node.Left == nil && node.Right == nil {
			res += node.Val
			continue
		}
		if node.Right != nil {
			node.Right.Val += node.Val * 10
			stack = append(stack, node.Right)
		}
		if node.Left != nil {
			node.Left.Val += node.Val * 10
			stack = append(stack, node.Left)
		}
	}
	return res
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func main() {
	nums := []int{1, 2, 3}
	root := buildTree(nums)
	fmt.Println(sumNumbers(root))
	nums = []int{4, 9, 0, 5, 1}
	root = buildTree(nums)
	fmt.Println(sumNumbers(root))
}

输出：

25
1026

代码2： 递归

package main

import (
	"fmt"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func sumNumbers(root *TreeNode) int {
	return dfs(root, 0)
}

func dfs(root *TreeNode, prevSum int) int {
	if root == nil {
		return 0
	}
	sum := prevSum*10 + root.Val
	if root.Left == nil && root.Right == nil {
		return sum
	}
	return dfs(root.Left, sum) + dfs(root.Right, sum)
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func main() {
	nums := []int{1, 2, 3}
	root := buildTree(nums)
	fmt.Println(sumNumbers(root))
	nums = []int{4, 9, 0, 5, 1}
	root = buildTree(nums)
	fmt.Println(sumNumbers(root))
}

代码3： binaryTreePaths()结果求和，相关题目：

112. 路径总和 Path Sum 🌟

113. 路径总和 II Path Sum II 🌟🌟

package main

import (
	"fmt"
)

const null = -1 << 31

type TreeNode struct {
	Val   int
	Left  *TreeNode
	Right *TreeNode
}

func sumNumbers(root *TreeNode) int {
	toNum := func(arr []int) int {
		num, base := 0, 1
		for i := len(arr) - 1; i >= 0; i-- {
			num += arr[i] * base
			base *= 10
		}
		return num
	}
	res := 0
	for _, path := range binaryTreePaths(root) {
		res += toNum(path)
	}
	return res
}

func binaryTreePaths(root *TreeNode) [][]int {
	res := [][]int{}
	if root == nil {
		return res
	}
	if root.Left == nil && root.Right == nil {
		return [][]int{{root.Val}}
	}
	leftPaths := binaryTreePaths(root.Left)
	rightPaths := binaryTreePaths(root.Right)

	paths := make([][]int, 0)
	for _, path := range leftPaths {
		paths = append(paths, append([]int{root.Val}, path...))
	}
	for _, path := range rightPaths {
		paths = append(paths, append([]int{root.Val}, path...))
	}
	return paths
}

func buildTree(nums []int) *TreeNode {
	if len(nums) == 0 {
		return nil
	}
	root := &TreeNode{Val: nums[0]}
	Queue := []*TreeNode{root}
	idx := 1
	for idx < len(nums) {
		node := Queue[0]
		Queue = Queue[1:]
		if nums[idx] != null {
			node.Left = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Left)
		}
		idx++
		if idx < len(nums) && nums[idx] != null {
			node.Right = &TreeNode{Val: nums[idx]}
			Queue = append(Queue, node.Right)
		}
		idx++
	}
	return root
}

func main() {
	nums := []int{1, 2, 3}
	root := buildTree(nums)
	fmt.Println(sumNumbers(root))
	nums = []int{4, 9, 0, 5, 1}
	root = buildTree(nums)
	fmt.Println(sumNumbers(root))
}