4.6.1 最小二乘问题的提法

学习目标：

要学习曲线拟合的最小二乘法，我会按照以下步骤进行：

理解最小二乘法的基本思想和原理，即在已知数据的情况下，通过拟合一条曲线，使得曲线与数据之间的误差最小化。
学习线性回归模型的基本知识，了解如何使用最小二乘法来拟合线性模型，并掌握其相关数学知识。
深入了解非线性回归模型的拟合方法，学习如何使用最小二乘法来拟合非线性模型，并了解相应的数学知识和算法实现方法。
掌握使用Python等编程语言实现最小二乘法的技巧，了解如何使用现有的数学库和工具来实现曲线拟合。
学习如何评估曲线拟合的好坏，了解常用的拟合评估指标，如均方误差、R2值等，并掌握如何使用这些指标来评估模型的性能。
通过实际应用案例来加深对曲线拟合的理解和掌握，了解如何根据具体的问题选择适合的拟合模型和算法。
不断实践和思考，积累经验，不断提高自己的技能和能力，成为一名优秀的曲线拟合专家。

4.6.1 最小二乘问题的提法

最小二乘问题是指，给定一个数据集和一个数学模型，通过最小化数据集中预测值和真实值之间的差异的平方和，来确定模型的未知参数的值。这个问题可以表示为以下形式：

其中，\mathbf{y}是一个n维向量，表示数据集中的真实值；\mathbf{X}是一个n\times p的矩阵，表示数学模型的输入；\boldsymbol{\beta}是一个p维向量，表示数学模型的未知参数；||\cdot||_2$表示$L_2范数，即向量的欧几里得距离。

最小二乘问题的目标是找到一个最优的\boldsymbol{\beta}，使得数据集中预测值和真实值之间的差异的平方和最小。这个问题可以通过求解一个线性方程组来得到最优解，具体来说，可以使用矩阵求逆或QR分解等方法来求解。

为什么有最小二乘法

最小二乘问题是为了解决数据集中的真实值和数学模型的预测值之间的差异而提出的。在很多实际问题中，我们需要建立数学模型来对数据进行分析和预测。但是，由于多种原因，这些模型往往不能完美地拟合数据集中的真实值，存在一定的误差。

为了尽可能减小误差，我们需要找到一组最优的数学模型参数，使得数学模型的预测值和真实值之间的差异最小。这就是最小二乘问题需要解决的。最小二乘问题不仅可以用于曲线拟合，还可以用于信号处理、统计回归、数据压缩等领域，是非常重要的数学工具。

6.2 最小二乘解的求法

在最小二乘问题中，我们需要找到一组最优的模型参数来使得拟合函数和数据之间的误差最小。一般来说，最小二乘问题有多种求解方法，以下是其中几种常见的方法：

矩阵求解法：将样本数据中的自变量和因变量组成矩阵形式，建立方程组，用线性代数的方法求解方程组的解即可得到最优参数值。
梯度下降法：通过迭代优化的方式来逐步调整模型参数，直到找到最优参数值。该方法需要选择合适的学习率和迭代次数，能够应对非线性和高维的最小二乘问题。
QR分解法：将矩阵进行QR分解，然后用回代法求解出最优参数值。该方法比较适用于维数较高的问题。

无论使用哪种方法，都需要先建立拟合模型，并将原始数据转化为矩阵形式，然后根据不同的方法来计算模型的最优参数。值得注意的是，在使用最小二乘法进行数据拟合时，我们需要注意过拟合和欠拟合的问题，以免出现模型预测效果不佳的情况。

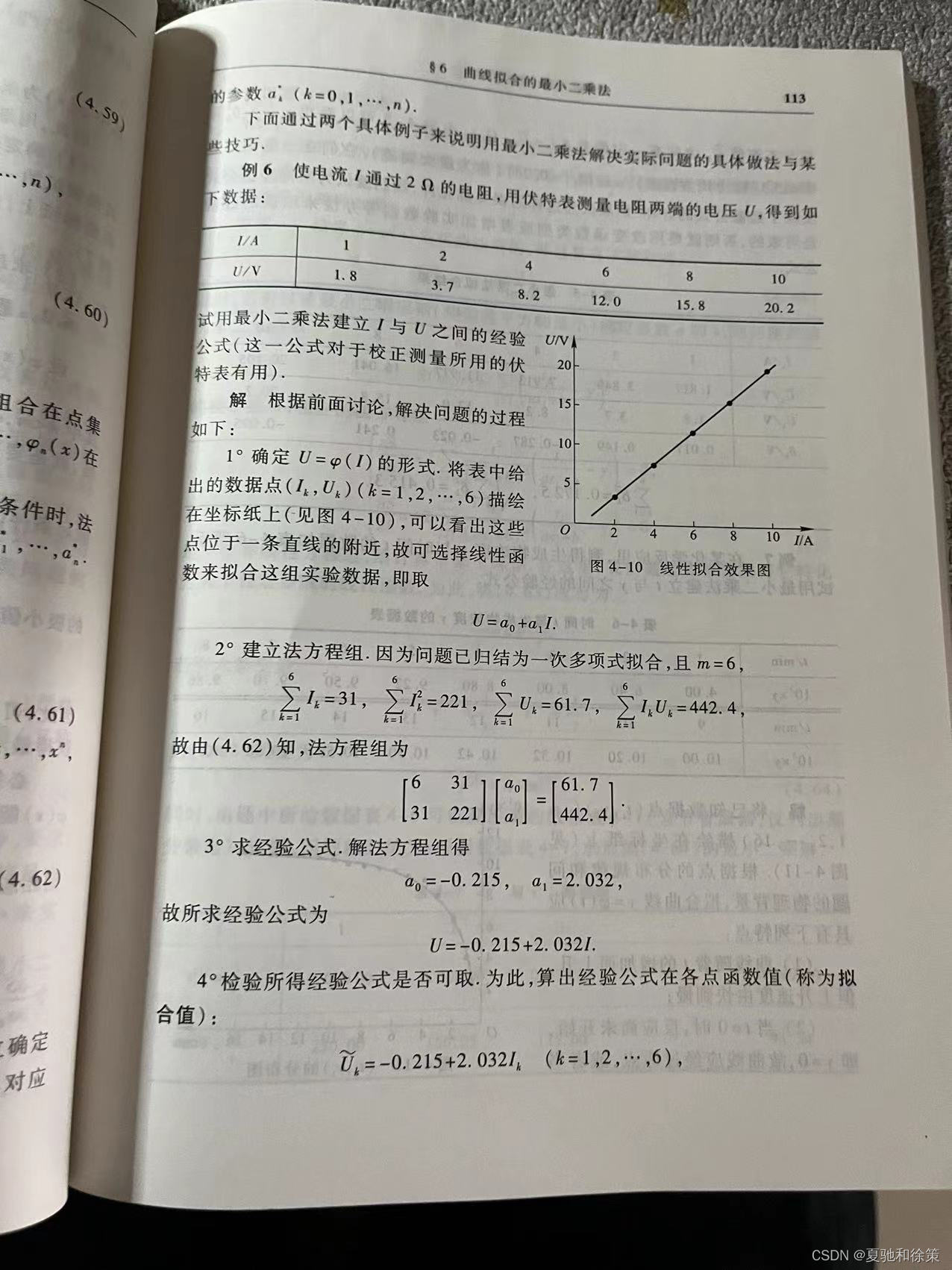
定义11 哈尔条件

哈尔(Haar)条件是指在最小二乘问题中，如果列向量组A的列向量互相正交且归一化，即 $A^T A=I$，那么最小二乘解的求法可以大大简化。此时，最小二乘问题的解可以直接写成：

其中，A是 m\times n的矩阵，b 是 m维向量，x是 n维向量，I是 n维单位矩阵。

哈尔条件的好处是能够使得最小二乘问题的求解变得简单、直观，同时也能够避免由于矩阵 $A$ 列向量的线性相关性或接近线性相关性所导致的求解困难或误差增大的问题。但是，实际应用中能够满足哈尔条件的情况比较少，通常需要通过正交化或者QR分解等方法来满足该条件。

4.6.3 加权技巧的应用

加权技巧在曲线拟合和最小二乘问题中有着广泛的应用。其基本思想是，在最小二乘问题中，通过引入权重矩阵 W，将不同的测量数据给予不同的权重，从而使得拟合结果更加符合实际情况。

在曲线拟合中，加权技巧可以用于控制不同数据点对拟合曲线的贡献，例如在处理异常值时，可以将异常值的权重设置得较小，从而降低其对拟合曲线的影响。

在最小二乘问题中，加权技巧可以用于处理不同的误差方差，例如在某些应用中，不同的数据点可能存在不同的测量误差，因此可以根据其误差方差对不同的数据点进行加权处理，从而更好地反映实际情况。

加权技巧的具体实现方式包括改变误差平方和的权重、引入加权矩阵等。需要注意的是，加权技巧的应用需要根据具体问题进行权衡和调整，否则可能会导致拟合结果的偏差和误差增大。

迭代因子最小二乘法：

迭代权最小二乘法是一种解决最小二乘问题的迭代算法。与最小二乘法相似，它也是通过寻找最小化误差的方法来拟合数据。不过在迭代权最小二乘法中，每个数据点都有一个权重，这些权重可以通过多次迭代来逐步优化。其基本思想是，对于每次迭代，我们先根据当前权重求出一个最小二乘解，然后再根据这个解计算新的权重，并用新的权重进行下一轮迭代。

具体来说，假设我们有m个数据点(x1, y1), (x2, y2), ..., (xm, ym)，并且我们要拟合一个n次多项式y = a0 + a1x + a2x^2 + ... + anx^n，其中a0, a1, ..., an是待求的系数。设p(x)表示这个多项式，我们的目标是找到一个最小二乘解，使得误差E = Σwi(pi - yi)^2最小。其中pi = p(xi)是多项式在第i个数据点处的值，wi是第i个数据点的权重。如果我们知道每个数据点的权重，我们可以用最小二乘公式求解系数a0, a1, ..., an。

但是，如果我们不知道每个数据点的真实权重，我们可以先随意选择一组初始权重w1, w2, ..., wm，然后通过以下迭代公式来逐步更新权重：

wi = 1 / (pi - yi)^2

其中pi = p(xi)是当前多项式在第i个数据点处的值。注意这个迭代公式只有在pi不等于yi时才有意义，否则分母为0。在每次迭代中，我们先用当前权重求解最小二乘解，然后再用新的解计算新的权重。我们可以一直迭代下去，直到权重收敛为止。

迭代权最小二乘法的优点是可以通过逐步调整权重来适应数据的分布情况，从而得到更好的拟合结果。缺点是需要进行多次迭代，每次迭代都需要重新计算多项式的系数，计算量较大。此外，初始权重的选择对最终结果也有影响，需要一定的经验或试错来确定。