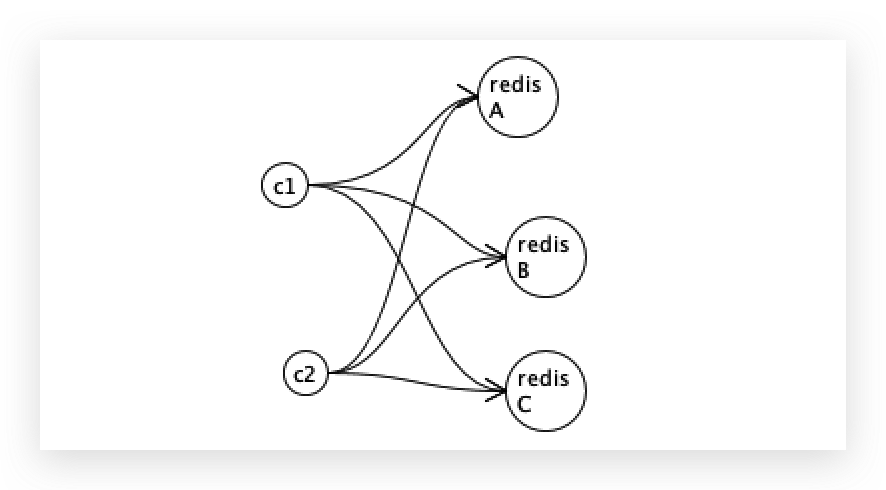
有序序列查找可以用二分查找,但其插入删除需要移动数据,较为复杂;若不想多的移动,可以弄成无序序列,但这样就不能用二分查找。
为了不影响数据顺序,可以使用二叉排序树,
概念:
二叉排序树又叫二叉搜索树,是一棵空树或是具有以下性质的二叉树:
每个结点都有一个作为搜索依据的关键码key,所有结点的关键码 互不相同;
左子树上所有结点的关键码都小于根结点的关键码;
右子树上所有结点的关键码都大于根结点的关键码、
左右子树也是二叉搜索树;
中序遍历这棵树,是从小到大排好序的;
最左边的孩子一定是最小的结点,最右边的孩子一定是最大的结点。
互不相同的原因:这是搜索树,不是为了创建而创建的,所以有重复的值可以不用插。
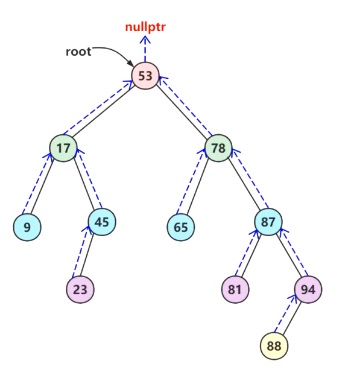
实际上二叉搜索树是个三叉链表,有指向左右孩子和双亲的三个指针,用于查找。
建立
结点结构
classBSTNode
{
public:
BSTNode():m_left(nullptr), m_right(nullptr) {}
BSTNode(int v):m_val(v),m_left(nullptr),m_right(nullptr) {}
int m_val;
BSTNode* m_left;
BSTNode* m_right;
};树建立
class BSTree
{
public:
BSTree():m_root(nullptr){}
void InsertValueST(int v)//插入
{
InsertValueBST(m_root, v);
}
void InsertValueBST(BSTNode*& root, int v);
void Print()//打印
{
InOrder(m_root);
cout << endl;
}
void InOrder(BSTNode* root);//中序遍历
BSTNode* SearchValue(int v)//查找
{
return SearchValue(m_root, v);
}
BSTNode* SearchValue(BSTNode* root, int v);
BSTNode* GetMax();//找最大
BSTNode* GetMin();//找最小
void DeleteValue(int v)//删除
{
DeleteValue(m_root, v);
}
void DeleteValue(BSTNode* &root, int v);
private:
BSTNode* m_root;
};输出
输出用中序遍历,按顺序输出
void Print()
{
InOrder(m_root);
cout << endl;
}
void InOrder(BSTNode* root);
void BSTree::InOrder(BSTNode* root)
{
if (root != nullptr)
{
InOrder(root->m_left);
cout << root->m_val << " ";
InOrder(root->m_right);
}
}查询
将当前根与key比较,如果等于则输出;如果小于则找左子树,否则找右子树;
非递归的查找
BstNode* FindValue(BSTree* tree,int v)
{
BstNode* p = tree;
while (p != nullptr && p->val != v)
{
p = v < p->val ? p->m_left : p->m_right;
}
return p;
}递归的查找
BSTNode* BSTree::SearchValue(BSTNode* root, int v)
{
if (root==nullptr)
return root;
if (v < root->m_val)
SearchValue(root->m_left, v);
else if(v>root->m_val)
SearchValue(root->m_right, v);
else if(v==root->m_val)
return root;
}注意: 每个结点的前驱是第一个左孩子的最右边的孩子,后继是第一个右孩子的最左侧的孩子(删除要用这个思想!!)
找最大、最小值
最大值:一直找右孩子,直到右为空是的结点为最大值;
最小值:一直找左孩子,直到左为空。
BSTNode* BSTree::GetMax()
{
BSTNode* p = m_root;
if (p != nullptr)
{
while (p->m_right != nullptr)
p = p->m_right;
}
return p;
}
BSTNode* BSTree::GetMin()
{
BSTNode* p = m_root;
if (p != nullptr)
{
while (p->m_left != nullptr)
p = p->m_left;
}
return p;
}删除!!!
创建一个t指向结点的指针temp
当根不为空:
若值比根小,递归在左边删
若值比根大,递归在右边删
若key等于当前结点值
若根有左右孩子
使temp指向根第一个左子树的最右边,或第一个右子树的最左边,将root的值换成temp指向的,删temp;
若只有一个孩子或没有孩子
让temp=root,root指向其唯一的孩子(或空),删除temp
void BSTree::DeleteValue(BSTNode* &root, int v)
{
BSTNode* temp = nullptr;
if (root != nullptr)
{
if (v < root->m_val)
DeleteValue(root->m_left, v);
else if (v > root->m_val)
DeleteValue(root->m_right, v);
else if (root->m_left != nullptr && root->m_right != nullptr)
{
temp = root->m_left;
while (temp->m_right != nullptr)
temp = temp->m_right;
root->m_val = temp->m_val;
DeleteValue(root->m_left, root->m_val);
}
else
{
temp = root;
if (root->m_right != nullptr)
root = root->m_right;
else
root = root->m_left;
delete(temp);
temp = nullptr;
}
}
}测试:
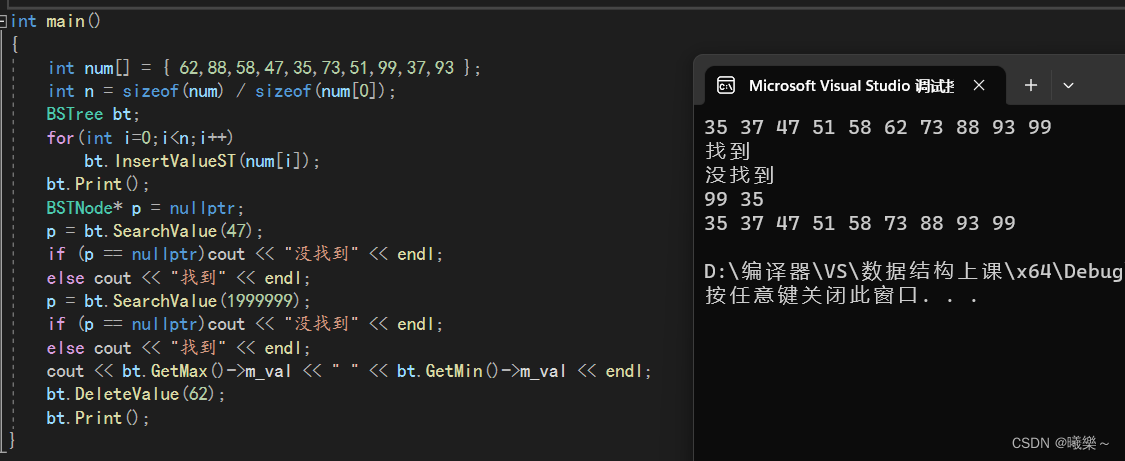
int main()
{
int num[] = { 62,88,58,47,35,73,51,99,37,93 };
int n = sizeof(num) / sizeof(num[0]);
BSTree bt;
for(int i=0;i<n;i++)
bt.InsertValueST(num[i]);
bt.Print();
BSTNode* p = nullptr;
p = bt.SearchValue(47);
if (p == nullptr)cout << "没找到" << endl;
else cout << "找到" << endl;
p = bt.SearchValue(1999999);
if (p == nullptr)cout << "没找到" << endl;
else cout << "找到" << endl;
cout << bt.GetMax()->m_val << " " << bt.GetMin()->m_val << endl;
bt.DeleteValue(62);
bt.Print();
}