110. 平衡二叉树【75】

news2024/11/14 3:09:24

难度等级：容易

上一篇算法：

102. 二叉树的层序遍历【206】

力扣此题地址：

110. 平衡二叉树 - 力扣（Leetcode）

1.题目：110. 平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

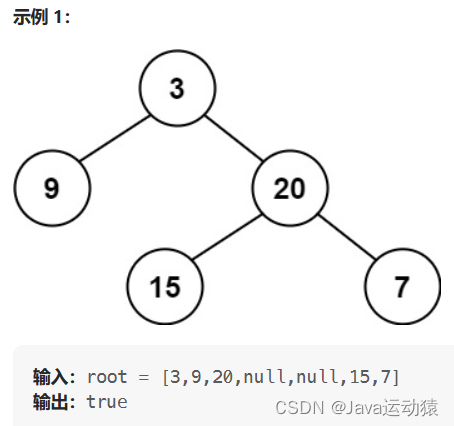
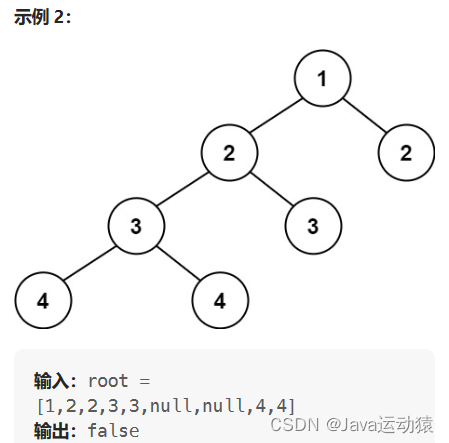
2.解题思路：

自底至顶：思路是对二叉树做先序遍历，从底至顶返回子树的最大高度，若判定某子树不是平衡树则“剪枝”，直接向上返回。

（判断子树是否满足平衡，子树不满足则直接返回，若子树满足，则继续向上比较，用递归的方式依次类推，直到判断根节点的左右子树是否满足平衡。）

算法流程：

递归返回值：

（1）当结点 root 的左/右子树的高度差<2 :则返回以节点root为根节点的子树的最大高度，即结点root的左右子树中最大的高度加1（max（left，right）+1）

（2）当结点 root 的左/右子树的高度差>=2 ：则返回 -1，代表此子树不是平衡树

递归终止条件：

（1）当越过叶子结点时，返回高度0；

（代码中：if（root==null）return 0；）root代表当前节点，而不只是根节点，因为是递归，所以一直在调用。

（2）当左（右）子树高度left == -1时，代表此子树的左（右）子树不是平衡树，因此直接返回-1

isBalanced（root）：

返回值：若 recur（root）!= 1，则说明此树平衡，返回true，否则返回false

思路参考：

110. 平衡二叉树 - 力扣（Leetcode）

3.代码实现：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        return recur(root) != -1;
    }

    private int recur(TreeNode root) {
        if (root == null) return 0;
        int left = recur(root.left);
        if(left == -1) return -1;
        int right = recur(root.right);
        if(right == -1) return -1;
        return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
    }
}