作者🕵️‍♂️：让机器理解语言か

专栏🎇：机器学习sklearn

描述🎨：本专栏主要分享博主学习机器学习的笔记和一些心得体会。

寄语💓：🐾没有白走的路，每一步都算数！🐾

0、介绍💬

监督学习（英语：Supervised learning）是机器学习中最为常见、应用最为广泛的分支之一。本次实验将带你了解监督学习中较为基础的线性模型，并学会使用 scikit-learn 来构建预测模型，用于解决实际问题。

知识点

线性回归模型
感知机分类模型

1、线性回归模型

scikit-learn 中包含的线性模型有最小二乘回归、感知机、逻辑回归、岭回归，贝叶斯回归等，由 sklearn.linear_model 模块导入。对于线性模型而言，即通过拟合线性函数（下式）去完成样本分类或回归预测。

$y(w,x)=w_0+w_1*x_1+...+w_p*x_p$

其中，最小二乘回归、岭回归、贝叶斯回归等是用于解决回归问题。而感知机、逻辑回归被用于解决分类问题。

这里，我们从比较基础的最小二乘法回归说起。最小二乘法是线性回归中最经典的方法之一，最小二乘的取名即来自于其选择了平方损失函数。在 scikit-learn 中，最小二乘法的实现方法如下：

名称	方法
最小二乘回归	sklearn.linear_model.LinearRegression( )

使用 scikit-learn 去解决一个机器学习相关的问题时，我们的代码都大同小异，主要是由三步走组成：

调用一个机器学习方法构建相应的模型 model，并设置模型参数。
使用该机器学习模型提供的 model.fit() 方法训练模型。
使用该机器学习模型提供的 model.predict() 方法用于预测。

请注意，上面的 3 个步骤大家多读几遍增强印象，后续我们就可以遵循这 3 步走的套路使用 scikit-learn 完成各类算法的建模了。

下面，我们尝试通过最小二乘回归去拟合二维平面上的一些点。首先，执行上面的第一步，载入方法并构建模型。

import warnings
from sklearn.linear_model import LinearRegression

# 忽略代码警告，仅供教学方便，自行书写代码时警告也很重要，不建议忽略
warnings.filterwarnings('ignore')

model = LinearRegression()  # 调用最小二乘法线性回归(第 1 步)
model
# 输出结果
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)

model 模型输出的参数，即为相应算法类的默认参数。当然，你可以参考官方文档中的说明来自定义参数。

接下来，使用模型带有的 fit() 方法去拟合 3 个点。三个点的特征向量分别为 [0,0], [1,1], [2,2]，对应的目标值为 [1,2,3]。

model.fit([[0, 0], [1, 1], [2, 2]], [1, 2, 3])  # 模型训练(第 2 步)
# 输出结果：
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

当然，我们也可以从这一步看到模型返回的参数。

训练时，选择的 [0,0]， [1,1]， [2,2] 这三个点恰好在一条直线上，再结合目标值想象一下它们的空间位置关系。我们可以使用下面的方法，输出拟合直线 w 项和常数项值。

model.coef_, model.intercept_
# (array([0.5, 0.5]), 1.0000000000000002)

如上所示，即实验拟合的函数应该为：

$y(x)=0.5 \times x_{1}+0.5 \times x_{2}+1$

当我们输入新的数值，例如 [3,3] 时，根据上面的函数，因变量的值为 4。那么，我们使用模型来预测，看一看结果是否为 4。

model.predict([[3, 3]])  # 模型预测(第 3 步)
# array([4.])

结果的确和我们预想的一致，也标志着我们通过 scikit-learn 完成了一个基础的线性回归问题，而建模的过程仅仅需要简单的 3 步。

上面的例子比较简单，下面我们导入 scikit-learn 内置的 diabetes 糖尿病数据集来训练一个复杂一点的最小二乘回归模型。

第一步：导入数据，并将其划分为 70% 的训练集和 30% 的测试集。机器学习中，我们习惯采用这样的比例来划分训练集和测试集。其中训练集用来训练模型，而测试集则用来评估模型的质量。测试集的数据不会出现在训练数据中，这也就类似我们使用了新的数据对训练好的模型进行预测和评估，以保证模型质量真实可靠。

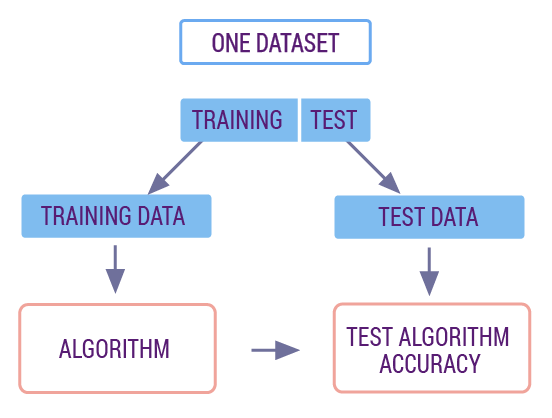
下面，我们会使用到 scikit-learn 提供的数据集切分函数 train_test_split。

from sklearn import datasets  # 导入内置数据集模块
from sklearn.model_selection import train_test_split  # 导入数据集切分模块
import numpy as np  # 导入数值计算模块

diabetes = datasets.load_diabetes()  # 载入糖尿病数据集

diabetes_feature = diabetes.data[:, np.newaxis, 2]  # 该数据集的特征较多，这里只选取其中一个
diabetes_target = diabetes.target  # 设定目标值

# 切分数据集为 70% 的训练集和 30% 的预测集
# random_state 随机数种子用于保证每次执行结果一致
train_feature, test_feature, train_target, test_target = train_test_split(
    diabetes_feature, diabetes_target, test_size=0.3, random_state=56)

第二步：载入最小二乘回归模型，并训练数据。这一步想必通过上面的例子已经清楚了，注意这里传入的是训练数据。

model = LinearRegression()  # 构建最小二乘线性回归模型
model.fit(train_feature, train_target)  # 使用训练集数据训练模型
# LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

第三步：使用测试集进行预测，并将结果绘图。

import matplotlib.pyplot as plt  # 导入 matplotlib 绘图模块
%matplotlib inline

# 绘图
plt.scatter(train_feature, train_target,  color='black')  # 绘制训练集散点图
plt.scatter(test_feature, test_target,  color='red')  # 绘制测试集散点图
plt.plot(test_feature, model.predict(test_feature),
         color='blue', linewidth=3)  # 绘制拟合直线

# 绘制图例
plt.legend(('Fit line', 'Train Set', 'Test Set'), loc='lower right')
plt.title('LinearRegression Example')
# Text(0.5, 1.0, 'LinearRegression Example')

最后，我们可以通过绘制的图像，更加直观地看出采用最小二乘回归模型进行线性拟合的结果。

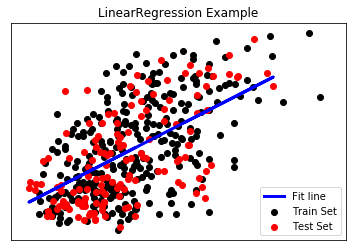
对于其他常见的线性回归模型，它们和最小二乘线性回归模型非常相似，只是采用了不同的损失函数。

例如，岭回归采用了带 L2 惩罚项的平方和损失函数。

$\min _{w}\|X w-y\|_{2}^{2}+\alpha\|w\|_{2}^{2}$

而另一种常见的 Lasso 回归，同样采用了带 L1 惩罚项的平方损失函数。

$\min _{w} \frac{1}{2 n_{\text {samples}}}\|X w-y\|_{2}^{2}+\alpha\|w\|_{1}$

下面列举了一些常见的广义线性回归模型，及它们在 scikit-learn 中对应的方法。

名称	方法
贝叶斯岭回归	sklearn.linear_model.BayesianRidge()
Lasso 回归	sklearn.linear_model.Lasso()
岭回归	sklearn.linear_model.Ridge()
随机梯度下降回归	sklearn.linear_model.SGDRegressor()
鲁棒回归	sklearn.linear_model.HuberRegressor()

这些方法相对于普通最小二乘回归模型而言，均增加了一些惩罚项。这样会提高模型的泛化能力，在实际应用中效果可能会好一些。

2、线性分类模型

除了线性回归，scikit-learn 还提供了一些解决线性分类的方法。其中，感知机就是非常有代表性的线性分类模型。

感知机是一个经典的二分类方法，由 Rosenblatt 于 1957 年时提出。它是神经网络和支持向量机的基础。感知机模型非常简单，输入为一些特征向量，输出则由正类和负类组成。而输入和输出之间，则是由符号函数连接。

$f(x)=\operatorname{sign}(w \cdot x+b) ; \operatorname{sign}(x)=\left\{\begin{array}{ll}{+1, x \geq 0} \\ {-1, x \leq 0}\end{array}\right.$

感知机的损失函数是错误分类点到分离超平面之间的距离总和，其学习策略同样也是损失函数最小化。

$\min \sum y(w \cdot x+b)$

在 scikit-learn 中，实现感知机通过调用 sklearn.linear_model.Perceptron()方法完成。下面，我们通过一个例子来展示感知机的分类过程。首先，使用 scikit-learn 提供的 make_classification 方法生成一组可被二分类的二维数组作为数据集。

from sklearn.datasets import make_classification  # 导入分类数据生成模块

# 随机生成一组可以被二分类的数据
X, y = make_classification(n_features=2, n_redundant=0,
                           n_informative=1, n_clusters_per_class=1, random_state=1)

X.shape, y.shape  # 查看数组形状
# ((100, 2), (100,))

这里，我们可以使用 Matplotlib 将该数据集绘制出来。

plt.scatter(X[:, 0], X[:, 1], marker='o', c=y)  # 绘制数据集散点图
# <matplotlib.collections.PathCollection at 0x7fffc2c25c10>

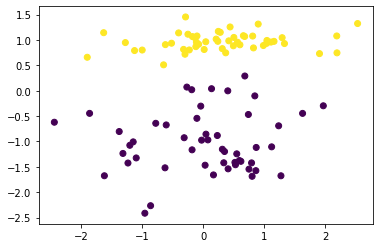
其中，y 即相当于人为给数据添加的标签。

我们可以看到，数据集分为 2 种颜色的样本点，并呈现出明显的线性界线。接下来，我们使用感知机对该数据集进行分类训练。

from sklearn.linear_model import Perceptron

# 将数据集划分为 70% 训练集和 30% 测试集
train_feature, test_feature, train_target, test_target = train_test_split(
    X, y, test_size=0.3, random_state=56)
# 建立感知机模型，使用默认参数
model = Perceptron()
# 使用训练集训练模型
model.fit(train_feature, train_target)

# Perceptron(alpha=0.0001, class_weight=None, early_stopping=False, eta0=1.0,
#            fit_intercept=True, max_iter=1000, n_iter_no_change=5, n_jobs=None,
#            penalty=None, random_state=0, shuffle=True, tol=0.001,
#            validation_fraction=0.1, verbose=0, warm_start=False)

训练结束后，我们用测试数据进行预测。请注意，由于测试数据与训练数据完全不同，也是算法之前完全没有见过的数据。我们后续可以通过模型对测试数据的预测结果，然后与真实的结果进行比较，从而得到模型的分类准确度。

preds = model.predict(test_feature)  # 使用测试集预测

准确度表示正确预测的样本占全部样本的比例，是用于评估分类模型的常用指标之一，我们得到的 preds 是模型的预测结果，而真实结果为 test_target。接下来，可以通过 scikit-learn 提供的机器学习sklearn 计算出分类准确度。

from sklearn.metrics import accuracy_score

accuracy_score(test_target, preds)  # 先传入真实值，再传入预测值
# 1.0

返回的结果即是测试集预测分类准确度，如果为 1.0 则表示预测全部正确，分类准确度为 100%。下面，我们使用 Matplotlib 将训练数据和测试数据绘制在原图上，并绘制出感知机分类时的决策边界。

# 创建一个绘图矩阵方便显示决策边界线
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.02),
                     np.arange(y_min, y_max, 0.02))

fig, ax = plt.subplots()
# 绘制决策边界
Z = model.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
ax.contourf(xx, yy, Z, cmap=plt.cm.Paired)
# 绘制训练和测试数据
ax.scatter(train_feature[:, 0], train_feature[:, 1])
ax.scatter(test_feature[:, 0], test_feature[:, 1])

# <matplotlib.collections.PathCollection at 0x7fffc2b9cc50>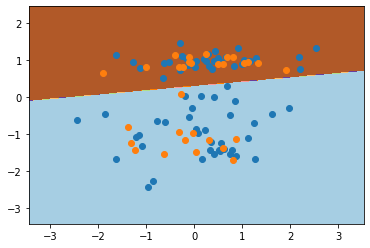

现在，我们就完成了一个简单的感知机分类实验。可以看出来，对于二分类问题，感知机的预测效果还是很不错的。

小练习

尝试通过 make_classification() 方法随机生成 300 条可用于二分类的数据，并通过 sklearn.linear_model.LogisticRegression() 调用线性模型中的逻辑回归方法完成分类。最后通过 Matplotlib 将训练集和测试集绘制出来。