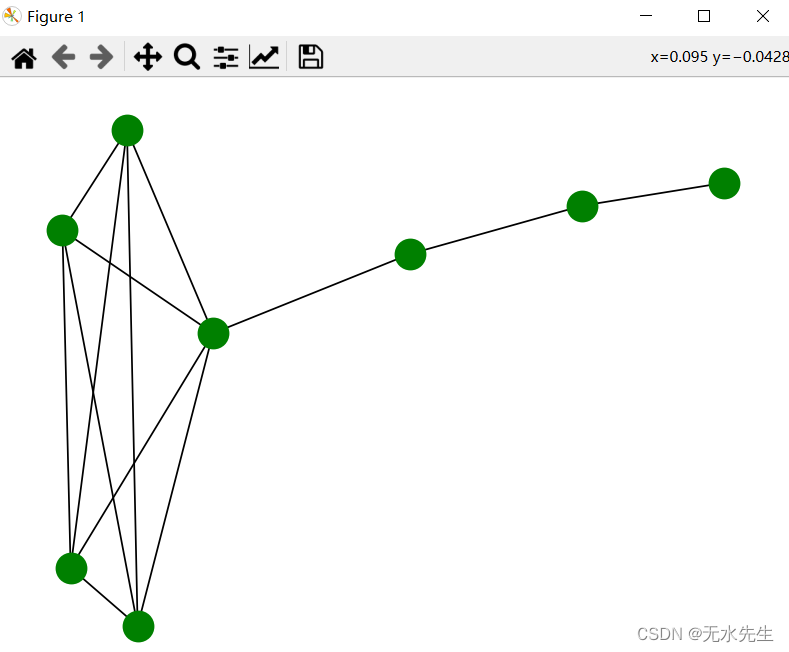
1. 单个特征（变量）的线性回归模型

• 房子的价格仅由房子的大小决定，如图：
  

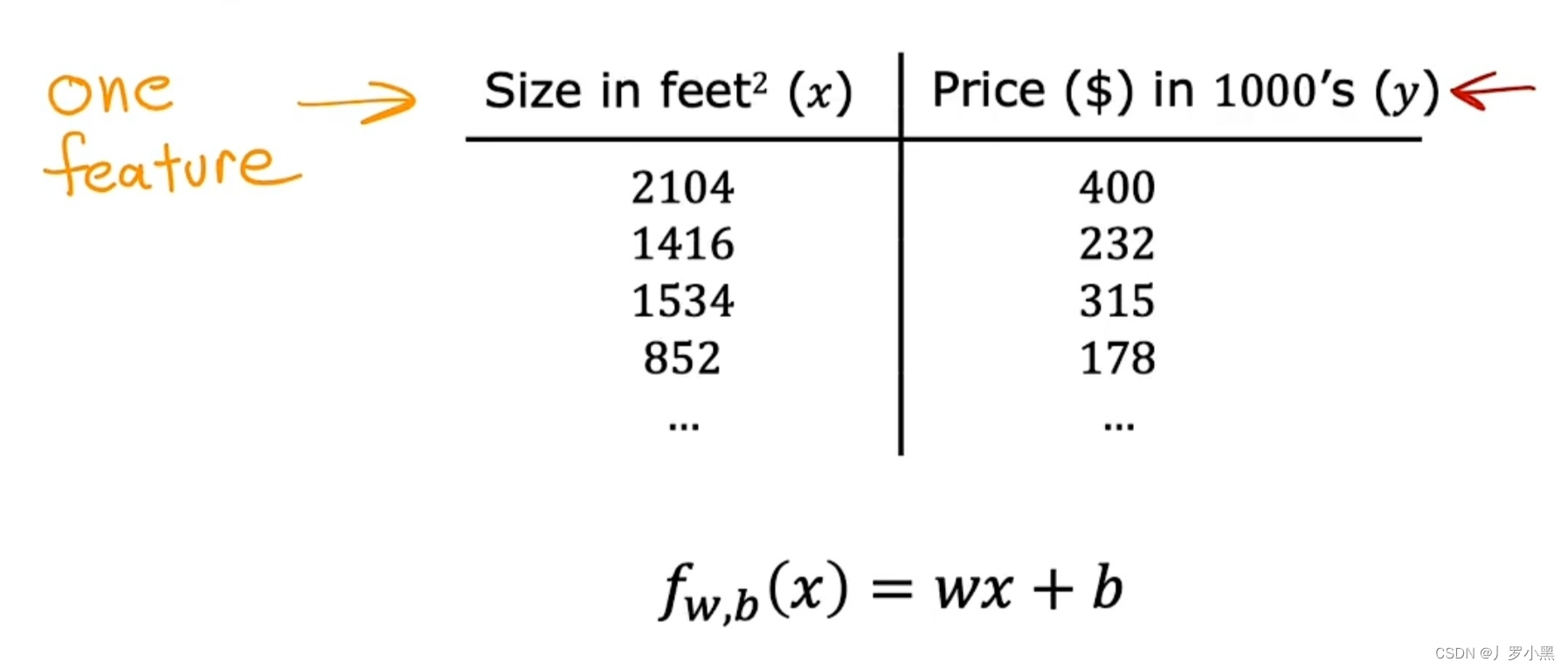
2. 多个特征（变量）的线性回归模型

• 房子的价格由房子的大小，房子有多少个卧室，房子有几层，房子住了多少年共同决定，如图：
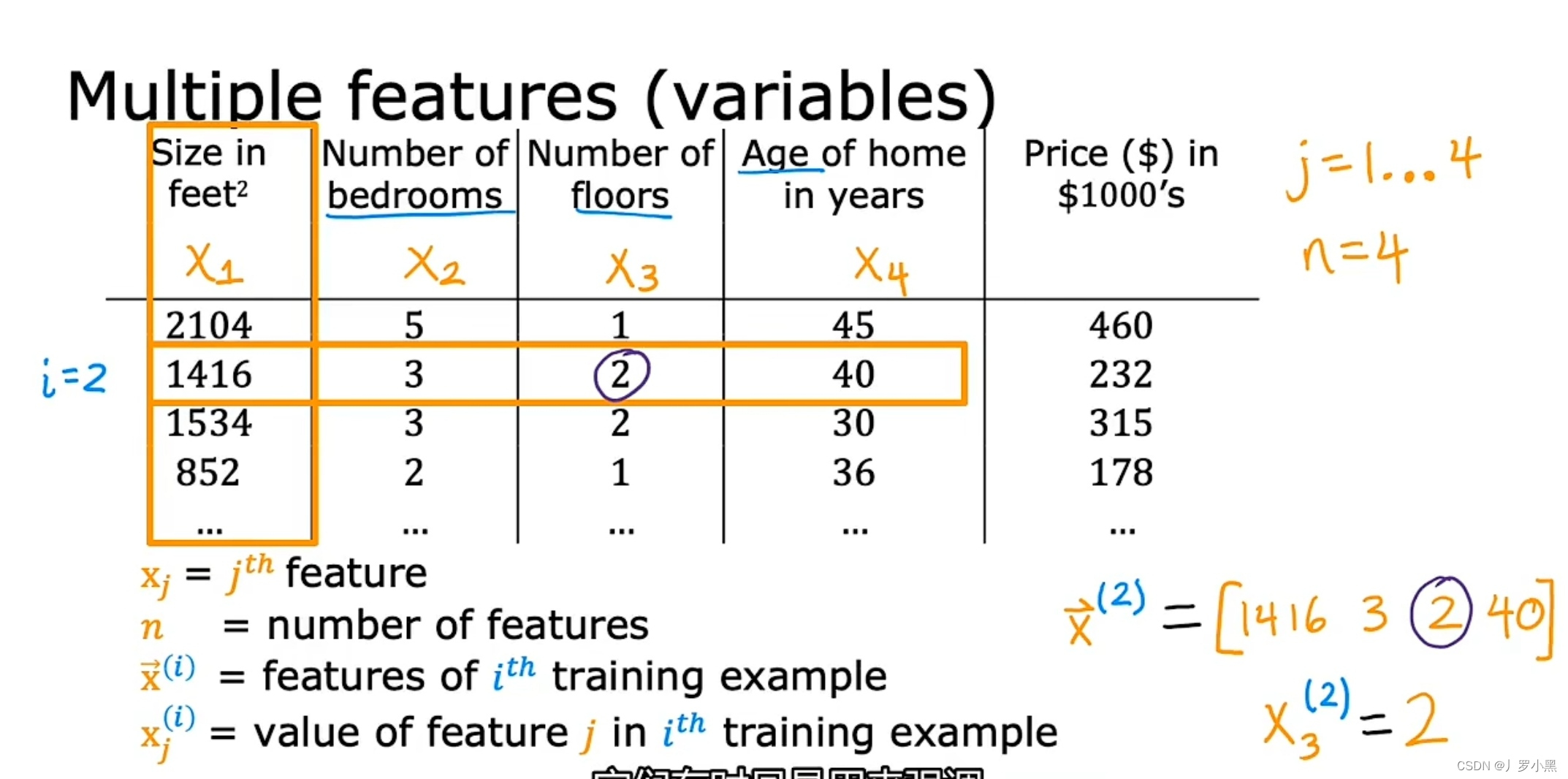
• x下标j：第j列特征（变量）
• n：特征（变量）的个数
• 向量x⁽ⁱ⁾：第i行的训练示例的所有特征（变量）
• x⁽ⁱ⁾下标j：第i行的训练示例的第j列特征（变量）
• 该例子的线性回归模型如图：
  
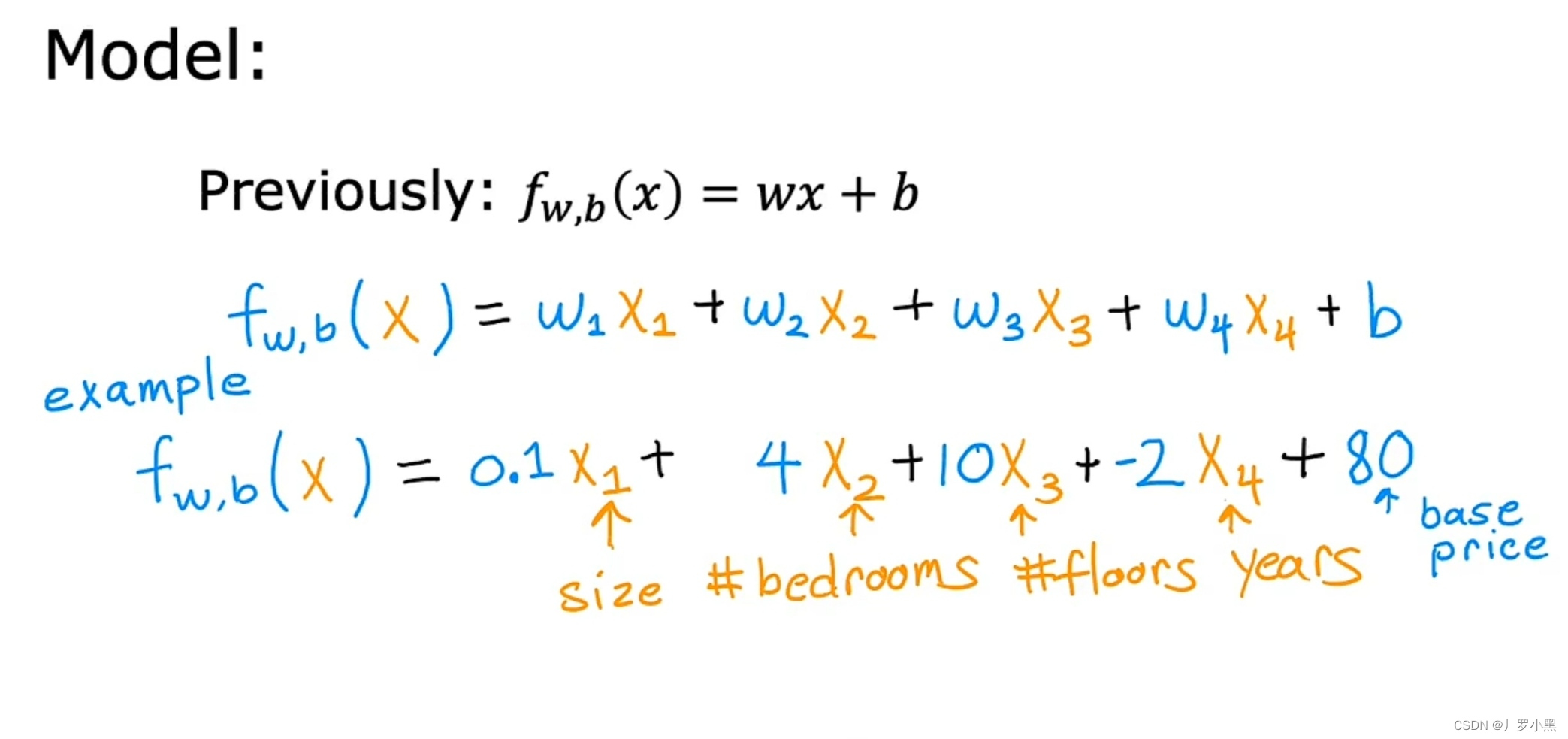
• 多元线性回归的每一个特征X都有对应的W，多元是指具有多个X

3. 多元线性回归模型及成本函数

• 通过向量的点积来简化有n个特征（变量）的多元线性回归模型，如图：
  
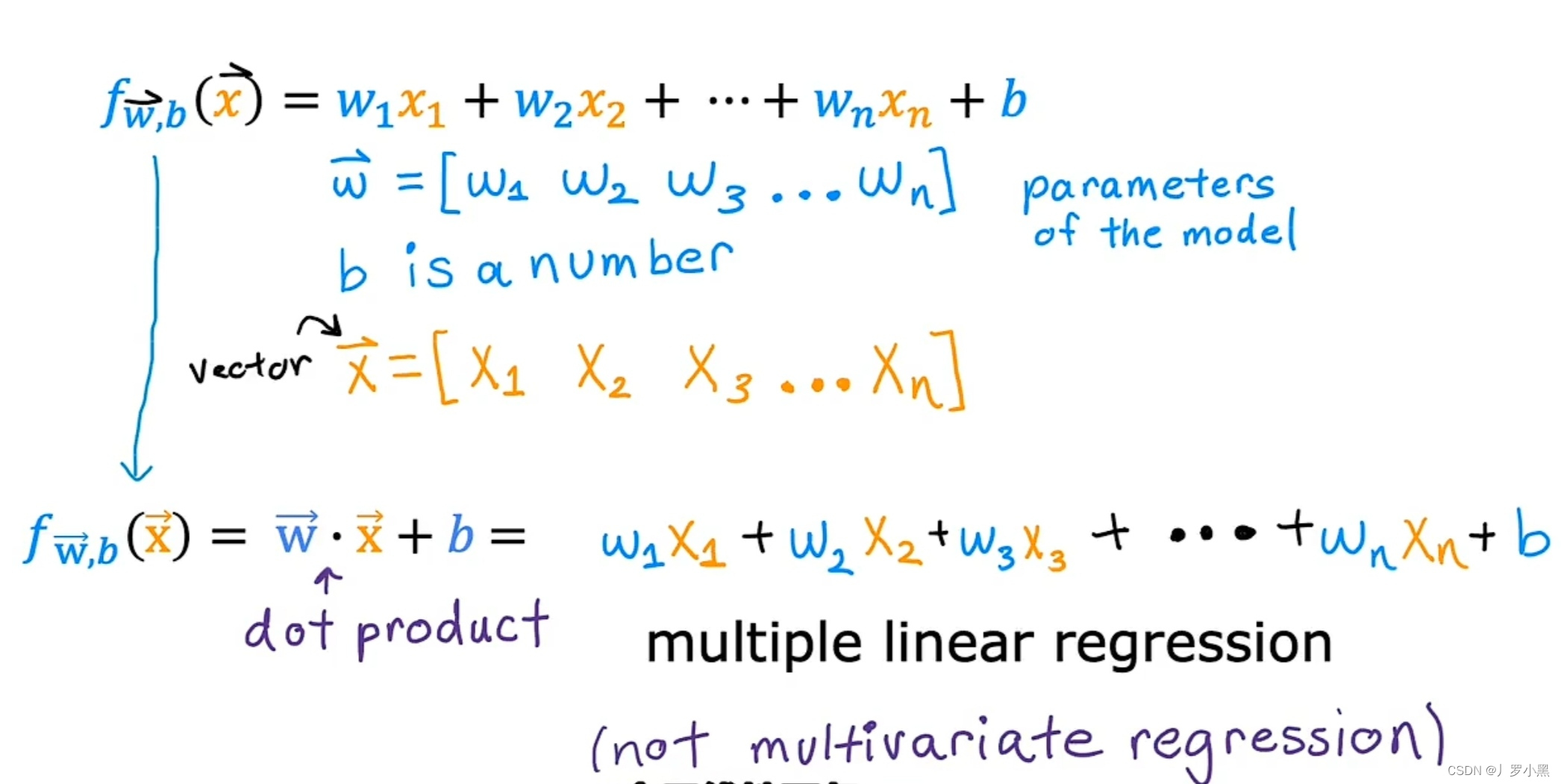
• 由上图可知，单元和多元线性回归的成本函数分别为：
  
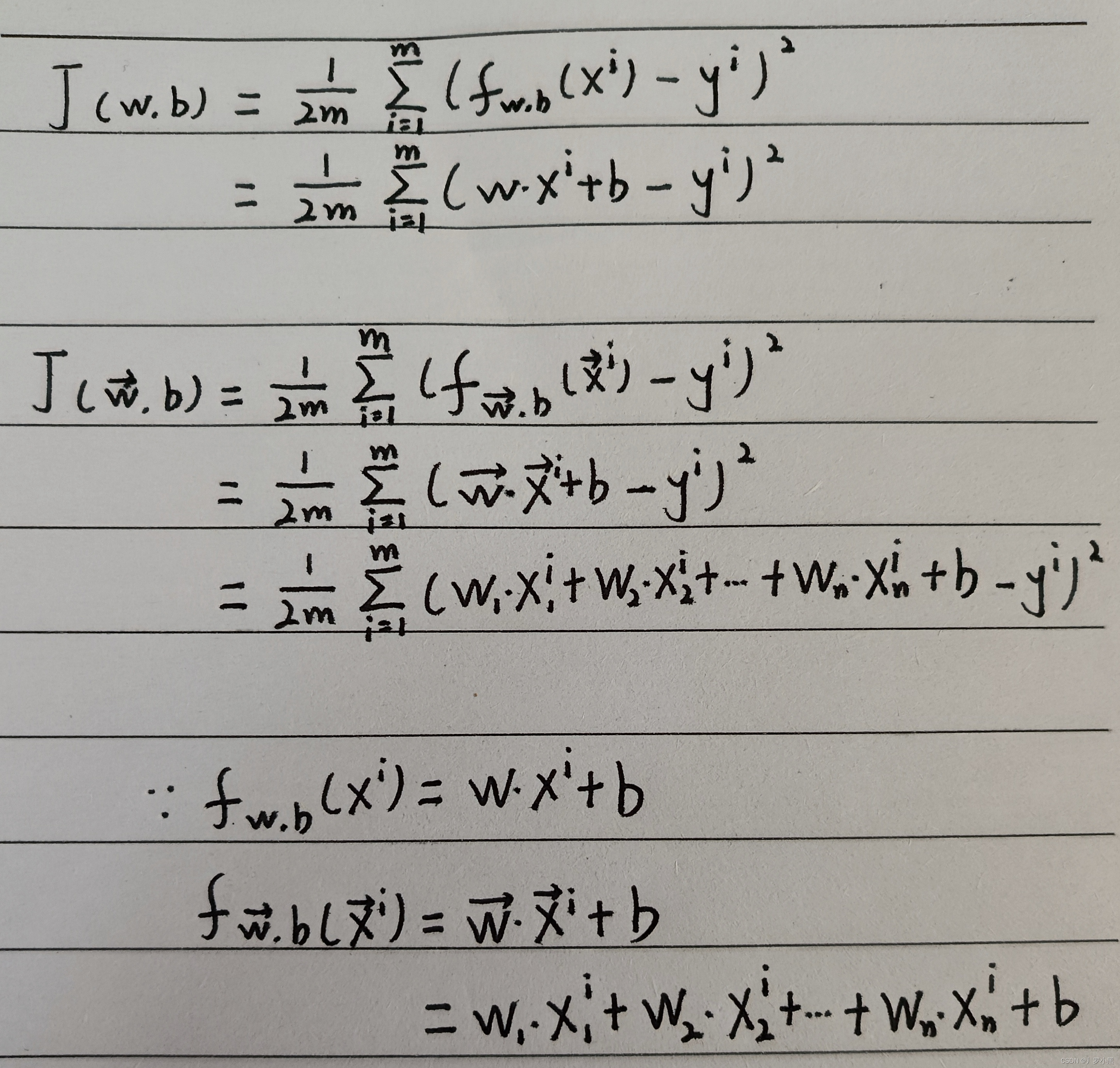
• dot product：向量的点积，如图：
  
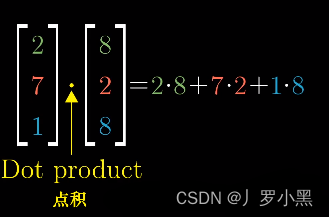
• multivariate regression：多元回归
• 这个模型是具有多个特征（变量）的线性回归，叫多元线性回归，不是多元回归

4. 向量化代码

• 向量化可以使代码更简洁，更容易编写，更容易阅读，运行也更高效。
• 向量化更高效的原因：NumPy（Python和机器学习中，最广泛的数值线性代数库）中的dot函数使用了并行硬件来提高效率，不论有没有GPU都行（GPU通常用于加速机器学习工作）
  
• 线性代数中，索引或计数是从1开始。代码的数组中，索引或计数是从0开始。
• 左下角的代码是顺序计算代码，效率很低，代码很长且重复
• 右上角的代码是for循环代码，效率很低，代码也不简洁。在Python中，range(0，n)表示，从0到n-1
• 右下角的代码是向量化代码，效率高，代码简洁

5. 向量化是怎么实现高效率的？

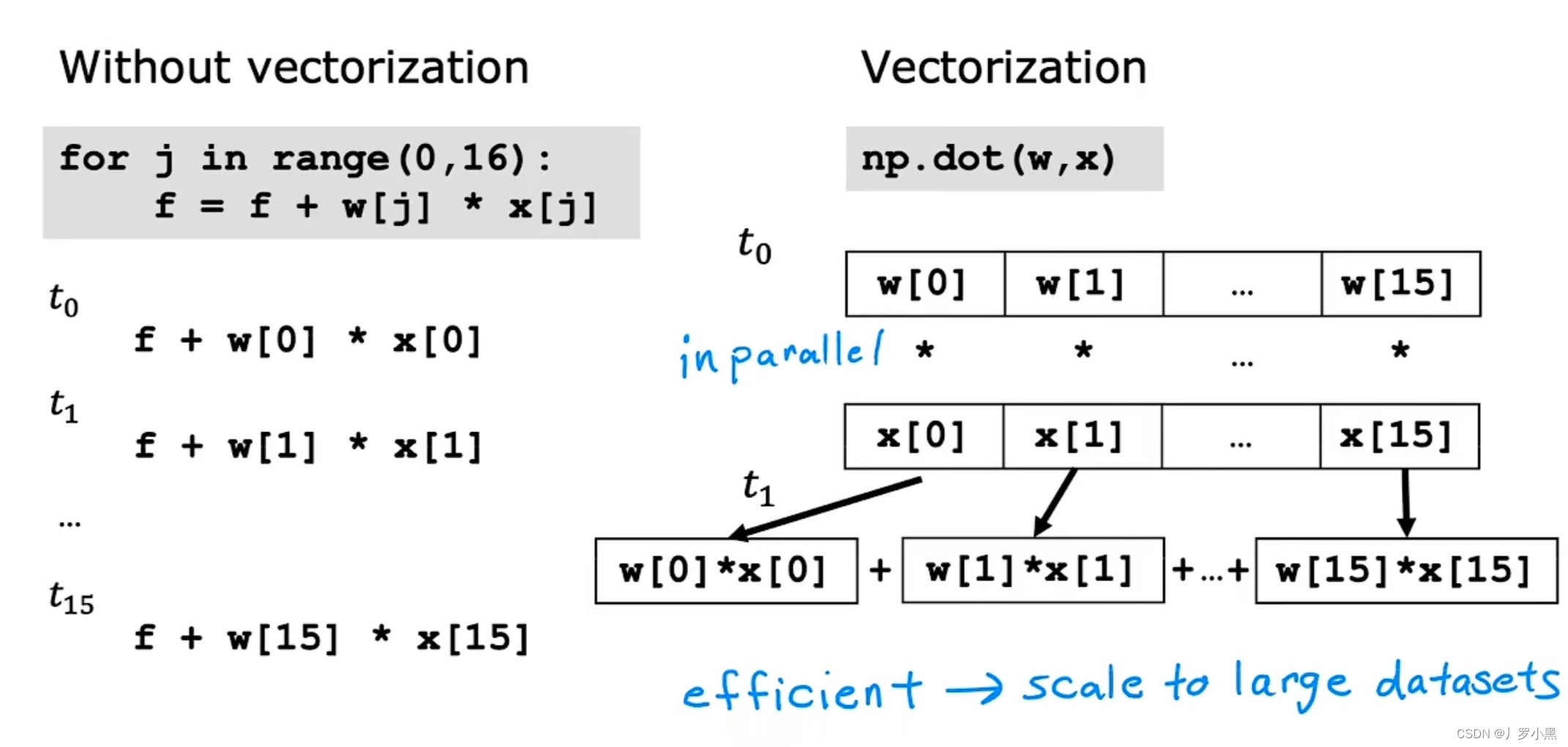
• 左边的for循环代码是不使用向量化的，计算机只会一步一步的执行，即在每一个时间戳上只会计算一次
• 右边的向量化代码，计算机第一步就会同时并行的将每对w和x相乘，第二步会获取这16个数据，并用专门的硬件非常高效的求和，并不需要一步一步把这16个数据加起来
• 这就表示，向量化的代码可以比没有向量化的代码，在更短的时间内进行计算。通常用于现代机器学习算法的大型数据集
• 例如，向量化在多元线性回归的梯度下降算法中的应用，向量d存放的是导数，0.1是学习率α，且忽略参数b：

• 左边的是不使用向量化的for循环代码
• 右边的是向量化代码，计算机在一个时间戳上执行一步操作：获取向量w中所有的值，并同时并行减去向量d中所有的值的0.1倍，最后将所有结果，在同一时间，并行的，一步回到向量w对应的位置上