ggrcs 包2.4版本已经发布一段时间了,大概几个月了吧,收到不少好评,
没听说太大的问题,最主要的问题有两个:
1.是说变量不是数字变量。

2.是说数据超过10万,无法处理

第一个问题非常好处理,这个问题是RMS包的报错,主要是数据格式必须是data.frame,不是这个格式容易报错,我们导入数据的时候最好以csv格式读入,这个格式比较稳定,不容易出错,如果你是其他格式导入的,可以使用as.data.frame()把它进行强制转换就可以了,在后面的版本中我也会对它进行强制转换。
第二个问题是数据量太大超过10万个,rms包的函数处理不了,就会报错,我们可以改一下公式给它生成一个模拟数据,画出来的RCS图和原始数据差不多,但是这样直方图就会和原始数据的不一样,这个暂时没有很好的办法解决,别人的R包我们改不了。
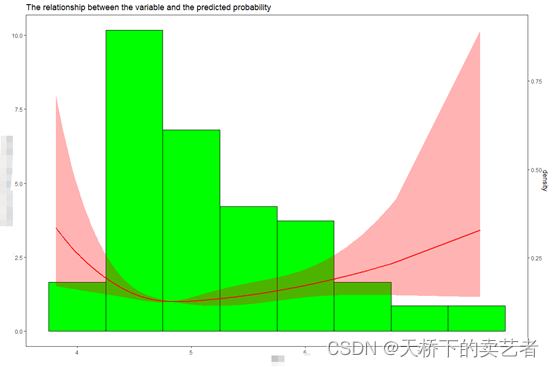
第三个其实不算问题,就是粉丝画出来的图不怎么好看,下图
library(ggrcs)
fit <- coxph(Surv(y1t,y1==1)~x1+age+gender,data = mydata)
ggrcs(mydata,fit,"x1")
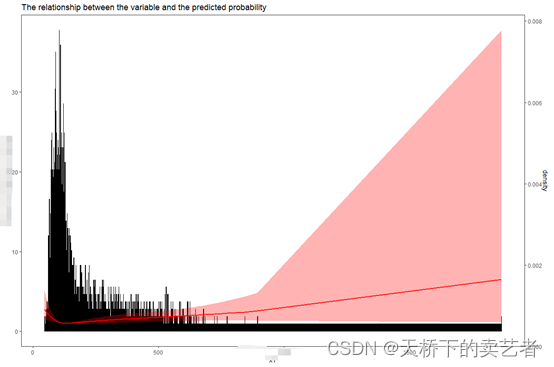
造成这个原因是数据造成的,这个不是正态分布,而是泊松分布,分布过于集中所致,我们只要对它的x变量取个对数,转换一下,让它变成正态分布,从新做图,变成如下
mydata$x99<-log(mydata$x1)
fit2 <- cph(Surv(y1t,y1==1) ~ rcs(x99,4)+age+gender, x=TRUE, y=TRUE,data=mydata)
ggrcs(mydata,fit2,"x99",histbinwidth=0.5)
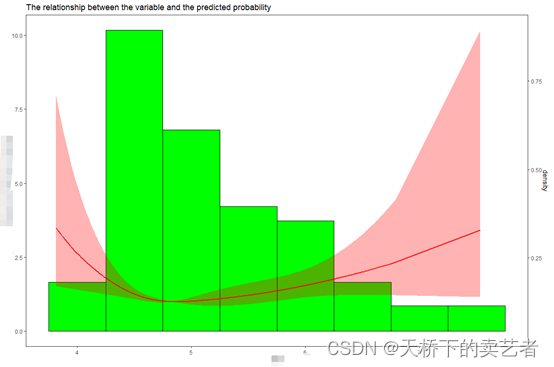
另外一个例子也是一模一样的,做的时候是下图,也不是正态分布
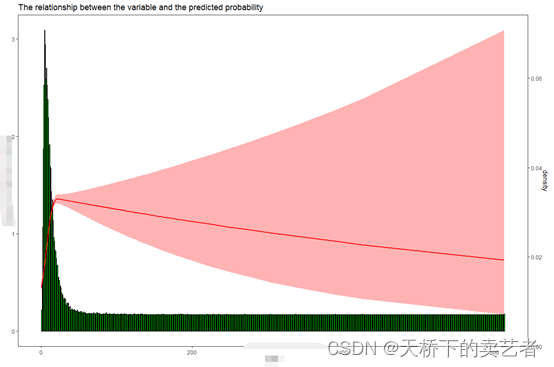
对x变量取对数以后,做图如下(代码就不贴了)
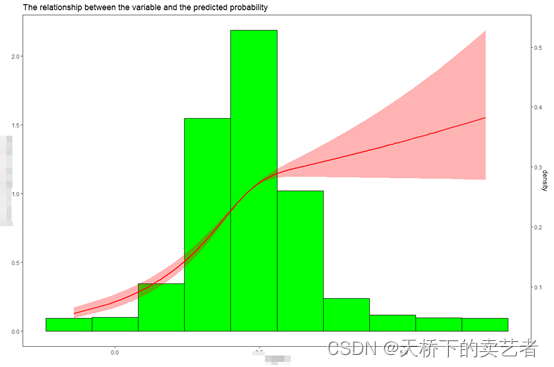
取对数后两个图的趋势都很明显,图也很漂亮,发个文章应该是没问题的。因此可以总结出,绘制直方图和RCS图,最好数据x是正态分布,如果偏态偏得太厉害,我们最好给它取个对数或者其他方法转换一下,让它变成近似正态分布。