目标级联分析法（ Analytical Target Cascading ， ATC ）理论matlab程序

目标级联分析法（Analytical Target Cascading，ATC）是一种采用并行思想解决复杂系统的设计方法，最初由密执安大学研究人员提出，主要用于汽车、飞机等设计领域。其原理如下：

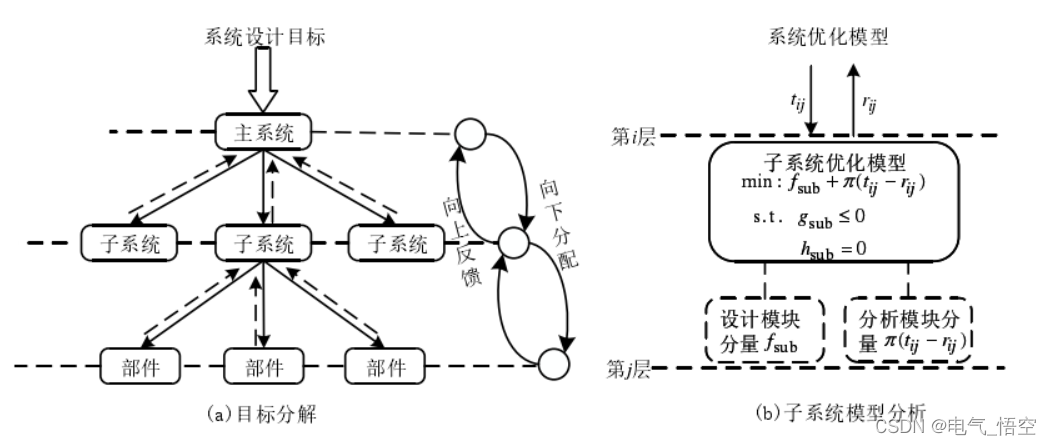
如图a所示，ATC 的基本思想是将设计指标自系统到子系统到部件不断分流，同时各级响应由下而上不断反馈，主系统、子系统和部件级各单元问题分别独立求解，交叠优化，直到满足收敛条件为止。每一个元素都是由一个分析模块和设计模块组成，如图 (b)所示。设计模块用于自身问题的优化设计，分析模块用于计算优化迭代时目标变量的响应值。系统将优化后的设计变量 t,ij 传递至子系统，这个值成为子系统的目标；子系统在不等式约束g,sub <=0 及等式约束h,sub = 0 的前提下，设计模块优化自身问题f,subf，分析模块通过引入惩罚项 pai( t,ij - r,ij)使设计模块优化的值 r,ij 靠近该目标。

惩罚项 pai( t,ij - r,ij) 代表复杂系统分解时耦合变量的一致性约束。常用的罚函数有二次罚函数、基于泰勒展开的对角线二次近似罚函数、拉格朗日罚函数及增广拉格朗日罚函数等。根据惩罚项表达式的不同，因此 ATC
有不同的数学表达形式，其求解效率也存在区别。

算例分析
初始目标函数：
求f(x1) = a1(x1-a2)^2最小值；
其中 x = [x1, x2]
约束条件：
g1(x) = b1x1 + b2x2 + b3 <= 0
g2(x) = c1x1 + c2x2 + c3 <= 0
其中
a = [2, 3];
b = [2, 4, 1];
c = [4, -1, 1];

转换成目标级联分析法（ Analytical Target Cascading ， ATC ）模型为：
1求P1 = f(x1_1) + phi_1(x1_1,x1_2,v,w)最小值
其中 x1_2, v, w 是固定参数, phi_1是增广拉格朗日罚函数
2求P2 = phi_2(x1_1,x1_2,v,w)最小值
其中x1_1, v, w 是固定参数, phi_2是增广拉格朗日罚函数
约束条件:
g1(x) <= 0
g2(x) <= 0

matlab部分程序：
ATC 目标级联分析法matlab程序

// 目标级联分析法matlab程序
%% 参数设置
v = [0 0];
w = [1 1];
beta = 1.3;% 罚函数乘子
z0 = -0.3;%初始值
c_old = [inf inf];
epsilon = 1e-4; % 收敛精度
continue_loop = 1;
maxiter = 100; %目标级联分析法的最大迭代次数
i = 1;

%% 外环
while continue_loop
    [c,x,f] = ATCinnerloop(v,w,z0);    
    v = v + 2*w.*w.*c;%更新一次惩罚因子
    w = w*beta;       %更新二次惩罚因子
    z0 = x(1);    
    if norm(c-c_old) <= epsilon   %范数norm
        if norm(c) <= epsilon
            continue_loop = 0;
        end
    end    
    c_old = c;   
    ...........略 

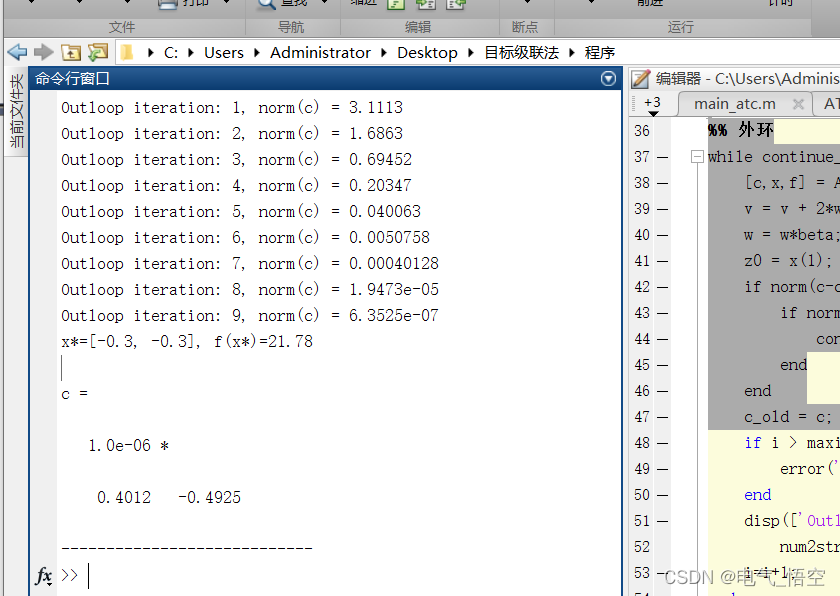
计算结果：