---

一、哈希表积累

什么时候想到用哈希法：当要需要查询一个元素是否出现过、判断一个元素是否出现在集合中时，考虑哈希法。

1.1 哈希map

1、遍历哈希映射代码

unordered_map<int,int> visited;
for (auto it = visited.begin(); it != visited.end(); ++it){
	if ((*it).first == key)
		(*it).second = value;
}

2、寻找哈希映射是否有某一个key值
if(visited.find(temp) != visited.end()) {...} // 说明找到了temp
3、哈希map中key相同的情况
unordered_map<int, int> mymap;
mymap[1] = 1;
mymap[1] = 2; // 这样1会被覆盖，此时mymap[1]为2
4、val为int时默认为0
unordered_map<int, int> mymap;
mymap[a + b]++; 这样是做是可以直接让 mymap[a+b]为1的

1.2 哈希set

1、遍历哈希set代码
for (auto it = windowfalse.begin(); it != windowfalse.end(); it++)
cout << *it << endl;
2、插入值进入哈希set代码

unordered_set<int> hash_set;
hash_set.insert(sum);

3、使用哈希set的erase函数会删除表中所有的相关数
windowfalse.erase(1); // 这会删除哈希set中所有的1，这么说是错的！因为哈希set永远不会有相同的元素！！
4、nums_set中的值为1、2，也就是说哈希set不会有相同的元素

vector<int> nums1 = {1,1,2,2};
unordered_set<int> nums_set(nums1.begin(), nums1.end());

5、查找哈希set是否有目标元素
hash_set.count(a) 找到了返回1
hash_set.find(sum) == hash_set.end() 找到了end()则说明没找到

二、哈希表基础

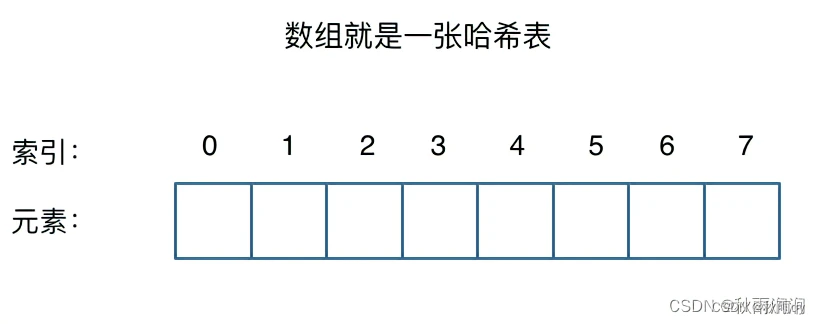
索引为key，元素为val，组成键值对
要枚举的话时间复杂度是O(n)，但如果**使用哈希表只需要O(1)**就可以做到。

三、题

3.1 242 有效的字母异位词

记住哈希表的遍历方式：

unordered_map<char,int> visited;

for (auto it = visited.begin(); it != visited.end(); ++it){
    if ((*it).second != 0)
        return false;
}

3.2 349 两个数组的交集

vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        vector<int> res;
        unordered_map<int,int> visited;
        for(int i=0; i < nums1.size(); i++){
            if(visited[nums1[i]] == 0)   // 重要！重复元素只加一次
                visited[nums1[i]]++;
        }
        for(int i=0; i < nums2.size(); i++){
            visited[nums2[i]]--;
            if(visited[nums2[i]] == 0)
                res.push_back(nums2[i]);
        }

        return res;
}

3.3 202 快乐数

重点：可能会无限循环，所以需要判断元素是否出现过，使用哈希set
unordered_set<int> hash_set;
hash_set.insert(sum) // 将值插入哈希set
if(hash_set.find(sum) != set.end()) {...} // 判断元素是否出现

class Solution {
public:

    int computesum(int n){
        int sum = 0;
        while(n)
        {
            int temp = n%10;
            n = n/10;
            sum += temp * temp;
        }
        return sum;
    }

    bool isHappy(int n) {
        int sum = 0;
        unordered_set<int> set;
        while(1){
            sum = computesum(n);
            if(sum == 1){
                return true;
            }
            if(set.find(sum) != set.end()){
                return false;
            }else{
                set.insert(sum);
            }
            n = sum;
        }
        
    }
};

3.4 1 两数之和

vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> visited;
        vector<int> res;
        for(int i=0; i < nums.size(); i++){
            //visited[nums[i]] = i;   // 放前面不行，通过不了[3,3]的用例
            int temp = target - nums[i];
            if((visited.find(temp) != visited.end()) && i > 0){
                res.push_back(i);
                res.push_back(visited[temp]);
                break;
            }
            visited[nums[i]] = i;   // 这个放后面，很弱智的逻辑问题
        }
        return res;
}

3.5 54 四数相加II

题目：给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0

用例1：
输入：nums1 = [1,2], nums2 = [-2,-1], nums3 = [-1,2], nums4 = [0,2]
输出：2
解释：
两个元组如下：

1. (0, 0, 0, 1) -> nums1[0] + nums2[0] + nums3[0] + nums4[1] = 1 + (-2) + (-1) + 2 = 0
2. (1, 1, 0, 0) -> nums1[1] + nums2[1] + nums3[0] + nums4[0] = 2 + (-1) + (-1) + 0 = 0

int fourSumCount(vector<int>& A, vector<int>& B, vector<int>& C, vector<int>& D) {
        unordered_map<int, int> umap; //key:a+b的数值，value:a+b数值出现的次数
        // 遍历大A和大B数组，统计两个数组元素之和，和出现的次数，放到map中
        for (int a : A) {
            for (int b : B) {
                umap[a + b]++;
            }
        }
        int count = 0; // 统计a+b+c+d = 0 出现的次数
        // 在遍历大C和大D数组，找到如果 0-(c+d) 在map中出现过的话，就把map中key对应的value也就是出现次数统计出来。
        for (int c : C) {
            for (int d : D) {
                if (umap.find(0 - (c + d)) != umap.end()) {
                    count += umap[0 - (c + d)];
                }
            }
        }
        return count;
    }

---