一、前言
我们前面简单的做了一个气温预测,经过反复调试,效果还不错。实际上在这个方向上我们还可以更进一步优化,但因为我们是学习嘛,主要还是看广度而不是深度。考虑到后面要开始学习卷积网络,我们必须把更基础的内容搞明白才行,比如神经网络到底是如何工作的,如果不搞明白后面卷积就只能说用法而不明白原因了。所以本篇我们从数学计算的角度来解读神经网络,方法是像前一篇那样构建一个最简单的网络,处理最简单的问题,然后手写一个“预测”函数,将整个预测的计算结果细化出来,并与TensorFlow预测结果进行比对。
二、最简单的神经网络
假设现在有输入X=[1,2,3],对应的Y=[2,5,6]。构建最简单的网络来训练。
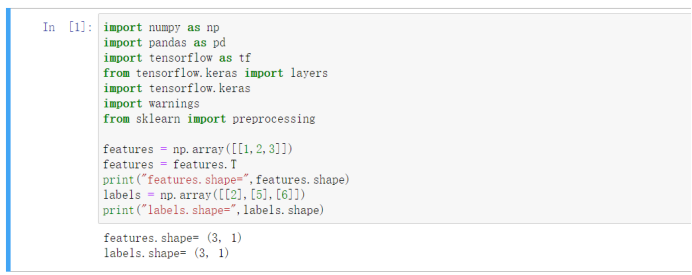
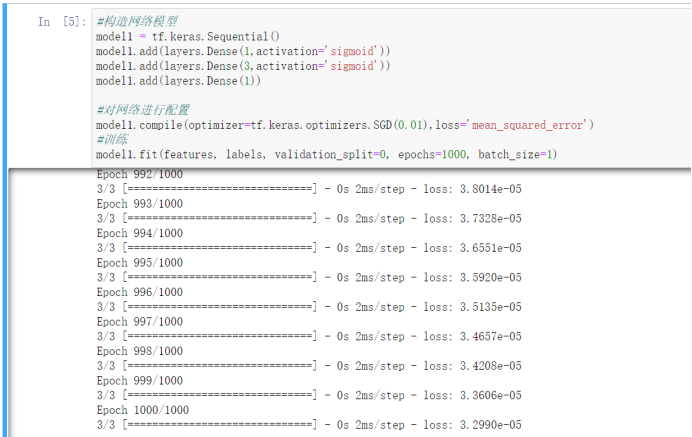
三、神经网络的权重参数
我们可以通过model.get_layer(index=n)来获取神经网络的任意一层,接着用layer.get_weights()获取到“权重参数”。
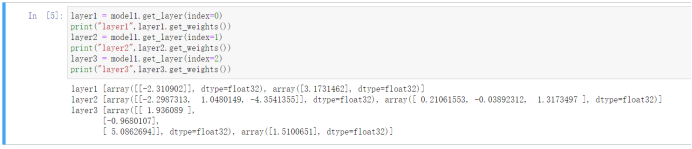
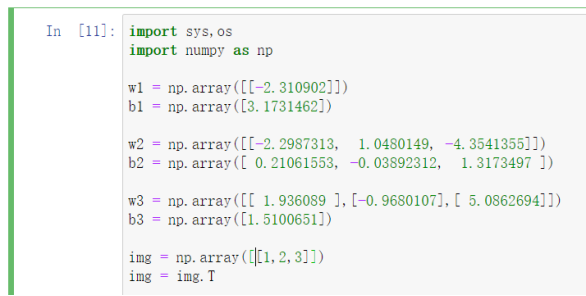
如上图所示,我们训练后神经网络的权重参数如下:
w1 = np.array([[-2.310902]])
b1 = np.array([3.1731462])
w2 = np.array([[-2.2987313, 1.0480149, -4.3541355]])
b2 = np.array([ 0.21061553, -0.03892312, 1.3173497 ])
w3 = np.array([[ 1.936089 ],[-0.9680107],[ 5.0862694]])
b3 = np.array([1.5100651])
可以说权重参数就是神经网络本身,所谓训练就是将权重参数从无序混乱的数字,“训练”成上面这样的看起来似乎还是挺乱的数据。但是我们可以直接拿来用,自己计算一下就明白了。
四、手写预测部分
神经网络的基本组成是“预测、损失计算、反向传播”,中间可能穿插激活函数、正则化等等。所谓预测其实就是基于权重参数进行一次矩阵计算,所谓损失计算就是用预测的结果与正确值进行比较,反向传播则是在损失的基础上对权重参数进行优化。这里我们自己手写一下预测部分,对原理感兴趣的可以翻翻我2019年写的神经元解析部分。
具体代码如下:
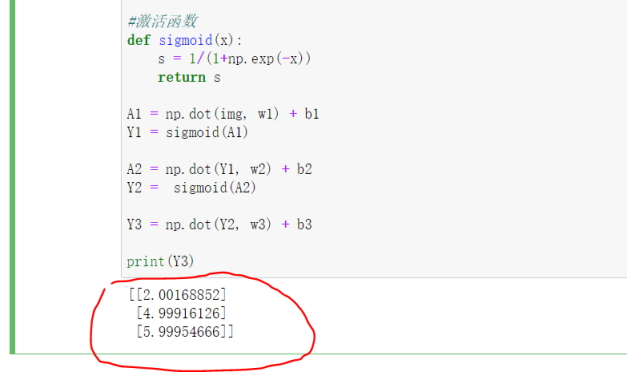
在上面的代码中,我们模拟构建了3层网络(1:3:1),每一层所谓网络实际就是一次np.dot()的计算,也就是矩阵的乘积。我们再看下神经网络的公式:
Y = F(X)+b
现在可以得知Dense(全连接)神经网络的公式就是:
Y = F(X)+b = np.dot(X, W)+b
另外需要注意的是激活函数sigmoid,在前面用TensorFlow构建网络时,我们使用了:
model1.add(layers.Dense(1,activation='sigmoid'))
model1.add(layers.Dense(3,activation='sigmoid'))
model1.add(layers.Dense(1))
所以这里在对Y进行计算后,需要再过一次激活函数。
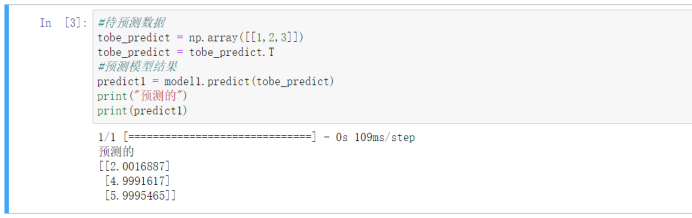
最后我们再看下计算的结果,发现是一模一样对吧,所以我们手写的是对的。
五、计算过程
自己手写的代码,好处就是我们可以拆解的很细,这里我们将每一步的计算结果都输出来。
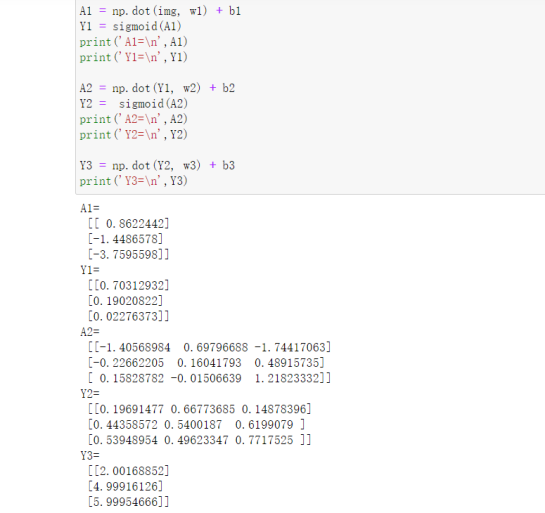
为方便理解我们在excel里整理下:

接下来,我们按神经网络的计算规则,从头到尾计算一遍。
1、第一层计算
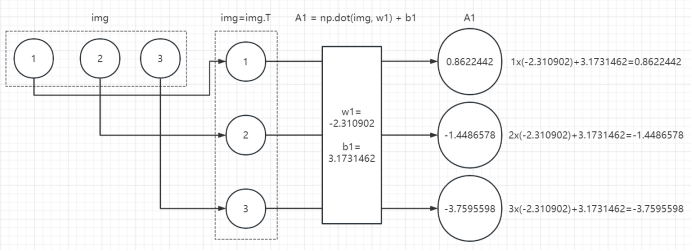
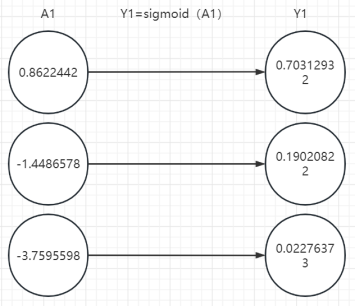
2、第二层计算
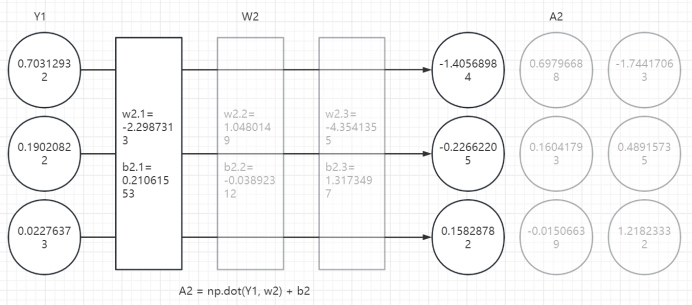
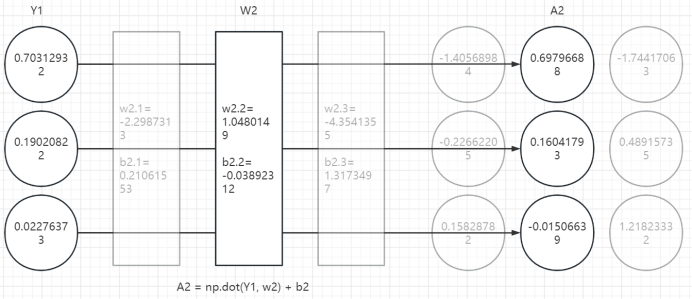
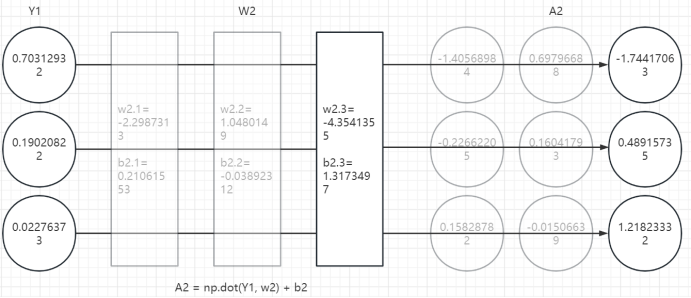
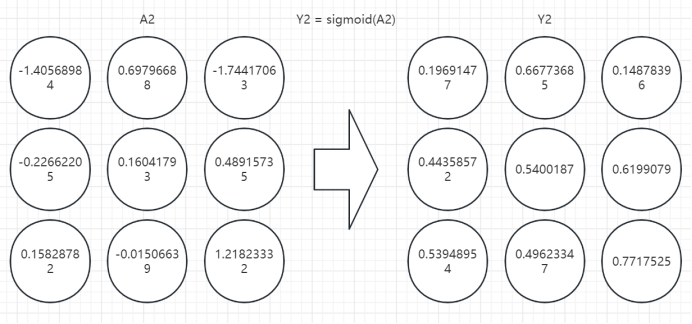
3、第三层计算
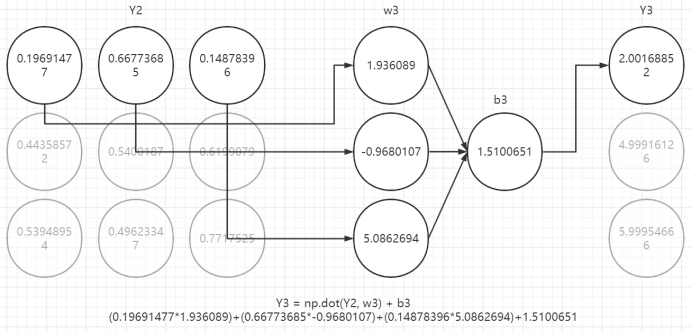
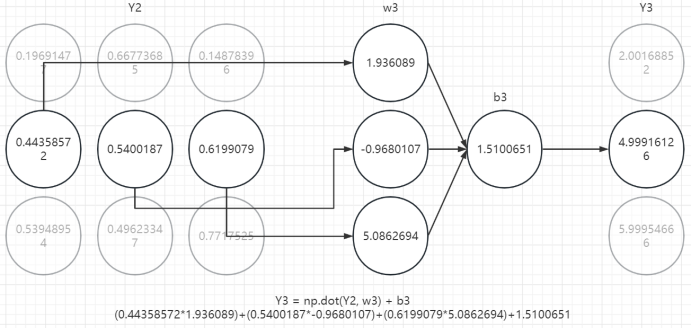
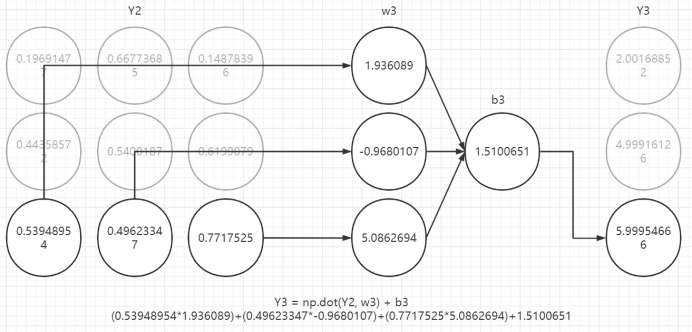
六、回顾
本篇我们在前面知识的基础上,对神经网络的计算原理进行了验证,结果还不错。而且还分别使用TensorFlow框架、原生python代码、数值计算进行了相互印证。
实际上所谓的深度学习和神经网络就是像前面我们演示的那要,是各种矩阵的计算。而神经网络本身也是由w和b组成的数字矩阵。但就是这样的简单计算最终实现了非常神奇的功能。不得不感叹,大道至简啊。
基于此,我想到,其实训练可能比较复杂,但训练好后的模型使用还是非常简单的,所以我们可以脱离TensorFlow的框架,在任意平台来应用训练好的模型,也可以针对性的对大矩阵的计算进行优化。