数轴上的bfs

农夫约翰被通知，他的一只奶牛逃逸了！所以他决定，马上出发，尽快把那只奶牛抓回来．

他们都站在数轴上．约翰在N(0≤N≤100000)处，奶牛在K(0≤K≤100000)处．约翰有

两种办法移动，步行和瞬移：步行每秒种可以让约翰从x处走到x+1或x-1处；而瞬移则可让他在1秒内从x处消失，在2x处出现．然而那只逃逸的奶牛，悲剧地没有发现自己的处境多么糟糕，正站在那儿一动不动．

那么，约翰需要多少时间抓住那只牛呢？

输入格式

* Line 1: Two space-separated integers: N and K

仅有两个整数N和K.

输出格式

* Line 1: The least amount of time, in minutes, it takes for Farmer John to catch the fugitive cow.

最短的时间．

样例

输入样例：

5 17
Farmer John starts at point 5 and the fugitive cow is at point 17.

输出样例：

4
OUTPUT DETAILS:

The fastest way for Farmer John to reach the fugitive cow is to
move along the following path: 5-10-9-18-17, which takes 4 minutes.

广搜 - -队列

每次取队头元素出队列，对于该队头节点，可能就是要求的节点，成功，退出；也可能不是，不是的话，利用该队头元素扩展与该节点有边相连且没有被访问的节点，将新的节点入队，直到队为空，所有图中相连的节点都被访问过。

使用队列：

手写队列，队列有两个指针-front和rear，对于这两个指针，操作都是+1就是上移，如果需要构造循环队列，则需要进行取余对队列长度queueLength进行操作，队列为空等价于front不等于rear，即队首队尾指针不同，稍微整理代码如下，

///普通队列
    #define MAXLENGTH 100000
    int que[MAXLENGTH + 50];

    int rear = 0;
	int front = 0;

    while (rear != front){

        que[rear] = 入队元素值;
		rear++;
        //出队
        front = front + 1;
}

进行循环队列
	#define MAXLENGTH 100000
    int que[MAXLENGTH];

    int rear = 0;
	int front = 0;

    while (rear != front){

        que[rear] = 入队元素值;
		rear=(rear+1)%MAXLENGTH;
        //出队
        front = (front + 1)%MAXLENGTH;
}

参考代码：

#include <stdio.h>
#define MAXLENGTH 100000
int que[MAXLENGTH + 50];
int flag[MAXLENGTH + 50];
int main() {
	//int dp[MAXLENGTH+50];

	int rear = 0;
	int front = 0;
	
	int s, t;
	scanf("%d %d", &s, &t);
	que[0] = s;
	//front=(front+1)%(MAXLENGTH+50);
	rear = rear + 1;
	flag[s] = 1;
	int i = s;
	int cnt = 0;
	while (rear != front) {
		if (flag[t] == 1) {
			printf("%d\n", cnt);
			return 0;
		}
		cnt++;//步数加一

		int loopf = front;
		int loopr = rear;
		for (int j = loopf; j != loopr; j++)
		{
			int tt = que[j];
			//在范围内且没有走过 
			if (tt * 2 <= MAXLENGTH && flag[tt * 2] == 0) {
				
				que[rear] = tt * 2;
				flag[tt * 2] = 1;rear++;
			}
			if (tt + 1 <= MAXLENGTH && flag[tt + 1] == 0) {
				
				que[rear] = tt + 1;
				flag[tt + 1] = 1;rear++;
			}

			if (tt - 1 >= 0 && flag[tt - 1] == 0) {
				
				que[rear] = tt - 1;
				flag[tt - 1] = 1;rear++;
			}
			front = front + 1;
		}


	}

	return 0;
}

如果不仅要输出所需时间，还需要输出路径，如何编程实现

设置每个点的前驱并进行记录

/*
Time Limit: 1000 ms
Memory Limit: 256 mb
农夫John的奶牛跑路了。将地图视作一条数轴，
John的初始位置在s而奶牛的位置在t(0<=s,t<=100000)。John可以花费一分钟的时间使自己作如下移动：

1 从点x移动到点x+1
2 从点x移动到点x-1
3 从点x移动到点x*2
奶牛的位置一直在点t。现在给定s,t，要求John要追上奶牛最少需要几分钟。
*/

#include <stdio.h>
#define MAXLENGTH 100000//设置最大的数
int que[MAXLENGTH + 50];//记录队列，用于bfs广度优先搜索
int flag[MAXLENGTH + 50];//记录是否走过，1表示走过，0表示未走过
int mapp[MAXLENGTH + 50];//记录前驱
int pathp[MAXLENGTH + 50];//记录路径，用于输出路径
int main() {
	//队尾指针
	int rear = 0;
	//队首指针
	int front = 0;
	
	int s, t;
	scanf("%d %d", &s, &t);
	que[0] = s;//起点入队
	//front=(front+1)%(MAXLENGTH+50);
	rear = rear + 1;//尾指针移动
	flag[s] = 1;//标记，该点已走过
	int cnt = 0;//计数，当前所走时间
	while (rear != front) {
		if (flag[t] == 1) {
			//到达终点，输出时间和路径
			//输出时间
			printf("%d\n", cnt);
			//路径转换--记录是前驱，需要先得到路径再逆序输出
			int tmp;
			tmp = t;
			//printf("%d<-", tmp);
			int itmp = 0;
			pathp[itmp] = tmp;
			itmp++;
			while (1) {
				if (mapp[tmp] == s)
				{
					//printf("%d", mapp[tmp]);
					pathp[itmp] = mapp[tmp];
					//itmp++;
					break;
				}
				else {
					//printf("%d<-", mapp[tmp]);
					pathp[itmp] = mapp[tmp];
					itmp++;
					tmp= mapp[tmp];
				}
			}
			//输出起点
			printf("%d", pathp[itmp]);//print s
			//输出路径，直到终点
			for (int j = itmp-1; j >= 0; j--) {
				printf("->%d", pathp[j]);//print s
			}
			return 0;
		}
		cnt++;//步数加一
		//记录当前队列队首队尾指针
		int loopf = front;
		int loopr = rear;
		//当前队列数据出队并压入新的数据
		for (int j = loopf; j != loopr; j++)
		{
			int tt = que[j];
			//在范围内且没有走过 
			if (tt - 1 >= 0 && flag[tt - 1] == 0) {

				que[rear] = tt - 1;//入队
				flag[tt - 1] = 1;//标记
				mapp[tt - 1] = tt;//前驱
				rear++;//入队
			}
			if (tt * 2 <= MAXLENGTH && flag[tt * 2] == 0) {
				
				que[rear] = tt * 2;//入队
				flag[tt * 2] = 1;//标记
				mapp[tt * 2] = tt;//前驱
				rear++;//入队
			}
			if (tt + 1 <= MAXLENGTH && flag[tt + 1] == 0) {
				
				que[rear] = tt + 1;//入队
				flag[tt + 1] = 1;//标记
				mapp[tt + 1] = tt;//前驱
				rear++;//入队
			}
			front = front + 1;//出队
		}
	}
	return 0;
}

二维平面上的bfs

定义一个二维数组：

int maze[5][5] = {

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,

};

它表示一个迷宫，其中的1表示墙壁，0表示可以走的路，只能横着走或竖着走，不能斜着走，要求编程序找出从左上角到右下角的最短路线。

输入：一个5 × 5的二维数组，表示一个迷宫。数据保证有唯一解。
输出：左上角到右下角的最短路径，格式如样例所示。
样例输入：

0, 1, 0, 0, 0,

0, 1, 0, 1, 0,

0, 0, 0, 0, 0,

0, 1, 1, 1, 0,

0, 0, 0, 1, 0,

复制
样例输出：
(0, 0)
(1, 0)
(2, 0)
(2, 1)
(2, 2)
(2, 3)
(2, 4)
(3, 4)
(4, 4)

提示：

在一个点访问完后，并且拓展出其周围全部的点后，并不能就丢弃，

而是应该储存起来；
然后通过下标，回溯寻找出路径。

输出路径，可以参考链表或者迪杰斯特拉算法等，对于一个点，设置其前继，即该点前面的点，由此可以得到路径。

#include<stdio.h>
int maze[10][10];
struct point {
	int x;
	int y;
};
struct point que[100];
int flag[10][10];//记录是否走过 
struct point  mapp[10][10];//记录(i,j)的前驱 
struct point path[100];//记录路径用于输出 

int main() {
	for (int i = 0; i < 5; i++)
		for (int j = 0; j < 5; j++) {
			scanf("%d,", &maze[i][j]);
		}
	int front = 0;
	int rear = 0;
	que[0].x = 0;//入队 
	que[0].y = 0;
	rear++;
	flag[0][0] = 1;//左上角点标记 
	int cnt = 0;
	while (1) {
		if (flag[4][4] == 1) {//到达终点 
			printf("路径长度是%d\n", cnt);
			//路径转换并输出 
			int pathcnt = 0;
			//path[0].x = 4;
			//path[0].y = 4;
			//pathcnt++;
			struct point pointtmp;
			pointtmp.x = 4;
			pointtmp.y = 4;

			while (1) {
				int tmppathx = pointtmp.x;
				int tmppathy = pointtmp.y;
				if (tmppathx == 0 && tmppathy == 0) {
					//到达起点 
					path[pathcnt].x = 0;
					path[pathcnt].y = 0;
					break;
				}
				else {//迭代 
					path[pathcnt].x = tmppathx;
					path[pathcnt].y = tmppathy;
					pathcnt++;//下标加一 
					pointtmp.x = mapp[tmppathx][tmppathy].x;
					pointtmp.y = mapp[tmppathx][tmppathy].y;
				}
			}
			//输出起点
			for (int printi = pathcnt; printi >= 0; printi--) {
				printf("(%d,%d)\n", path[printi].x, path[printi].y);
			}
			break;
		}
		cnt++;
		int rear_ = rear;
		int front_ = front;
		for (int i = front_; i != rear_; i++) {
			//寻找可能入队的
			int xtmp = que[i].x;
			int ytmp = que[i].y;
			int next[4][2] = { 1,0,0,1,-1,0,0,-1
			};
			for (int nexti = 0; nexti < 4; nexti++) {
				int nextx = xtmp + next[nexti][0];
				int nexty = ytmp + next[nexti][1];
				if (nextx < 5 && nexty < 5 && nextx >= 0 && nexty >= 0 && maze[nextx][nexty] == 0 && flag[nextx][nexty] == 0) {
					que[rear].x = nextx;//入队 
					que[rear].y = nexty;
					rear++;
					flag[nextx][nexty] = 1;//标记 
					mapp[nextx][nexty].x = xtmp;//记录前驱 
					mapp[nextx][nexty].y = ytmp;
				}
			}
			front++;//出队 
		}
	}
	return 0;
}

bfs

如图所示：有9只盘子，排成1个圆圈。其中8只盘子内装着8只蚱蜢，有一个是空盘。

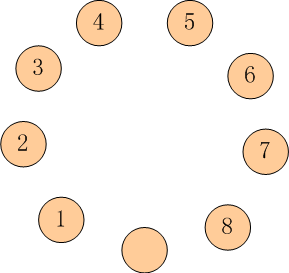
我们把这些蚱蜢顺时针编号为 1~8。每只蚱蜢都可以跳到相邻的空盘中，也可以再用点力，越过一个相邻的蚱蜢跳到空盘中。
请你计算一下，如果要使得蚱蜢们的队形改为按照逆时针排列，并且保持空盘的位置不变（也就是1-8换位，2-7换位,...），至少要经过多少次跳跃？

思路：多动不如一动，考虑空盘子在动，

盘子的状态使用数字表示，数字有很多，9*8*7*6*5*4*3*2*1种排列情况，但是使用数字直接表示需要更多的数据内存，会报错，使用map完成映射，缩小数组元素个数；其余就是bfs常规部分，代码如下，

#include<stdio.h>
#include <map>
#include <iostream>
#include <algorithm>
#define MAXSIZE 654321

struct point {
	int x[10];
};
#define MAXNUM 9
int que[MAXSIZE];
int flag[MAXSIZE];//记录是否走过  

using namespace std;
map<int,int> mp;

int main() {

	int rear = 0;
	int front = 0;
	struct point init;
	for (int i = 0; i < MAXNUM; i++) {
		init.x[i] = i;
	}
	struct point expo;
	expo.x[MAXNUM-1] = 1;
	for (int i = MAXNUM-2; i >= 0; i--) {
		expo.x[i] = expo.x[i+1] * 10;
	}
	int flagNum = 0;
	for (int i = 0; i < MAXNUM; i++) {
		flagNum += i * expo.x[i];
	}
	int endNum = 0;
	for (int i = 0; i < MAXNUM; i++) {
		endNum += i * expo.x[MAXNUM-i];
	}

	//实现映射
	//87654321->8*7*6*5*4*3*2*1
	int a[MAXNUM];
	for (int i = 0; i < MAXNUM; i++) {
		a[i] = i;
	}
	int mulRes = 1;
	int uppernum = MAXNUM;
	//printf("%d\n", uppernum);
	for (int i = 1; i <= uppernum; i++)
		mulRes = mulRes * i;
	//printf("%d", mulRes);
	for (int i = 0; i < mulRes; i++) {
		int sum = 0;
		for (int j = 0; j < MAXNUM; j++)
			sum += a[j] * expo.x[j];
		mp[sum] = i;
		next_permutation(a, a + MAXNUM);
	}


	//队列操作
	que[0] = flagNum;
	rear++;
	flag[mp[flagNum]] = 1;//标记 
	int cnt = 0;
	while (1) {
		//87654321--9
		if (flag[mp[endNum]] == 1) {
			printf("%d\n", cnt);
			break;
		}
		else {
			cnt++;
			int front_ = front;
			int rear_ = rear;
			for (int i = front_; i != rear_; i++) {
				int tempPointNum = que[i];
				//printf("%d\n", tempPointNum);
				struct point pointNow;
				int pos0;
				//数字转换为数组 
				for (int j = 0; j < MAXNUM; j++) {
					//printf("%d %d\n", j, tempPointNum / expo.x[j]);
					pointNow.x[j] = tempPointNum / expo.x[j];
					if (pointNow.x[j] == 0)pos0 = j;//找到位置 
					tempPointNum= tempPointNum- pointNow.x[j]* expo.x[j];
				}

				//数组变换，得到新的数
				int nextOp[4] = { 1,-1,2,-2 };
				for (int transi = 0; transi < 4; transi++) {
					//struct point pointNow;
					int trans2 = (pos0 + nextOp[transi] + MAXNUM) % MAXNUM;
					int arr2num = 0;
					for (int numi = 0; numi < MAXNUM; numi++) {
						if (numi == trans2) {
							arr2num += pointNow.x[pos0] * expo.x[numi];
							continue;
						}
						if (numi == pos0) {
							arr2num += pointNow.x[trans2] * expo.x[numi];
							continue;
						}
						arr2num += pointNow.x[numi] * expo.x[numi];
					}

					if (flag[mp[arr2num]] == 0) {
						que[rear] = arr2num;
						rear++;//入队 
						flag[mp[arr2num]] = 1;
					}
				}
				front++;//出队 
			}
		}
	}


	return 0;
}