在介绍门控循环神经网络之前,先简单介绍循环神经网络的基本计算方式:
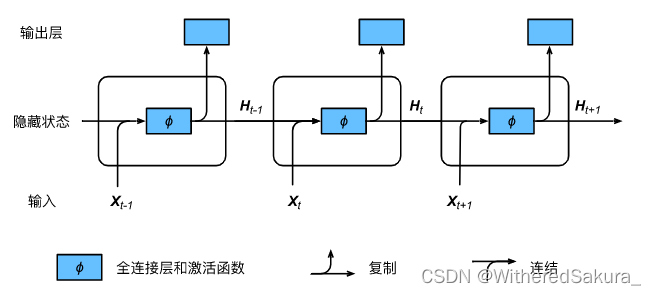
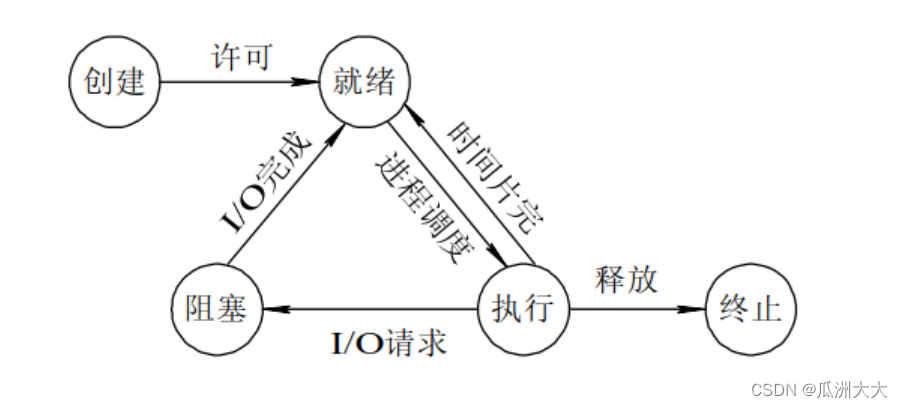
循环神经网络之称之为“循环”,因为其隐藏状态是循环利用的:
上一次输入计算出的隐藏状态与当前的输入结合,得到当前隐藏状态。
cur_output, cur_state = rnn(cur_X, last_state)
隐状态中保留了之前输入的特征和结构(对应句子的词元和结构)。
接下来介绍门控循环神经网络的几个方面:功能、计算方式、完整实现
(一)门控循环神经网络的功能:
门控循环神经网络和常规的循环神经网络有什么不同呢?
门控循环神经网络相比于常规的循环神经网络,可以有选择性地保留词元间的长期依赖关系。
这种描述或许有点抽象,所以我们通过两种不同的情况来理解一下其含义:
<1> 当早期的观测值对于接下来的观测具有重要意义时:
举一个具体的例子,当你看一篇文章或者一个句子,开头给出了时间或者地点,这个预测信息可能会影响到之后所有的观测值。
如果小说开头交代了一个年代信息,那么之后的事件都会发生在这个年代,不会出现这个年代不该出现的东西。
这时长期依赖关系对于我们的预测有着重要意义,所以应该选择性加以保留。
<2> 当一些观测值与我们接下来的观测没有联系时:
同样是一篇小说,我们不能根据它描述的一个人的发色来判断这个人的心情。
这时长期依赖关系对于我们的观测没有意义,应该选择性加以丢弃。
(二)门控循环神经网络的计算方式:
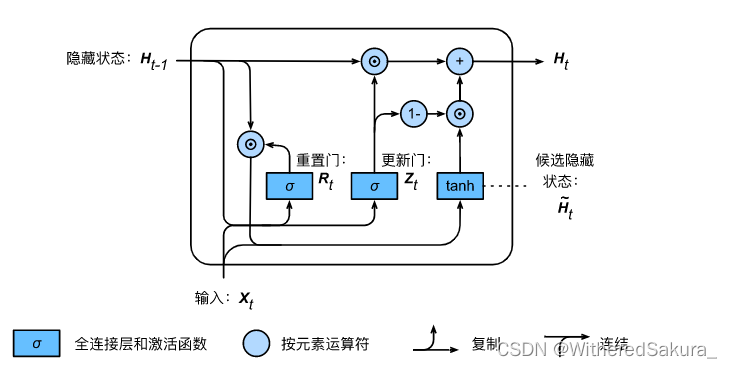
我们把门控循环神经网络的计算方式分为三步:
第一步:由cur_X和last_state计算得到重置门和更新门:
门控循环神经网络有两种门:重置门和更新门。
重置门负责的是如何将过去的信息与新的输入相结合,保留可能还想留下的旧记忆。(之所以是可能,是因为是否保留还取决于更新门)
它有助于捕获短期依赖关系。
更新门负责帮助模型决定到底传递多少过去的信息到未来,也就是更新记忆。
它有助于捕获长期依赖关系。
这两项作用分别在第二步和第三步中有所体现。
我们先来看看第一步的更新方式:
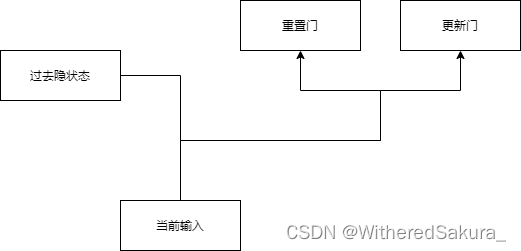
然后是计算代码:
Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z) # 更新门
R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r) # 重置门
其中W_xz, W_hz, b_z与W_xr, W_hr, b_r分别是更新门和重置门的可学习参数。
(2)第二步:用重置门去结合过去的隐状态与新的输入
还是先来看一下更新方式:
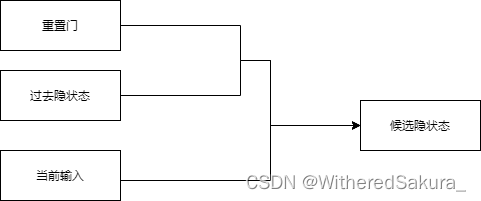
然后是计算代码:
H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h) # 候选隐状态
其中W_xh, W_hh, b_h是候选隐状态的可学习参数
(3)第三步:用更新门获取当前隐状态
先来看一下第三步的更新方式:
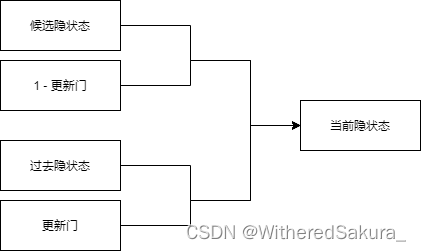
然后是计算代码:
cur_state = Z * H + (1 - Z) * H_tilda # 更新
最后我们就可以根据得到的隐状态计算输出了:
cur_output = H @ W_ho + b_o # 输出
其中W_ho, b_o是输出的可学习参数
(三)门控循环神经网络的完整实现:
import torch
class GRU:
def __init__(self, vocab_size, hidden_size, device):
self.vocab_size = vocab_size
self.hidden_size = hidden_size
self.device = device
self.parameters = self.get_params()
def get_params(self):
"""获取参数"""
num_inputs = num_outputs = self.vocab_size
def normal(shape):
return torch.randn(size=shape, device=self.device)
def three():
return (
normal((num_inputs, self.hidden_size)), # 输入参数
normal((self.hidden_size, self.hidden_size)), # 隐状态参数
torch.zeros(self.hidden_size, device=self.device) # 偏移量
)
W_xz, W_hz, b_z = three() # 更新门(z)参数(x, h, b)
W_xr, W_hr, b_r = three() # 重置门(r)参数(x, h, b)
W_xh, W_hh, b_h = three() # 候选隐状态(h)参数(x, h, b)
W_ho, b_o = normal((self.hidden_size, num_outputs)),\
torch.zeros(num_outputs, device=self.device) # 输出(o)参数(h, b)
# 附加梯度
params = [W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_ho, b_o]
for param in params:
param.requires_grad_(True)
return params
def init_state(batch_size, num_hiddens, device):
"""初始化隐状态"""
return torch.zeros((batch_size, num_hiddens), device=device)
def __call__(inputs, state, params):
W_xz, W_hz, b_z, W_xr, W_hr, b_r, W_xh, W_hh, b_h, W_ho, b_o = params
H = state
outputs = []
for X in inputs: # 输入为独热编码
Z = torch.sigmoid((X @ W_xz) + (H @ W_hz) + b_z) # 更新门
R = torch.sigmoid((X @ W_xr) + (H @ W_hr) + b_r) # 重置门
H_tilda = torch.tanh((X @ W_xh) + ((R * H) @ W_hh) + b_h) # 候选隐状态
H = Z * H + (1 - Z) * H_tilda # 更新
Y = H @ W_ho + b_o # 输出
outputs.append(Y)
return torch.cat(outputs, dim=0), H # 返回输出和更新后的隐状态
到这里门控循环神经网络的介绍就结束了,我们这里给出门控神经网络的简洁实现:
循环神经网络层的实现:
rnn = torch.nn.GRU(input_size, hidden_size, layers, dropout=dropout)
其中input_size是输入特征维度,hidden_size是隐藏层维度,layers是循环网络层数,dropout是暂退层超参数