熵及熵在机器学习中的作用
熵
reference:https://blog.csdn.net/tsyccnh/article/details/79163834
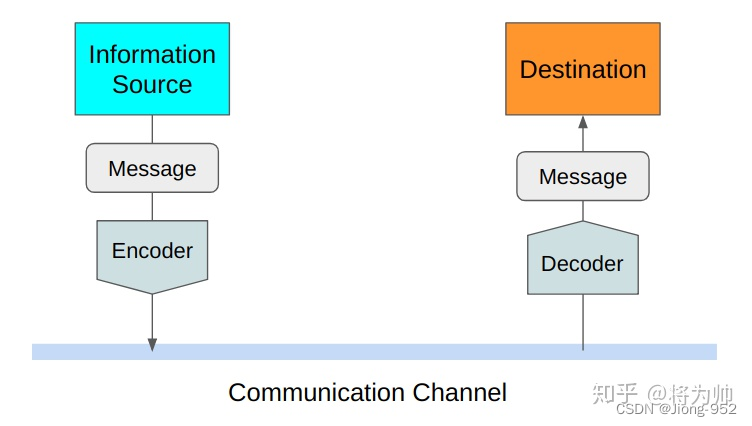
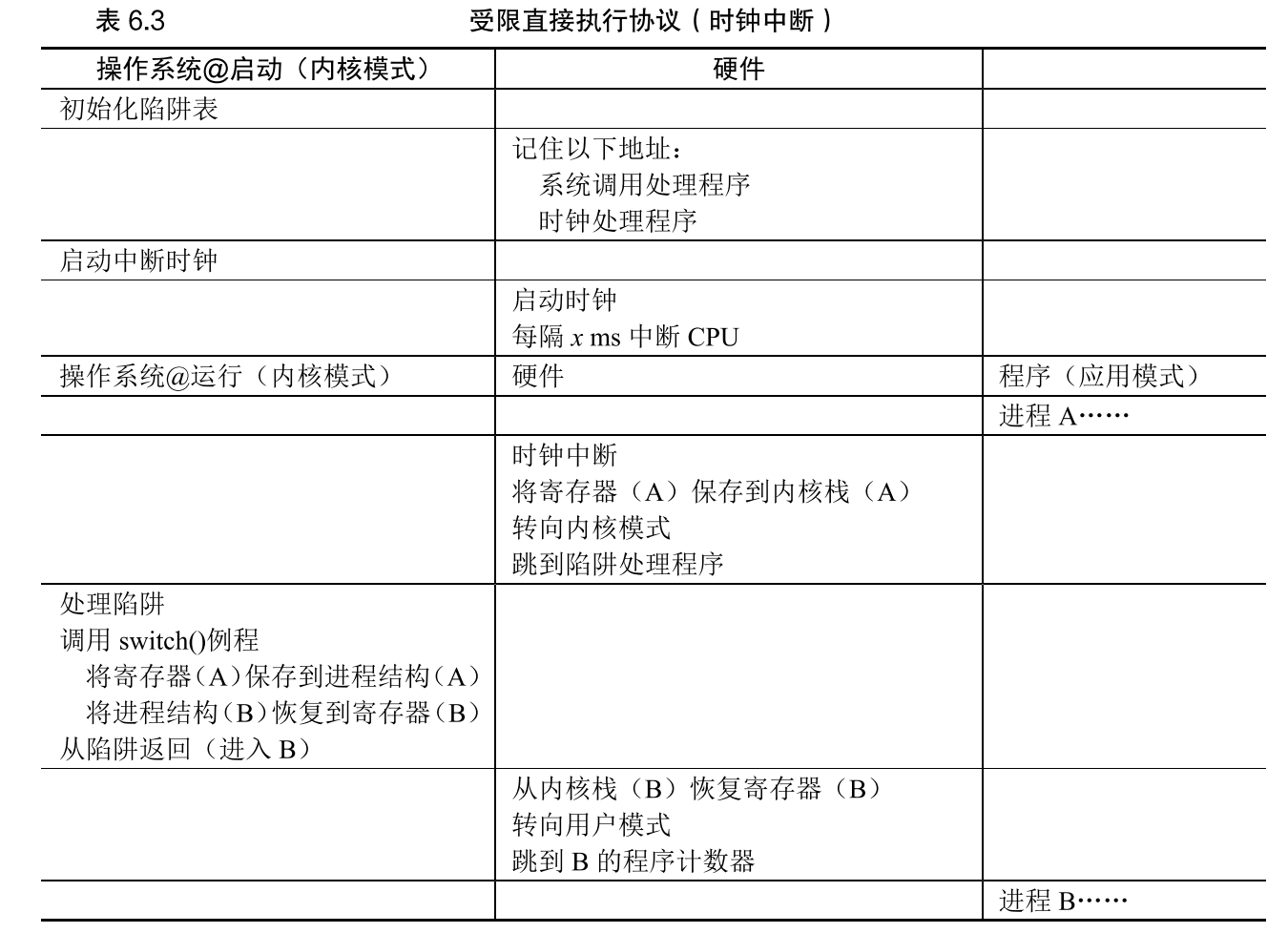
香农给熵的定义:无损编码事件信息的最小平均编码长度
直观理解熵的定义:表示某一件事的不确定性
I
(
x
0
)
=
−
l
o
g
(
p
(
x
0
)
)
I(x_0)=-log(p(x_0))
I(x0)=−log(p(x0))
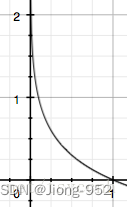
通常会用-log(x)函数来表示信息量,当概率趋近于1时,表示越确定,那么信息量接近于0,如下图所示
熵用于表示信息量的期望
H
(
X
)
=
−
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
)
H(X)=-\sum_{i=1}^n p(x_i)log(p(x_i))
H(X)=−i=1∑np(xi)log(p(xi))
相对熵
相对熵听得比较少,但是如果提到KL散度(Kullback-Leibler (KL) divergence)应该就比较常见(强化学习常客),KL散度可以用于衡量两个分布的差异性
在机器学习中,P往往用来表示样本的真实分布,Q用来表示模型所预测的分布。我们希望训练到最后Q越来越接近于P,即P与Q的KL散度越来越小。
KL散度的计算公式:
D
K
L
(
p
∣
∣
q
)
=
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
q
(
x
i
)
)
D_{KL}(p||q)=\sum\limits_{i=1}^n p(x_i)log(\dfrac{p(x_i)}{q(x_i)})
DKL(p∣∣q)=i=1∑np(xi)log(q(xi)p(xi))
n是样本数量
交叉熵
交叉熵这个概念如果单独看会很迷糊,但是从KL散度出发看就很清晰了
对上文中的KL散度展开可以得到
D
K
L
(
p
∣
∣
q
)
=
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
)
−
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
q
(
x
i
)
)
=
−
H
(
p
(
x
)
)
+
[
−
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
q
(
x
i
)
]
\begin{aligned}D_{KL}(p||q)&=\sum_{i=1}^{n}p(x_i)log(p(x_i))-\sum_{i=1}^n p(x_i)log(q(x_i))\\ &=-H(p(x))+\lbrack-\sum\limits_{i=1}^{n}{p(x_i)}log(q(x_i)\rbrack\end{aligned}
DKL(p∣∣q)=i=1∑np(xi)log(p(xi))−i=1∑np(xi)log(q(xi))=−H(p(x))+[−i=1∑np(xi)log(q(xi)]
前一部分就是P的熵,后一部分就是交叉熵。因为H§是不变的,因此我们只需要关注交叉熵就可以,这就是为什么ML习惯将交叉熵作为loss
贝叶斯、似然
参考:
-
https://blog.csdn.net/u011508640/article/details/72815981
-
http://mindhacks.cn/2008/09/21/the-magical-bayesian-method/
首先明确一个重要的概念,什么是概率,什么是统计
- 概率:已知模型(分布),求样本点x出现的概率
- 统计:已知数据,推测模型以及参数
接下来明确另一个概念,概率函数和似然函数,这两个函数都可以表示为 p ( x , θ ) p(x,\theta) p(x,θ)
- 概率函数:已知 θ \theta θ,求x样本出现的概率
- 似然函数:已知 x x x数据,似然表示对于不同的参数 θ \theta θ,x出现的概率
接下来用一个经典例子来解释极大似然估计(Maximum likelihood estimation,MLE)
极大似然估计
假如有一个罐子,里面有黑白两种颜色的球,数目多少不知,两种颜色的比例也不知。我们想知道罐中白球和黑球的比例,但我们不能把罐中的球全部拿出来数。那应该怎么办呢?很简单,前面提到了可以通过采样数据来求得模型参数。我们可以每次任意从已经摇匀的罐中拿一个球出来(采样),记录球的颜色,然后把拿出来的球再放回罐中。这个过程可以重复,我们可以用记录的球的颜色来估计罐中黑白球的比例。假如在前面的一百次重复记录中,有七十次是白球,请问罐中白球所占的比例最有可能是多少?
我们假设白球的比例为p,那么黑球的比例就是(1-p),假设模型的参数为 θ \theta θ
上面事件发生的似然函数可以表示为:
P
(
x
∣
θ
)
=
P
(
x
1
,
x
2
,
.
.
.
,
x
100
∣
θ
)
=
P
(
x
1
∣
θ
)
P
(
x
2
∣
θ
)
.
.
.
P
(
x
100
∣
θ
)
=
p
70
(
1
−
p
)
30
P(x|\theta) = P(x1,x2,...,x100|\theta) \\ = P(x1|\theta)P(x2|\theta)...P(x100|\theta) \\ =p^{70} (1-p)^{30}
P(x∣θ)=P(x1,x2,...,x100∣θ)=P(x1∣θ)P(x2∣θ)...P(x100∣θ)=p70(1−p)30
极大似然的思想就是,事件已经发生,那么我们就求让这个事件发生概率最大的模型参数,使得上面似然最大,那就是求个导,就可以,求得p = 70%
以上思想就是统计学派的思想
但是,贝叶斯学派不认可,他们认为一个事件发生,存在一个先验概率 p ( θ ) p(\theta) p(θ) ,例如,我们直观的认为硬币正反两面发生的概率都是0.5,这就是先验概率
极大后验概率估计
利用贝叶斯思想来求模型参数称为极大后验概率估计,首先给出贝叶斯公式
P
(
A
∣
B
)
=
P
(
B
∣
A
)
P
(
A
)
P
(
B
)
\mathrm{P}(\mathrm{A} \mid \mathrm{B})=\frac{\mathrm{P}(\mathrm{B} \mid \mathrm{A}) \mathrm{P}(\mathrm{A})}{\mathrm{P}(\mathrm{B})}
P(A∣B)=P(B)P(B∣A)P(A)
直接看公式很难理解对吧,下面我们一步步拆解这个公式
我们先把A换成
θ
\theta
θ,然后把B换成
x
x
x,那么上面公式可以变为
P
(
θ
∣
x
)
=
P
(
x
∣
θ
)
P
(
θ
)
P
(
x
)
\mathrm{P}(\theta \mid x) = \frac{\mathrm{P}(x \mid \theta) \mathrm{P}(\theta)}{\mathrm{P}(x)}
P(θ∣x)=P(x)P(x∣θ)P(θ)
现在我们再来看这个公式,我们可以惊奇的发现
P
(
x
∣
θ
)
P(x|\theta)
P(x∣θ)不就是我们前面提到的似然函数吗,而
P
(
θ
)
P(\theta)
P(θ)表示先验概率,即我们基于经验得到的先验知识,
P
(
x
)
P(x)
P(x)是客观事实数据,是一个已知的值。而
P
(
θ
∣
x
)
P(\theta|x)
P(θ∣x)表示后验概率,即我们最大化的函数。
关于 P ( x ) P(x) P(x),我们可以从实验数据得到这个值,例如我们每一次实验都是投10个硬币,总共做了1000次实验,某一个路径“反正正正正反正正正反”出现了n次,则 P ( x 0 ) = n / 1000 P(x_0) = n / 1000 P(x0)=n/1000,总之这个数据不影响我们对于后验概率的计算,所以 P ( θ ∣ x ) ∝ P ( x ∣ θ ) P ( θ ) \mathrm{P}(\theta \mid x) \propto \mathrm{P}(x \mid \theta) \mathrm{P}(\theta) P(θ∣x)∝P(x∣θ)P(θ) 中间符号表示正比于
贝叶斯拓展
- https://www.youtube.com/watch?v=-1dYY43DRMA
可以将贝叶斯的公式看成是我们人类的学习过程, P ( θ ) {P}(\theta) P(θ)是我们对某件事发生的先验概率, P ( x ∣ θ ) \mathrm{P}(x \mid \theta) P(x∣θ)是我们在生活中学习观察到数据后的似然,我们就是使用似然来更新对某件事的认知。