前言:我们都熟知高精度的加减法可以用字符串来模拟实现,其实乘除法的高精度计算也和加减法类似却也略有不同,下面我们一起来看一下高精度的乘除法的模拟实现,希望可以帮助到大家。

目录
1.高精度乘法的实现
1.1原理重点难点解析
1.2代码实现
2.高精度除法的实现
2.1原理思路描述
2.2 代码实现
3.金句省身
1.高精度乘法的实现
1.1原理重点难点解析
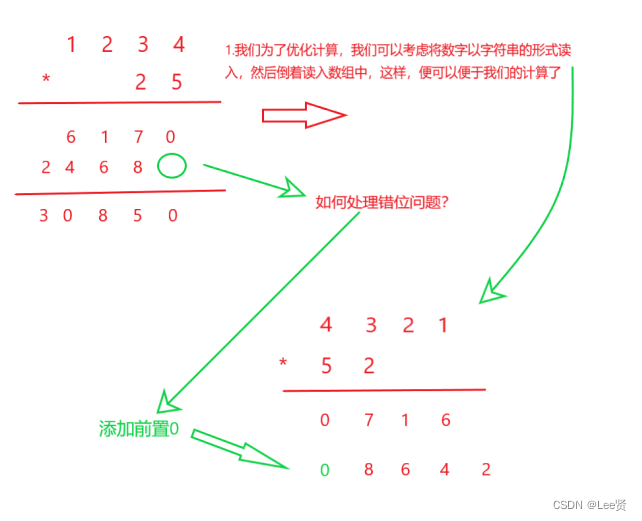
原理上并不难,主要还是要注意代码实现的细节问题:
1.2代码实现
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll maxsize = 0;//用于记录最长的乘积位数
vector<vector<int>> mul(vector<int>& A, vector<int>& B)
{
vector<vector<int>>ans;
for (int i = 0; i < B.size(); i++)
{
vector<int> temp;
for (int k = 0; k < i; k++)
temp.push_back(0);
int jinwei = 0;
for (int j = 0; j < A.size(); j++)
{
jinwei += A[j] * B[i];
temp.push_back(jinwei % 10);
jinwei /= 10;
}
if (jinwei)
temp.push_back(jinwei);
ans.push_back(temp);
maxsize = max(maxsize, (ll)temp.size());
/*for (int l = temp.size()-1; l>=0; l--)
cout << temp[l] << " ";
cout << endl;
*/
temp.clear();
}
return ans;
}
vector<int> add(vector<vector<int>>& ans)
{
vector<int> cot;
int jinwei = 0;
for (ll j = 0; j < maxsize||jinwei; j++)//最后一次进位有效时仍旧可以进入循环
{
for (int i = 0; i < ans.size(); i++)
{
if (j < ans[i].size())
jinwei += ans[i][j];
}
cot.push_back(jinwei % 10);
jinwei /= 10;
}
return cot;
}
int main()
{
string s1, s2;
cin >> s1 >> s2;
if(s1=="0"||s2=="0")
{
cout<<"0"<<endl;
return 0;
}
vector<int>a, b;
for (int i = s1.size()-1; i >= 0; i--)
a.push_back(s1[i] - '0');
for (int i = s2.size()-1; i >= 0; i--)
b.push_back(s2[i] - '0');
auto c = mul(a, b);
auto ans = add(c);
for (int i = ans.size()-1; i>=0; i--)
cout << ans[i];//结果为倒序输出的形式
cout << endl;
return 0;
}2.高精度除法的实现
2.1原理思路描述
首先,我们这里应该是以高精度除高精度为条件,高精度除低精度的可以通过“弯道”超车,这里我们不予以讨论,只是以高精度除高精度为前提下的实现方式。
1.我们可以用循环减法模拟实现除法的商的计算,当我们的被减数减去减数还大于减数时,我们就可以让我们的该位上的商加1,直到该位上对应的被减数比减数小了,循环就停下来,此时的变量的累加值就是该位对应的商的结果。

2.在存储数组的时候是采取逆序还是正序存储呢,这里我用的是逆序存储,两者的区别在于,逆序存储时方便减法的计算,正序存储时方便除法的计算,其实除法的计算也包括了减法的计算,所以还是让减法运算更方便为好。
减法操作函数

3.如果我们的输入出现被除数比除数小的情况怎么办?
这个时候我们可以将其当做特殊情况进行处理即可,因为这种情况返回的结果不想要计算,直接返回被除数就好,商就是0了。

剩下的就没什么难点了,重点是有很多的细节问题,我们在可以在心里模拟这个过程,包括移位啊,将被除数的下一位落下来等操作,都体现在代码中了,我也是改了很久并用一些注释标出加以解释,希望可以帮助你更好的理解高精度除法的相关实现及其细节问题。
2.2 代码实现
#include <bits/stdc++.h>
using namespace std;
bool cmp(vector<int>& A, vector<int>& B) //数组比较函数,目的是比较被除数和除数的大小
{
if (A.size() != B.size()) return A.size() > B.size();
for (int i = A.size() - 1; i >= 0; i--) {
if (A[i] != B[i]) return A[i] > B[i];
}
return true;
}
vector<int> sub(vector<int>& A, vector<int>& B) //减法函数,模拟进行除法商的计算,倒序存储数字也是为了方便进行减法计算
{
vector<int> C;
int t = 0;
for (int i = 0; i < A.size() || t; i++) {
t = A[i] - t;
if (i < B.size()) t -= B[i];
C.push_back((t + 10) % 10);//加10起到了t小于0时可以进行进位操作
if (t < 0) t = 1;
else t = 0;
}
while (C.size() > 1 && C.back() == 0) C.pop_back();//去除前导0
return C;
}
vector<int> div(vector<int>& A, vector<int>& B, vector<int>& r)
{
vector<int> C; //存储的是倒序的商数组
//如果被除数比除数还小,那么直接返回0和被除数即可
if (A.size() < B.size())
{
r = A;//一定注意余数是A不是B
reverse(r.begin(), r.end());
C.push_back(0);
return C;
}
//注意我们的r数组此时一直处于倒序的状态
int j = B.size();
r.assign(max(A.begin(),A.end() - j), A.end());//有可能也会是小数除大数
while (j <= A.size())
{
int k = 0;
while (cmp(r, B))
{
vector<int> s = sub(r, B); //减法模拟除法
r.clear();
r.assign(s.begin(), s.end());//注意此时r数组还是倒序的
k++;
}
C.push_back(k);//将商放入数组
if (j < A.size())
r.insert(r.begin(), A[A.size() - j - 1]);//再往后拿被除数一位和除数相除
if (r.size() > 1 && r.back() == 0)
r.pop_back();//去除前导0,注意此时r数组还是倒序的,高位存储在末尾
j++;
}
//reverse(C.begin(), C.end());
while (C.size() > 1 && *(C.begin()) == 0) C.erase(C.begin());//去除前导0
return C;
}
int main()
{
string s1, s2;
cin >> s1 >> s2;
vector<int> a, b,r;//r表示余数,c表示商数组
for (int i = s1.size()-1; i >=0; i--)//将数字逆序存入数组中
a.push_back(s1[i] - '0');
for (int i = s2.size()-1; i>=0; i--)
b.push_back(s2[i] - '0');
auto c = div(a, b, r);
for (int i = 0; i < c.size(); i++)
cout << c[i];
cout << endl;
for (int i = r.size()-1; i>=0; i--)
cout << r[i];
cout << endl;
return 0;
}3.金句省身
我永远喜欢那些优秀又谦逊的人,他们明明拥有吊打所有人的能力,却又毫无优越感,对人温和的就像傍晚的风,工作上坚定有主见,与人相处时又温和自谦。
如果恰好喜欢的人也很优秀,那就狠狠的把自己变得优秀,无限去接近。别去害怕,也别去自卑,而是要尽快让你的能力跟得上你的眼光。当你足够优秀,才能散发光芒,自然有同样优秀的人追着光向你走来。