范例题目：
建立一个逻辑回归模型预测一个学生是否通过研究生入学考试。N表示训练集中学生个数，Score1、Score2、 Score3、 Score4是N维数组，分别表示N个学生研究生初试、专业课复试、英语面试成绩、专业课面试成绩。Admitted是N维{0,1}数组，1代表被录取，0代表未被录取。给出逻辑回归的参数结构、初始化过程、损失函数（经验风险）设置，基于随机梯度下降和梯度下降的参数学习过程。

数学推导

逻辑回归是一种二元分类算法，可以用于预测一个学生是否通过研究生入学考试。以下是逻辑回归模型的参数结构和学习过程。

参数结构：
逻辑回归模型的参数结构包括权重向量 $w$ 和偏置 $b$。对于一个具有 $n$ 个特征的样本 $x=(x_1,x_2,...,x_n)$，模型的预测输出 $y$ 可以表示为：
$$y=\sigma (w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b)$$
其中，$\sigma (x)$ 是sigmoid函数，可以将任意实数映射到区间 $(0,1)$ 上，定义为：
$$\sigma (x)=\frac{1}{1+e^{-x}}$$
初始化过程：
为了学习逻辑回归模型的参数 $w$ 和 $b$，需要对它们进行初始化。常见的初始化方法是将 $w$ 初始化为0向量，$b$ 初始化为0标量。

损失函数（经验风险）设置：
逻辑回归模型的损失函数通常采用交叉熵损失函数。对于一个样本 $(x,y)$，其交叉熵损失函数可以表示为：
$$J(w,b)=-\left(y\log \left(\hat{y}\right)+(1-y)\log \left(1-\hat{y}\right)\right)$$
其中，$\hat{y}=\sigma (w_1{x}_1+w_2{x}_2+...+w_n{x}_n+b)$ 是模型的预测输出，$y$ 是样本的真实标签。

基于随机梯度下降的参数学习过程：
在基于随机梯度下降的参数学习过程中，模型每次随机选取一个样本 $(x^{(i)},y^{(i)})$ 进行训练。算法的更新过程如下：
$$w_j\leftarrow w_j-\alpha \frac{\partial J}{\partial w_j}=w_j+\alpha (y^{(i)}-{\hat{y}}^{(i)})x_j^{(i)}$$$$b\leftarrow b-\alpha \frac{\partial J}{\partial b}=b+\alpha (y^{(i)}-{\hat{y}}^{(i)})$$
其中，$\alpha$ 是学习率，${\hat{y}}^{(i)}=\sigma (w_1{x}_1^{(i)}+w_2{x}_2^{(i)}+...+w_n{x}_n^{(i)}+b)$ 是模型对样本 $x^{(i)}$ 的预测输出。

基于梯度下降的参数学习过程：
在基于梯度下降的参数学习过程中，模型在每一轮迭代中使用整个训练集进行训练。算法的更新过程如下：
$$b\leftarrow b-\alpha \frac{1}{N}\sum _{i=1}^N(y^{(i)}-{\hat{y}}^{(i)})$$
其中，$\alpha$ 是学习率，$N$ 是训练集中样本的个数，${\hat{y}}^{(i)}=\sigma (w_1{x}_1^{(i)}+w_2{x}_2^{(i)}+...+w_n{x}_n^{(i)}+b)$ 是模型对样本 $x^{(i)}$ 的预测输出。

以上是逻辑回归模型的参数结构、初始化过程、损失函数设置，以及基于随机梯度下降和梯度下降的参数学习过程。在实际应用中，可以根据具体情况调整学习率和训练轮数等超参数，以获得更好的模型性能。

代码实现

代码基于torch实现，其中注释详尽，自行查阅
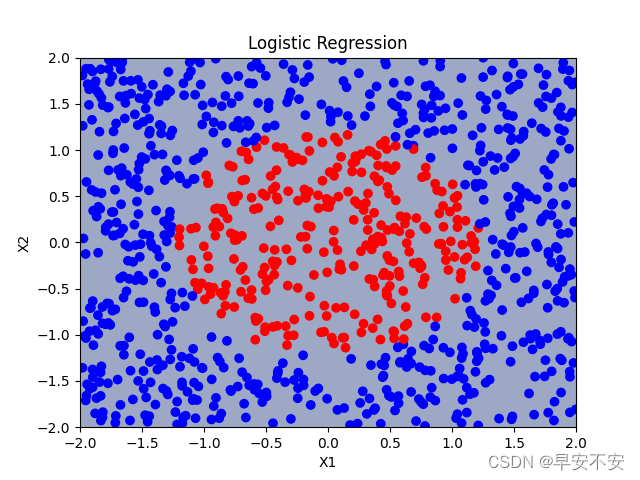
以下代码首先定义了一个逻辑回归模型类 LogisticRegression，包含一个全连接层和一个 Sigmoid 激活函数。训练函数 train 使用随机梯度下降优化器和二元交叉熵损失函数对模型进行训练，最后测试模型的准确率，并进行了简易的可视化。

import torch
import torch.nn as nn
import numpy as np
import matplotlib.pyplot as plt

# 定义逻辑回归模型类
class LogisticRegression(nn.Module):
    def __init__(self, num_features):
        super(LogisticRegression, self).__init__()
        self.linear = nn.Linear(num_features, 1)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        out = self.linear(x)
        out = self.sigmoid(out)
        return out

# 训练函数
def train(X, y, model, learning_rate, num_epochs, batch_size):
    criterion = nn.BCELoss() # 二元交叉熵损失函数
    optimizer = torch.optim.SGD(model.parameters(), lr=learning_rate) # 随机梯度下降优化器

    dataset = torch.utils.data.TensorDataset(X, y)
    dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)

    for epoch in range(num_epochs):
        for inputs, targets in dataloader:
            # 前向传播
            outputs = model(inputs)

            # 计算损失函数值并反向传播
            loss = criterion(outputs, targets)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

        if (epoch+1) % 100 == 0:
            print('Epoch [{}/{}], Loss: {:.4f}'.format(epoch+1, num_epochs, loss.item()))

# 数据准备
np.random.seed(42)
N = 1000
X = np.random.rand(N, 2) * 4 - 2
y = np.zeros((N, 1))
y[np.sum(X ** 2, axis=1) <= 1.5] = 1
X = torch.from_numpy(X).float()
y = torch.from_numpy(y).float()

# 定义模型和超参数
num_features = 2
learning_rate = 1e-4
num_epochs = 1000
batch_size = 10
model = LogisticRegression(num_features)

# 模型训练
train(X, y, model, learning_rate, num_epochs, batch_size)

# 绘制决策边界和数据点
with torch.no_grad():
    X_grid = np.meshgrid(np.linspace(-2, 2, 100), np.linspace(-2, 2, 100))
    X_test = torch.from_numpy(np.array([X_grid[0].ravel(), X_grid[1].ravel()]).T).float()
    y_pred = model(X_test).detach().numpy().reshape(X_grid[0].shape)
    y_pred = np.where(y_pred >= 0.5, 1, 0)

    outputs = model(X)
    predicted = (outputs >= 0.5).float()
    accuracy = (predicted == y).float().mean()
    print('Accuracy: {:.2f}%'.format(accuracy.item() * 100))

plt.contourf(X_grid[0], X_grid[1], y_pred, alpha=0.5)
plt.scatter(X[:, 0], X[:, 1], c=y[:, 0], cmap='bwr')
plt.title('Logistic Regression')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()